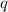 und der Masse
und der Masse 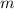 im Magnetfeld
im Magnetfeld 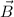 kennengelernt. Sie lautet (siehe
Gl. (12.15))
kennengelernt. Sie lautet (siehe
Gl. (12.15))
In Abschnitt 12.3 haben wir die Hamilton-Funktion für ein Teilchen der Ladung
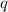 und der Masse
und der Masse 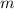 im Magnetfeld
im Magnetfeld 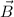 kennengelernt. Sie lautet (siehe
Gl. (12.15))
kennengelernt. Sie lautet (siehe
Gl. (12.15))
Wir geben in diesem Kapitel eine Motivation dieser Hamilton-Funktion, indem wir die erweiterte Hamilton-Funktion
für ein Teilchen der Ladung 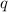 und der Masse
und der Masse 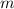 im elektromagnetischen Feld,
welches durch die elektrische Feldstärke
im elektromagnetischen Feld,
welches durch die elektrische Feldstärke 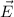 und die magnetische Flussdichte
und die magnetische Flussdichte 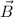 charakterisiert ist, auf die bekannte Newtonsche Bewegungsgleichung
charakterisiert ist, auf die bekannte Newtonsche Bewegungsgleichung
zurückführen. Dabei ist 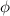 das elektrische Potential und es gelten zwischen der
elektrischen Feldstärke
das elektrische Potential und es gelten zwischen der
elektrischen Feldstärke 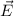 , der magnetische Flussdichte
, der magnetische Flussdichte 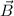 , dem elektrischen
Potential
, dem elektrischen
Potential 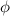 und dem Vektorpotential
und dem Vektorpotential 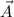 die folgenden Zusammenhänge
die folgenden Zusammenhänge
Wir beginnen mit der Aufstellung der Hamiltonschen Bewegungsgleichungen
wobei 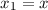 ,
, 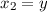 ,
, 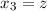 . Aus (J.6) ergibt sich für die zweite Ableitung von
. Aus (J.6) ergibt sich für die zweite Ableitung von
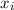 nach der Zeit
nach der Zeit
Damit erhalten wir
Mit der Vektoridentität
ergibt sich
und damit
Somit haben wir die Hamilton-Funktion (J.2) auf die Newtonsche Bewegungsgleichung (J.3) zurückgeführt.