In diesem Kapitel befassen wir uns mit dem Einfluss eines externen Magnetfelds auf
das Spektrum eines Atoms. Wir werden sehen, dass infolge dieser Beeinflussung die
Entartung der Energieniveaus teilweise aufgehoben wird und als Folge davon die
einzelnen Spektrallinien in mehrere Linien aufgespaltet werden. Dieser Effekt wird
nach seinem Entdecker Pieter Zeeman Zeeman-Effekt genannt. 1902 erhielt er für
diese Entdeckung gemeinsam mit Hendrik Antoon Lorentz den Nobelpreis in
Physik.
Wir beginnen mit ein paar historischen Bemerkungen zur Entdeckung des
Zeeman-Effekts. Anschliessend beschränken wir uns auf das Wasserstoffatom und
betrachten ein semiklassisches Modell zur Beschreibung des Effekts, gefolgt von
einer quantenmechanischen Behandlung. Am Ende des Kapitels steht die
Zusammenfassung der Resultate und die Betrachtung des Zeeman-Effekts für das
Spektrum des Wasserstoffatoms.
Im Jahr 1862, also 25 Jahre vor der Entdeckung des Elektrons, untersuchte Michael Faraday in
einem Experiment
die folgende Frage: Welchen Einfluss hat ein äusseres Magnetfeld auf das
Linienspektrum, das von Gasflammen, die durch Alkali- und andere Salze
gefärbt werden, emittiert wird? Das Auflösungsvermögen seines einfachen
Prismenspektroskops genügte jedoch nicht, um einen Effekt zu finden.
Erst 1896 wurde das Experiment von Faraday von Zeeman wieder aufgegriffen. Mit
seiner Messapparatur konnte er eine Verbreiterung der Spektrallinien nachweisen, die
er folgendermassen deutete: Durch das äussere Magnetfeld kommt es zur Aufspaltung
der einzelnen Linien in mehrere. Er war zudem in der Lage die Grössenordnung dieser
Aufspaltung anzugeben.
Im selben Jahr
gab Lorentz eine Interpretation der Zeeman Aufspaltung. Er nahm an, dass in
Atomen Teilchen der Ladung 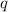 und der Masse
und der Masse 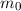 sich auf einer Kreisbahn mit
einem bestimmten Radius
sich auf einer Kreisbahn mit
einem bestimmten Radius 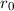 bewegen. Die Zentripetalbeschleunigung
bewegen. Die Zentripetalbeschleunigung 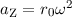 soll durch eine Zentripetalkraft
soll durch eine Zentripetalkraft 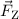 (unbekannten Ursprungs) erzeugt werden.
Befindet sich nun dieses Atom in einem homogenen Magnetfeld
(unbekannten Ursprungs) erzeugt werden.
Befindet sich nun dieses Atom in einem homogenen Magnetfeld 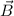 , welches
senkrecht zur Bahnrichtung der Ladung
, welches
senkrecht zur Bahnrichtung der Ladung 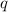 gerichtet ist, so wirkt auf diese die
Lorentz-Kraft
gerichtet ist, so wirkt auf diese die
Lorentz-Kraft 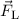 in radialer Richtung nach aussen oder nach innen abhängig
vom Umlaufsinn des Teilchens. Damit dieses auf seiner Bahn bleibt, muss
im ersten Fall die Winkelgeschwindigkeit
in radialer Richtung nach aussen oder nach innen abhängig
vom Umlaufsinn des Teilchens. Damit dieses auf seiner Bahn bleibt, muss
im ersten Fall die Winkelgeschwindigkeit 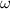 verkleinert, im zweiten Fall
vergrössert werden. Der Betrag der Lorentz-Kraft
verkleinert, im zweiten Fall
vergrössert werden. Der Betrag der Lorentz-Kraft 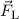 ist dabei gegeben
durch
ist dabei gegeben
durch

Es sei nun 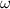 die Winkelgeschwindigkeit ohne Magnetfeld und
die Winkelgeschwindigkeit ohne Magnetfeld und 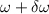 die
Winkelgeschwindigkeit mit Magnetfeld. Die durch das Magnetfeld bewirkte Änderung
die
Winkelgeschwindigkeit mit Magnetfeld. Die durch das Magnetfeld bewirkte Änderung
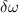 der Winkelgeschwindigkeit ergibt sich durch Gleichsetzen des Betrags
der Winkelgeschwindigkeit ergibt sich durch Gleichsetzen des Betrags 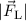 der
Lorentz-Kraft mit der Änderung der Zentripetalkraft
der
Lorentz-Kraft mit der Änderung der Zentripetalkraft 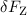 , wobei
, wobei 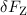 in erster
Näherung gegeben ist durch
in erster
Näherung gegeben ist durch
Gleichsetzen mit (12.1) liefert
woraus wir für die durch das Magnetfeld bewirkte Änderung 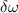 der
Winkelgeschwindigkeit das folgende Resultat erhalten
der
Winkelgeschwindigkeit das folgende Resultat erhalten
Wie wir in den folgenden Abschnitten sehen werden, stimmt dieses Resultat
mit dem semiklassischen Modell (siehe Abschnitt 12.2) und auch der rein
quantenmechanischen Herleitung (siehe Abschnitt 12.3) überein.
Diese Interpretation des Zeeman-Effekts von Lorentz steht im engen Zusammenhang
mit der Entdeckung, dass das Elektron ein Bestandteil des Atoms ist: Joseph John
Thomson bestimmte 1897 aus der Ablenkung eines Elektronenstrahls im elektrischen
und magnetischen Feld das Verhältnis von Ladung zu Masse. Er verglich sein
Ergebnis mit dem Verhältnis 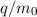 , das sich mit Hilfe der Interpretation
von Lorentz aus der experimentellen Abschätzung der Zeeman-Aufspaltung
, das sich mit Hilfe der Interpretation
von Lorentz aus der experimentellen Abschätzung der Zeeman-Aufspaltung
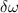 ergab und fand innerhalb der damals recht grossen Fehlerschranken
Übereinstimmung. Seit jener Zeit weiss man, dass das Elektron ein Bestandteil des
Atoms ist.
ergab und fand innerhalb der damals recht grossen Fehlerschranken
Übereinstimmung. Seit jener Zeit weiss man, dass das Elektron ein Bestandteil des
Atoms ist.
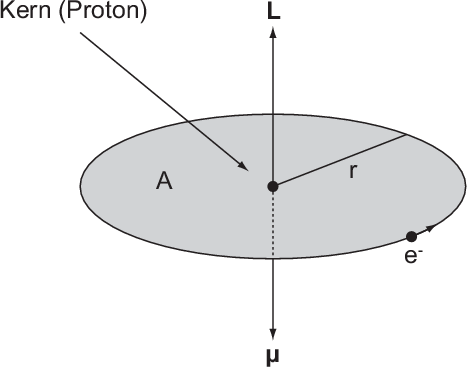
Wie in der Einleitung des Kapitels erwähnt, beschränken wir uns im Folgenden auf
die Behandlung des Wasserstoffatoms. Wir beginnen mit einer semiklassischen
Behandlung. Dabei gehen wir vom Bohrschen Atommodell (siehe Kapitel 8) aus,
indem wir annehmen, dass sich im Wasserstoffatom das negativ geladene Elektron
auf einer Kreisbahn um den positiv geladenen Kern bewegt (siehe Abb. 12.1).
Durch dieses kreisende Elektron wird ein Kreisstrom 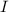 erzeugt, welcher ein
magnetisches Moment
erzeugt, welcher ein
magnetisches Moment 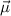 antiparallel zur Flächennormalen
antiparallel zur Flächennormalen 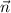 hervorruft
hervorruft
wobei 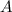 die von der Kreisbahn eingeschlossene Fläche bezeichnet. Der Strom
die von der Kreisbahn eingeschlossene Fläche bezeichnet. Der Strom 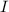 lässt sich durch die Elektronenladung
lässt sich durch die Elektronenladung 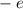 und die Umlauffrequenz
und die Umlauffrequenz  ausdrücken
und die Fläche
ausdrücken
und die Fläche 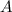 durch den Bahnradius
durch den Bahnradius  . Es ergibt sich
. Es ergibt sich
Wir vergleichen diesen Ausdruck für das magnetische Moment 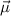 mit dem
Bahndrehimpuls
mit dem
Bahndrehimpuls 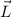 des Elektrons
des Elektrons
und erhalten
Das Verhältnis von magnetischem Moment 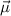 zu Bahndrehimpuls
zu Bahndrehimpuls 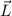 wird
gyromagnetisches Verhältnis genannt und mit
wird
gyromagnetisches Verhältnis genannt und mit 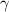 bezeichnet
bezeichnet
Das nächste Ziel ist die potentielle Energie 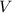 des Elektrons in einem homogenen
externen Magnetfeld
des Elektrons in einem homogenen
externen Magnetfeld 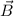 zu bestimmen. Sie ist gegeben durch
zu bestimmen. Sie ist gegeben durch
wobei 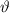 den Winkel zwischen magnetischem Moment
den Winkel zwischen magnetischem Moment 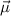 und Magnetfeld
und Magnetfeld 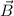 bezeichnet. Demzufolge erreicht die potentielle Energie
bezeichnet. Demzufolge erreicht die potentielle Energie 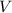 ihr Minimum für
ihr Minimum für
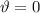 , d.h. wenn
, d.h. wenn 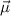 parallel zu
parallel zu 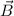 ausgerichtet ist und ihr Maximum
für
ausgerichtet ist und ihr Maximum
für 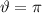 , d.h. wenn
, d.h. wenn 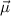 antiparallel zu
antiparallel zu 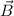 ausgerichtet ist. Mit (12.8)
erhalten wir für die potentielle Energie
ausgerichtet ist. Mit (12.8)
erhalten wir für die potentielle Energie 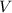 des Elektrons mit Bahndrehimpuls
des Elektrons mit Bahndrehimpuls
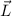
Quantenmechanisch (siehe Abschnitt 11.2) ist die z-Komponente 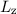 des
Bahndrehimpulses
des
Bahndrehimpulses 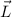 gegeben durch
gegeben durch
wobei die magnetische Quantenzahl 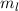 nur die diskreten Werte
nur die diskreten Werte 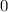 ,
,  ,
, 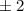 , ...
annehmen kann. Somit ergibt sich für die potentielle Energie
, ...
annehmen kann. Somit ergibt sich für die potentielle Energie 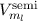 des
magnetischen Moments des Elektrons im Wasserstoffatom
des
magnetischen Moments des Elektrons im Wasserstoffatom
wobei 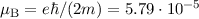 eV/T das Bohr-Magneton bezeichnet, wir
den Index
eV/T das Bohr-Magneton bezeichnet, wir
den Index 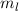 eingeführt haben und der obere Index semi andeuten soll,
dass unsere Herleitung semiklassisch erfolgte.
eingeführt haben und der obere Index semi andeuten soll,
dass unsere Herleitung semiklassisch erfolgte. 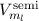 wird Zeeman-Energie
genannt. Damit ergibt sich für die Energiewerte
wird Zeeman-Energie
genannt. Damit ergibt sich für die Energiewerte 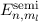 des Wasserstoffatoms
(siehe Abschnitt 11.2.3) im homogenen externen Magnetfeld
des Wasserstoffatoms
(siehe Abschnitt 11.2.3) im homogenen externen Magnetfeld 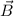 die folgende
Korrektur
die folgende
Korrektur
wobei 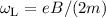 die Larmor-Frequenz bezeichnet und wir für die Energiewerte
den zusätzlichen Index
die Larmor-Frequenz bezeichnet und wir für die Energiewerte
den zusätzlichen Index 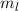 eingeführt haben. Das bedeutet, dass durch ein
homogenes externes Magnetfeld
eingeführt haben. Das bedeutet, dass durch ein
homogenes externes Magnetfeld 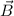 die durch die magnetische Quantenzahl
die durch die magnetische Quantenzahl 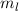 bewirkte
bewirkte 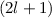 -fache Entartung der Energiewerte
-fache Entartung der Energiewerte 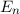 aufgehoben wird (siehe
Abb. 12.2).
aufgehoben wird (siehe
Abb. 12.2).
Die  -Niveaus (
-Niveaus (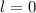 ,
, 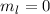 ) werden durch das Magnetfeld nicht beeinflusst.
Die
) werden durch das Magnetfeld nicht beeinflusst.
Die 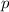 -Niveaus (
-Niveaus (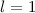 ,
, 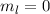 ,
,  ) werden in drei und die
) werden in drei und die 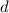 -Niveaus
(
-Niveaus
(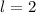 ,
, 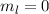 ,
,  ,
, 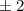 ) in fünf Niveaus mit Abstand
) in fünf Niveaus mit Abstand 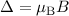 aufgespaltet.
aufgespaltet.
Wir starten mit der allgemeinen Hamilton-Funktion 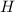 für ein Teilchen der Ladung
für ein Teilchen der Ladung
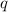 und der Masse
und der Masse 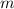 im Magnetfeld
im Magnetfeld 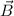 (für eine Motivation verweisen wir auf
Anhang J)
(für eine Motivation verweisen wir auf
Anhang J)
wobei 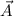 das sogenannte Vektorpotential bezeichnet. Mit
das sogenannte Vektorpotential bezeichnet. Mit 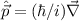 erhalten wir
für den entsprechenden Hamilton-Operator
erhalten wir
für den entsprechenden Hamilton-Operator 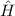 den folgenden Ausdruck
den folgenden Ausdruck
Wir verwenden nun (für die Fortsetzung des Buchs) die sogenannte
Coulomb-Eichung
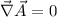 und erhalten
und erhalten
Wir kommen nun zum Spezialfall eines Elektrons (Ladung 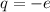 ) im homogenen
Magnetfeld
) im homogenen
Magnetfeld 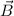 . Ohne Beschränkung der Allgemeinheit wählen wir
. Ohne Beschränkung der Allgemeinheit wählen wir 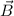 entlang der
z-Achse, d.h.
entlang der
z-Achse, d.h. 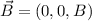 . Das entsprechende Vektorpotential
. Das entsprechende Vektorpotential 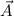 können wir
schreiben als
können wir
schreiben als
da
Einsetzen von (12.18) in (12.17) liefert für den Hamilton-Operator 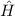 eines
Elektrons im homogenen Magnetfeld
eines
Elektrons im homogenen Magnetfeld
wobei wir im letzten Schritt benützt haben, dass 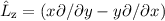 .
.
Wir vergleichen die Grössenordnungen der Terme (1) und (2) des Hamilton-Operators
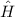 von Elektronen in Atomen. Wir benützen dazu, dass
von Elektronen in Atomen. Wir benützen dazu, dass 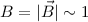 T,
T,
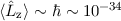 Js,
Js, 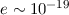 C,
C, 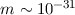 kg,
kg, 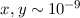 m und
erhalten
m und
erhalten
Demzufolge können wir Term (2) gegenüber Term (1) für ein Elektron in Atomen
unter dem Einfluss eines homogenen externen Magnetfelds vernachlässigen. Damit
lautet der Hamilton-Operator 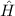 für das Wasserstoffatom im homogenen externen
Magnetfeld
für das Wasserstoffatom im homogenen externen
Magnetfeld
Nach Abschnitt 11.3 sind die Wellenfunktionen 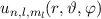 sowohl Eigenfunktionen
des Hamilton-Operators
sowohl Eigenfunktionen
des Hamilton-Operators 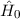 mit den Eigenwerten
mit den Eigenwerten 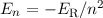 als auch des
Operators
als auch des
Operators 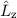 mit den Eigenwerten
mit den Eigenwerten 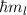 . Deshalb gilt
. Deshalb gilt
Folglich sind die Energiewerte 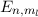 des Wasserstoffatoms im homogenen externen
Magnetfeld gegeben durch
des Wasserstoffatoms im homogenen externen
Magnetfeld gegeben durch
Dieses Resultat stimmt mit dem semiklassischen Resultat (12.14) überein.
Wir betrachten nun den Effekt eines homogenen externen Magnetfelds auf das
Spektrum des Wasserstoffatoms. Die semiklassische Behandlung (siehe Abschnitt
12.2) und die quantenmechanische Behandlung (siehe Abschnitt 12.3) haben gezeigt,
dass die Existenz eines homogenen externen Magnetfelds die Aufspaltung der
Energieniveaus des Wasserstoffatoms zur Folge hat. Diese Aufspaltung der
Energieniveaus führt zu zusätzlichen Übergängen und damit zu zusätzlichen
Spektrallinien im Spektrum des Wasserstoffatoms. Jedoch ist die Anzahl der
Übergänge durch die sogenannten Auswahlregeln (siehe Abschnitt 15.3) beschränkt.
Diese geben Auskunft, ob ein Übergang zwischen zwei Energieniveaus unter Emission
oder Absorption eines Photons möglich ist oder nicht. Beim Wasserstoffatom lauten
die Auswahlregeln: Der Übergang zwischen zwei Energieniveaus 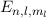 und
und 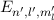 des Wasserstoffatoms unter Emission oder Absorption eines
Photons ist möglich, falls die Unterschiede der entsprechenden Quantenzahlen
des Wasserstoffatoms unter Emission oder Absorption eines
Photons ist möglich, falls die Unterschiede der entsprechenden Quantenzahlen
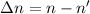 ,
, 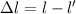 und
und 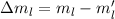 die folgenden Bedingungen
erfüllen
die folgenden Bedingungen
erfüllen

Da der Abstand 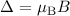 benachbarter Zeeman-Energieniveaus von den
Quantenzahlen
benachbarter Zeeman-Energieniveaus von den
Quantenzahlen 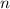 und
und 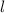 unabhängig ist, spalten sich die Frequenzen der erlaubten
Übergänge durch den Einfluss eines homogenen externen Magnetfelds in drei
Frequenzen auf (siehe Abb. 12.3). Diese drei Frequenzen werden Lorentzsches Triplett
genannt. Ist die Frequenz der Spektrallinie ohne Magnetfeld
unabhängig ist, spalten sich die Frequenzen der erlaubten
Übergänge durch den Einfluss eines homogenen externen Magnetfelds in drei
Frequenzen auf (siehe Abb. 12.3). Diese drei Frequenzen werden Lorentzsches Triplett
genannt. Ist die Frequenz der Spektrallinie ohne Magnetfeld 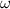 , dann sind die
Frequenzen im Lorentzschen Triplett gegeben durch
, dann sind die
Frequenzen im Lorentzschen Triplett gegeben durch
wie Lorentz schon auf rein klassischem Weg herausfand (siehe Abschnitt 12.1).
Wenn das Lorentzsche Triplett auftritt, dann spricht man vom normalen
Zeeman-Effekt. Die Gründe für diese Bezeichnung sind rein historisch. Es sei an dieser
Stelle bemerkt, dass der normale Zeeman-Effekt nur ein Spezialfall des sogenannten
anomalen Zeeman-Effekts ist, bei dem der Spin des Elektrons (siehe Kapitel 13)
mitberücksichtigt wird. Beim Wasserstoffatom ist deshalb in der Realität
die Aufspaltung komplizierter und nicht alleine durch den Bahndrehimpuls
erklärbar.
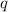 und der Masse
und der Masse 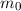 sich auf einer Kreisbahn mit
einem bestimmten Radius
sich auf einer Kreisbahn mit
einem bestimmten Radius 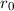 bewegen. Die Zentripetalbeschleunigung
bewegen. Die Zentripetalbeschleunigung 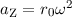 soll durch eine Zentripetalkraft
soll durch eine Zentripetalkraft 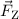 (unbekannten Ursprungs) erzeugt werden.
Befindet sich nun dieses Atom in einem homogenen Magnetfeld
(unbekannten Ursprungs) erzeugt werden.
Befindet sich nun dieses Atom in einem homogenen Magnetfeld 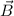 , welches
senkrecht zur Bahnrichtung der Ladung
, welches
senkrecht zur Bahnrichtung der Ladung 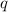 gerichtet ist, so wirkt auf diese die
Lorentz-Kraft
gerichtet ist, so wirkt auf diese die
Lorentz-Kraft 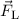 in radialer Richtung nach aussen oder nach innen abhängig
vom Umlaufsinn des Teilchens. Damit dieses auf seiner Bahn bleibt, muss
im ersten Fall die Winkelgeschwindigkeit
in radialer Richtung nach aussen oder nach innen abhängig
vom Umlaufsinn des Teilchens. Damit dieses auf seiner Bahn bleibt, muss
im ersten Fall die Winkelgeschwindigkeit 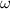 verkleinert, im zweiten Fall
vergrössert werden. Der Betrag der Lorentz-Kraft
verkleinert, im zweiten Fall
vergrössert werden. Der Betrag der Lorentz-Kraft 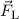 ist dabei gegeben
durch
ist dabei gegeben
durch

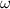 die Winkelgeschwindigkeit ohne Magnetfeld und
die Winkelgeschwindigkeit ohne Magnetfeld und 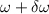 die
Winkelgeschwindigkeit mit Magnetfeld. Die durch das Magnetfeld bewirkte Änderung
die
Winkelgeschwindigkeit mit Magnetfeld. Die durch das Magnetfeld bewirkte Änderung
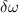 der Winkelgeschwindigkeit ergibt sich durch Gleichsetzen des Betrags
der Winkelgeschwindigkeit ergibt sich durch Gleichsetzen des Betrags 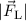 der
Lorentz-Kraft mit der Änderung der Zentripetalkraft
der
Lorentz-Kraft mit der Änderung der Zentripetalkraft 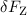 , wobei
, wobei 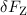 in erster
Näherung gegeben ist durch
in erster
Näherung gegeben ist durch


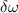 der
Winkelgeschwindigkeit das folgende Resultat erhalten
der
Winkelgeschwindigkeit das folgende Resultat erhalten

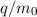 , das sich mit Hilfe der Interpretation
von Lorentz aus der experimentellen Abschätzung der Zeeman-Aufspaltung
, das sich mit Hilfe der Interpretation
von Lorentz aus der experimentellen Abschätzung der Zeeman-Aufspaltung
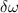 ergab und fand innerhalb der damals recht grossen Fehlerschranken
Übereinstimmung. Seit jener Zeit weiss man, dass das Elektron ein Bestandteil des
Atoms ist.
ergab und fand innerhalb der damals recht grossen Fehlerschranken
Übereinstimmung. Seit jener Zeit weiss man, dass das Elektron ein Bestandteil des
Atoms ist.
 hervor.
hervor. erzeugt, welcher ein
magnetisches Moment
erzeugt, welcher ein
magnetisches Moment  antiparallel zur Flächennormalen
antiparallel zur Flächennormalen 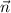 hervorruft
hervorruft

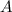 die von der Kreisbahn eingeschlossene Fläche bezeichnet. Der Strom
die von der Kreisbahn eingeschlossene Fläche bezeichnet. Der Strom 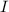 lässt sich durch die Elektronenladung
lässt sich durch die Elektronenladung 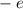 und die Umlauffrequenz
und die Umlauffrequenz  ausdrücken
und die Fläche
ausdrücken
und die Fläche 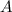 durch den Bahnradius
durch den Bahnradius  . Es ergibt sich
. Es ergibt sich

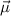 mit dem
Bahndrehimpuls
mit dem
Bahndrehimpuls 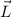 des Elektrons
des Elektrons


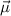 zu Bahndrehimpuls
zu Bahndrehimpuls 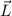 wird
wird
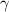 bezeichnet
bezeichnet

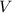 des Elektrons in einem homogenen
externen Magnetfeld
des Elektrons in einem homogenen
externen Magnetfeld 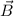 zu bestimmen. Sie ist gegeben durch
zu bestimmen. Sie ist gegeben durch

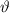 den Winkel zwischen magnetischem Moment
den Winkel zwischen magnetischem Moment 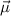 und Magnetfeld
und Magnetfeld 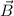 bezeichnet. Demzufolge erreicht die potentielle Energie
bezeichnet. Demzufolge erreicht die potentielle Energie 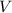 ihr Minimum für
ihr Minimum für
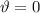 , d.h. wenn
, d.h. wenn 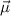 parallel zu
parallel zu 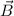 ausgerichtet ist und ihr Maximum
für
ausgerichtet ist und ihr Maximum
für 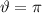 , d.h. wenn
, d.h. wenn 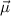 antiparallel zu
antiparallel zu 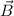 ausgerichtet ist. Mit (
ausgerichtet ist. Mit (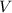 des Elektrons mit Bahndrehimpuls
des Elektrons mit Bahndrehimpuls
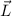

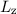 des
Bahndrehimpulses
des
Bahndrehimpulses 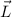 gegeben durch
gegeben durch

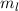 nur die diskreten Werte
nur die diskreten Werte 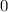 ,
,  ,
, 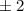 , ...
annehmen kann. Somit ergibt sich für die potentielle Energie
, ...
annehmen kann. Somit ergibt sich für die potentielle Energie 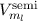 des
magnetischen Moments des Elektrons im Wasserstoffatom
des
magnetischen Moments des Elektrons im Wasserstoffatom

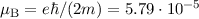 eV/T das
eV/T das 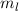 eingeführt haben und der obere Index semi andeuten soll,
dass unsere Herleitung semiklassisch erfolgte.
eingeführt haben und der obere Index semi andeuten soll,
dass unsere Herleitung semiklassisch erfolgte. 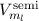 wird Zeeman-Energie
genannt. Damit ergibt sich für die Energiewerte
wird Zeeman-Energie
genannt. Damit ergibt sich für die Energiewerte 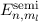 des Wasserstoffatoms
(siehe Abschnitt
des Wasserstoffatoms
(siehe Abschnitt  die folgende
Korrektur
die folgende
Korrektur
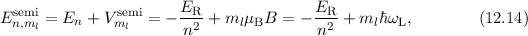
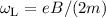 die
die 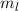 eingeführt haben. Das bedeutet, dass durch ein
homogenes externes Magnetfeld
eingeführt haben. Das bedeutet, dass durch ein
homogenes externes Magnetfeld 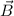 die durch die magnetische Quantenzahl
die durch die magnetische Quantenzahl 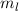 bewirkte
bewirkte 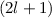 -fache Entartung der Energiewerte
-fache Entartung der Energiewerte 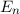 aufgehoben wird (siehe
Abb.
aufgehoben wird (siehe
Abb. 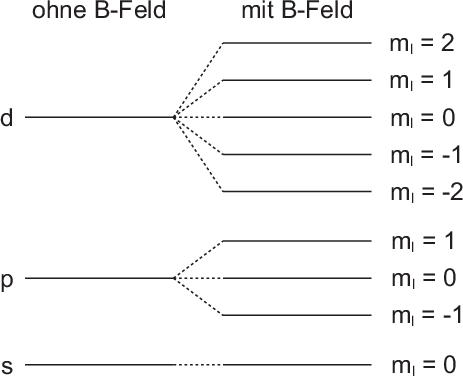
 -,
-, 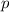 -,
-, 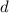 -Energieniveaus des
Wasserstoffatoms im homogenen externen Magnetfeld (Hinweis: Abbildung ist
nicht massstabsgerecht).
-Energieniveaus des
Wasserstoffatoms im homogenen externen Magnetfeld (Hinweis: Abbildung ist
nicht massstabsgerecht). -Niveaus (
-Niveaus (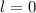 ,
, 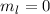 ) werden durch das Magnetfeld nicht beeinflusst.
Die
) werden durch das Magnetfeld nicht beeinflusst.
Die 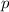 -Niveaus (
-Niveaus (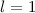 ,
, 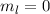 ,
,  ) werden in drei und die
) werden in drei und die 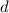 -Niveaus
(
-Niveaus
(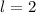 ,
, 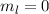 ,
,  ,
, 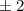 ) in fünf Niveaus mit Abstand
) in fünf Niveaus mit Abstand 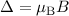 aufgespaltet.
aufgespaltet.
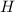 für ein Teilchen der Ladung
für ein Teilchen der Ladung
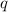 und der Masse
und der Masse 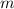 im Magnetfeld
im Magnetfeld 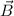 (für eine Motivation verweisen wir auf
Anhang
(für eine Motivation verweisen wir auf
Anhang 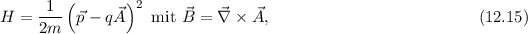
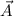 das sogenannte
das sogenannte 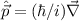 erhalten wir
für den entsprechenden Hamilton-Operator
erhalten wir
für den entsprechenden Hamilton-Operator 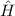 den folgenden Ausdruck
den folgenden Ausdruck
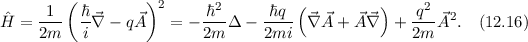
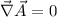 und erhalten
und erhalten

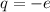 ) im homogenen
Magnetfeld
) im homogenen
Magnetfeld 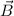 . Ohne Beschränkung der Allgemeinheit wählen wir
. Ohne Beschränkung der Allgemeinheit wählen wir 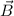 entlang der
z-Achse, d.h.
entlang der
z-Achse, d.h. 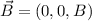 . Das entsprechende Vektorpotential
. Das entsprechende Vektorpotential 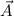 können wir
schreiben als
können wir
schreiben als
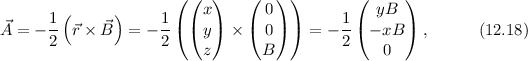
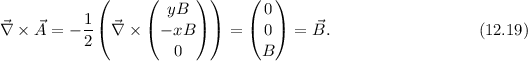
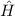 eines
Elektrons im homogenen Magnetfeld
eines
Elektrons im homogenen Magnetfeld
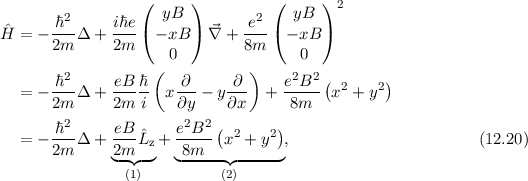
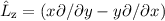 .
.
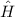 von Elektronen in Atomen. Wir benützen dazu, dass
von Elektronen in Atomen. Wir benützen dazu, dass 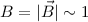 T,
T,
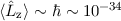 Js,
Js, 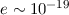 C,
C, 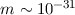 kg,
kg, 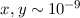 m und
erhalten
m und
erhalten
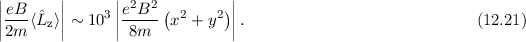
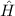 für das Wasserstoffatom im homogenen externen
Magnetfeld
für das Wasserstoffatom im homogenen externen
Magnetfeld
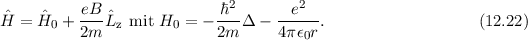
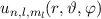 sowohl Eigenfunktionen
des Hamilton-Operators
sowohl Eigenfunktionen
des Hamilton-Operators 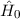 mit den Eigenwerten
mit den Eigenwerten 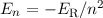 als auch des
Operators
als auch des
Operators 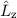 mit den Eigenwerten
mit den Eigenwerten 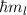 . Deshalb gilt
. Deshalb gilt
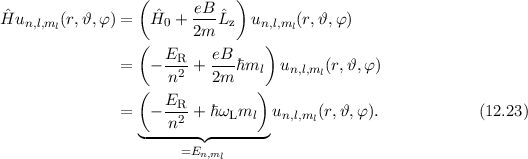
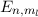 des Wasserstoffatoms im homogenen externen
Magnetfeld gegeben durch
des Wasserstoffatoms im homogenen externen
Magnetfeld gegeben durch

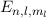 und
und 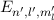 des Wasserstoffatoms unter Emission oder Absorption eines
Photons ist möglich, falls die Unterschiede der entsprechenden Quantenzahlen
des Wasserstoffatoms unter Emission oder Absorption eines
Photons ist möglich, falls die Unterschiede der entsprechenden Quantenzahlen
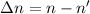 ,
, 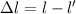 und
und 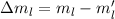 die folgenden Bedingungen
erfüllen
die folgenden Bedingungen
erfüllen

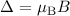 benachbarter Zeeman-Energieniveaus von den
Quantenzahlen
benachbarter Zeeman-Energieniveaus von den
Quantenzahlen 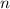 und
und 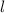 unabhängig ist, spalten sich die Frequenzen der erlaubten
Übergänge durch den Einfluss eines homogenen externen Magnetfelds in drei
Frequenzen auf (siehe Abb.
unabhängig ist, spalten sich die Frequenzen der erlaubten
Übergänge durch den Einfluss eines homogenen externen Magnetfelds in drei
Frequenzen auf (siehe Abb. 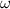 , dann sind die
Frequenzen im Lorentzschen Triplett gegeben durch
, dann sind die
Frequenzen im Lorentzschen Triplett gegeben durch

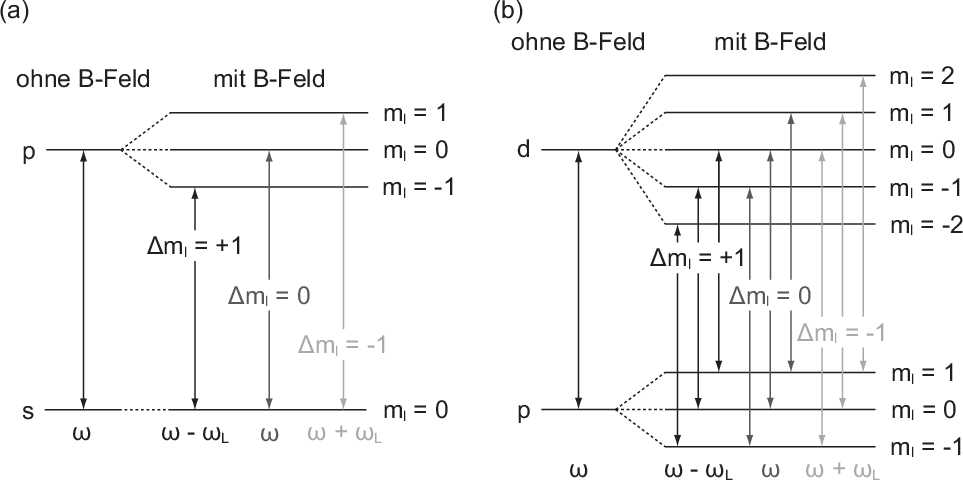
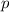 - und
- und  -Niveaus und
(b)
-Niveaus und
(b)  - und
- und  -Niveaus (Hinweis: Abbildung ist nicht massstabsgerecht).
-Niveaus (Hinweis: Abbildung ist nicht massstabsgerecht).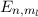 des
Wasserstoffatoms im homogenen externen Magnetfeld
des
Wasserstoffatoms im homogenen externen Magnetfeld

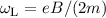 die Larmor-Frequenz bezeichnet. Das bedeutet, dass
durch ein homogenes externes Magnetfeld
die Larmor-Frequenz bezeichnet. Das bedeutet, dass
durch ein homogenes externes Magnetfeld 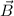 die durch die magnetische
Quantenzahl
die durch die magnetische
Quantenzahl 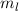 bewirkte
bewirkte 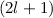 -fache Entartung der Energiewerte
-fache Entartung der Energiewerte 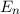 aufgehoben wird.
aufgehoben wird.
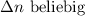 ,
, 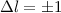 ,
, 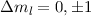 . Der
Abstand
. Der
Abstand 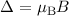 benachbarter Zeeman-Energieniveaus ist von den
Quantenzahlen
benachbarter Zeeman-Energieniveaus ist von den
Quantenzahlen 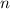 und
und 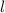 unabhängig, weshalb sich die Frequenzen der
erlaubten Übergänge durch den Einfluss eines homogenen externen Magnetfelds
in drei Frequenzen aufspalten. Diese drei Frequenzen werden Lorentzsches
Triplett genannt.
unabhängig, weshalb sich die Frequenzen der
erlaubten Übergänge durch den Einfluss eines homogenen externen Magnetfelds
in drei Frequenzen aufspalten. Diese drei Frequenzen werden Lorentzsches
Triplett genannt.