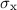 ,
, 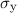 und
und 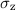 kennengelernt.
Wir geben an dieser Stelle eine Herleitung dieser Matrizen an.
kennengelernt.
Wir geben an dieser Stelle eine Herleitung dieser Matrizen an.
In Abschnitt 13.3 haben wir die Pauli-Matrizen 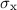 ,
, 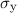 und
und 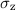 kennengelernt.
Wir geben an dieser Stelle eine Herleitung dieser Matrizen an.
kennengelernt.
Wir geben an dieser Stelle eine Herleitung dieser Matrizen an.
Die Pauli-Matrix 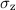 ergibt sich aus der Anwendung von
ergibt sich aus der Anwendung von 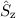 auf die beiden
Basiszustände
auf die beiden
Basiszustände 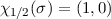 und
und 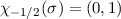 . Mit (13.12) ergibt
sich
. Mit (13.12) ergibt
sich
und somit in Übereinstimmung mit (13.25) für 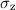 das folgende Resultat
das folgende Resultat
Für die Bestimmung der Pauli-Matrizen 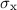 und
und 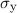 leiten wir die Eigenschaften
und die Matrizendarstellung der in Abschnitt 13.3.1 eingeführten Leiteroperatoren
leiten wir die Eigenschaften
und die Matrizendarstellung der in Abschnitt 13.3.1 eingeführten Leiteroperatoren
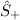 und
und 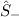 unabhängig von der Matrizendarstellung für die Spinmatrizen
unabhängig von der Matrizendarstellung für die Spinmatrizen 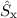 und
und
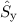 her.
her.
Die Leiteroperatoren 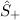 und
und  sind nach (13.28) und (13.29) gegeben
durch
sind nach (13.28) und (13.29) gegeben
durch
Wir geben als erstes ein paar Eigenschaften dieser beiden Operatoren an:
mit (K.5) und (K.6) ergibt sich
und in Analogie zu (11.15) gilt
Wir wenden nun den Operator 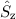 auf die Zustände
auf die Zustände 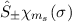 an und untersuchen
damit den Einfluss der Leiteroperatoren
an und untersuchen
damit den Einfluss der Leiteroperatoren 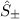 auf die magnetische Spinquantenzahl
auf die magnetische Spinquantenzahl
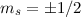 . Wir erhalten
. Wir erhalten
Somit erhöht (erniedrigt) der Operator 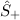 (
(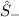 ) die Quantenzahl
) die Quantenzahl 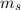 um 1. Auf
analoge Weise untersuchen wir den Einfluss der Leiteroperatoren
um 1. Auf
analoge Weise untersuchen wir den Einfluss der Leiteroperatoren 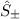 auf die
Spinquantenzahl
auf die
Spinquantenzahl 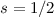 . Es gilt
. Es gilt
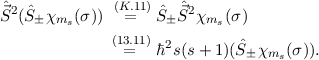
Folglich bleibt die Spinquantenzahl 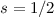 unverändert bei der Anwendung der
Leiteroperatoren
unverändert bei der Anwendung der
Leiteroperatoren 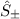 .
.
Als nächstes betrachten wir die Norm der Zustände 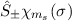 und erhalten
mit (K.5), (K.6), (13.10) und (13.11)
und erhalten
mit (K.5), (K.6), (13.10) und (13.11)
wobei wir im letzten Schritt verwendet haben, dass die Spinwellenfunktionen
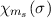 auf 1 normiert sind. Zusammen mit dem erhaltenen Verhalten der
Quantenzahlen
auf 1 normiert sind. Zusammen mit dem erhaltenen Verhalten der
Quantenzahlen  und
und 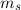 unter der Anwendung der Leiteroperatoren
unter der Anwendung der Leiteroperatoren 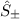 erhalten
wir damit die folgende Gleichung
erhalten
wir damit die folgende Gleichung
Mit 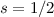 und
und 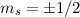 ergibt sich daraus für die Anwendung der
Leiteroperatoren
ergibt sich daraus für die Anwendung der
Leiteroperatoren  auf die beiden Basiszustände
auf die beiden Basiszustände 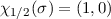 und
und
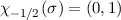
Folglich lassen sich die beiden Leiteroperatoren 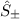 durch die folgenden Matrizen
darstellen
durch die folgenden Matrizen
darstellen
Damit folgt für die beiden Operatoren 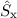 und
und 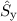
und somit in Übereinstimmung mit (13.25) für 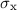 und
und 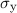 das folgende
Resultat
das folgende
Resultat