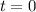 in einem
Zustand
in einem
Zustand 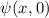 befindet, welcher durch eine (normierte) Dreiecksfunktion
beschrieben werden kann (siehe Abb. D.1)
befindet, welcher durch eine (normierte) Dreiecksfunktion
beschrieben werden kann (siehe Abb. D.1)
Wir betrachten ein Teilchen im Potentialtopf, welches sich zur Zeit 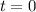 in einem
Zustand
in einem
Zustand 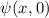 befindet, welcher durch eine (normierte) Dreiecksfunktion
beschrieben werden kann (siehe Abb. D.1)
befindet, welcher durch eine (normierte) Dreiecksfunktion
beschrieben werden kann (siehe Abb. D.1)
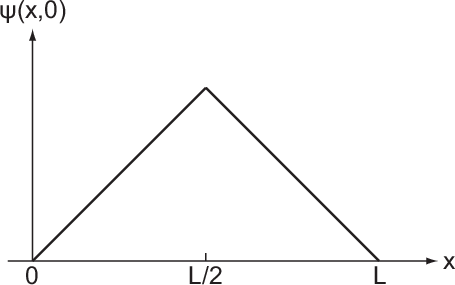
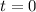 durch
eine Dreiecksfunktion beschrieben.
durch
eine Dreiecksfunktion beschrieben.Das Ziel ist es nun diesen Zustand entsprechend dem Satz 9.5 nach den Eigenfunktionen des Hamilton-Operators des Teilchens im Potentialtopf zu entwickeln. Diese sind nach (9.128) gegeben durch
wobei
Nach Satz 9.5 gilt
Wir berechnen nun für unser Beispiel die Entwicklungskoeffizienten 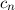 . Es ergibt
sich mit (D.1) und (D.3)
. Es ergibt
sich mit (D.1) und (D.3)
Einsetzen in (D.4) ergibt für die Wellenfunktion 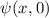 zur Zeit
zur Zeit 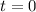 die
folgende Entwicklung
die
folgende Entwicklung
Den Zeitverlauf der Wellenfunktion 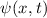 ergibt sich nun aus der bekannten
Zeitabhängigkeit der stationären Zustände
ergibt sich nun aus der bekannten
Zeitabhängigkeit der stationären Zustände 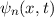 (D.2). Wir erhalten damit die
folgende Lösung
(D.2). Wir erhalten damit die
folgende Lösung