 und den Impuls
und den Impuls 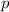 , beschränken. Dabei soll jedoch darauf hingewiesen
werden, dass die Postulate und hergeleiteten Sätze auch für drei Dimensionen
gelten.
, beschränken. Dabei soll jedoch darauf hingewiesen
werden, dass die Postulate und hergeleiteten Sätze auch für drei Dimensionen
gelten.
In den vorangegangenen Kapiteln haben wir uns mit physikalischen Situationen und experimentellen Ergebnissen auseinandergesetzt, bei denen die klassische Physik nicht mehr ausreicht, um die beobachteten Phänomene befriedigend zu erklären. Diese Problematik motivierte die Einführung der Quantenmechanik. In Kapitel 8 haben wir z.B. erkannt, dass das Bohrsche Atommodell grundlegende Eigenschaften der Spektren von Atomen mit einem Elektron mit Hilfe semiklassischer Annahmen, die auf der Beschreibung der Eigenschaften von Teilchen durch Materiewellen beruhen, erklären kann. Um ein detailliertes physikalisches Verständnis von Atomen in elektromagnetischen Feldern oder Atomen mit mehreren Elektronen zu erlangen, erkannte man am Anfang des letzten Jahrhunderts schnell, dass eine vollständig neue Theorie, die heute als Quantenmechanik bekannt ist, benötigt werden würde.
Historisch gesehen wurden die Grundlagen der Quantenmechanik in den Jahren 1925 und 1926 mit Hilfe wichtiger Beiträge bekannter Physiker wie Erwin Schrödinger1, Werner Heisenberg, Max Born, Paul Dirac und anderer entwickelt. Das grundlegende Ziel war eine Theorie zu entwickeln, die die Welleneigenschaften von Teilchen korrekt beschreibt. Schon bis in die 1930er Jahre, kurz nach ihrer Entwicklung, konnten eine grosse Anzahl von Beobachtungen und Experimenten in der Physik und auch der Chemie durch diese neue Theorie erklärt werden.
In diesem Kapitel beschäftigen wir uns nun mit den wichtigen Aspekten des Formalismus der Quantenmechanik. Die Theorie basiert auf einigen wenigen grundlegenden Postulaten, mit deren Hilfe alle Beobachtungen von quantenmechanischen Phänomenen in der Natur korrekt beschrieben werden können. Bis heute hat noch kein Experiment den Vorhersagen der Quantenmechanik widersprochen.
Hier führen wir in die Grundlagen der Quantenmechanik basierend auf der
Wellenmechanik von de Broglie ein (siehe Kapitel 6). Wir werden uns dabei zunächst
auf die quantenmechanischen Eigenschaften der Dynamik einzelner Teilchen
(Massepunkte) in einer Dimension, beschrieben durch die Ortskoordinate
 und den Impuls
und den Impuls 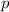 , beschränken. Dabei soll jedoch darauf hingewiesen
werden, dass die Postulate und hergeleiteten Sätze auch für drei Dimensionen
gelten.
, beschränken. Dabei soll jedoch darauf hingewiesen
werden, dass die Postulate und hergeleiteten Sätze auch für drei Dimensionen
gelten.
Zur Formulierung des ersten Postulats der Quantenmechanik benötigen wir die folgende Definition:
Definition 9.1 Eine Funktion 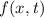 heisst quadratisch integrabel, falls
gilt
heisst quadratisch integrabel, falls
gilt
wobei 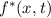 die komplex konjugierte Funktion von
die komplex konjugierte Funktion von 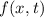 bezeichnet. Der Raum
aller quadratisch integrablen Funktionen wird mit
bezeichnet. Der Raum
aller quadratisch integrablen Funktionen wird mit 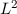 bezeichnet.
bezeichnet.
Postulat 1 Zu
einem Teilchen (Massepunkt) gehört eine eindeutige, quadratisch integrable, im
Allgemeinen komplexe Wellenfunktion 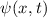 . Sie beschreibt den Zustand des
Teilchens. Dabei gibt
. Sie beschreibt den Zustand des
Teilchens. Dabei gibt 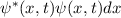 die Wahrscheinlichkeit an das Teilchen
zur Zeit
die Wahrscheinlichkeit an das Teilchen
zur Zeit 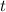 zwischen
zwischen  und
und 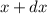 anzutreffen. Die Grösse
anzutreffen. Die Grösse 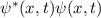 wird daher als Wahrscheinlichkeitsdichte bezeichnet.
wird daher als Wahrscheinlichkeitsdichte bezeichnet.
Wir diskutieren zunächst einige wichtige Aspekte dieses Postulats. Da die
Wellenfunktion quadratisch integrabel ist, kann sie normiert werden. Dazu
ziehen wir die Bedingung heran, dass die Wahrscheinlichkeit, das Teilchen zur
Zeit 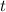 irgendwo auf der x-Achse anzutreffen 100% ist. Daher lautet die
Normierungsbedingung
irgendwo auf der x-Achse anzutreffen 100% ist. Daher lautet die
Normierungsbedingung
Weiter gilt nach dem Postulat 1, dass der Zustand des Teilchens durch die
Wellenfunktion 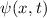 bestimmt ist. Somit sind alle Informationen über die
quantenmechanischen Eigenschaften eines Teilchens in
bestimmt ist. Somit sind alle Informationen über die
quantenmechanischen Eigenschaften eines Teilchens in 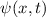 enthalten.
Experimentell erfassbare Grössen werden in der Quantenmechanik durch
Erwartungswerte charakterisiert. Nach der Wahrscheinlichkeitsrechnung gilt folgende
Definition.
enthalten.
Experimentell erfassbare Grössen werden in der Quantenmechanik durch
Erwartungswerte charakterisiert. Nach der Wahrscheinlichkeitsrechnung gilt folgende
Definition.
Definition 9.2 Der Erwartungswert einer Funktion 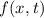 , die eine gegebene
physikalische Messgrösse beschreibt, ist für einen bestimmten Zeitpunkt
, die eine gegebene
physikalische Messgrösse beschreibt, ist für einen bestimmten Zeitpunkt 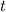 gegeben
durch
gegeben
durch
Dabei ist zu beachten, dass die instruktive Umformung in der zweiten Zeile nur dann
gilt, wenn die Funktion 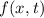 reelle oder komplexe Werte annimmt. Handelt es sich
bei der Funktion um einen sogenannten Operator, so ist (9.3) in der gegebenen Form
explizit zu verwenden, wie wir in Abschnitt 9.3 einsehen werden. Beispiele für
Funktionen
reelle oder komplexe Werte annimmt. Handelt es sich
bei der Funktion um einen sogenannten Operator, so ist (9.3) in der gegebenen Form
explizit zu verwenden, wie wir in Abschnitt 9.3 einsehen werden. Beispiele für
Funktionen 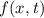 sind die Ortskoordinate
sind die Ortskoordinate 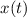 des Teilchens oder seine
potentielle Energie
des Teilchens oder seine
potentielle Energie 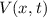 .
.
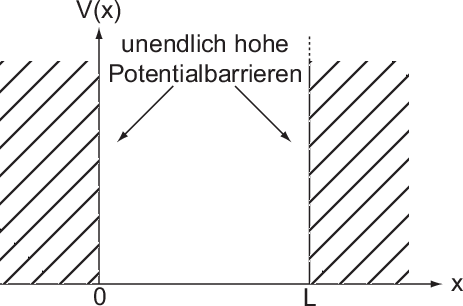
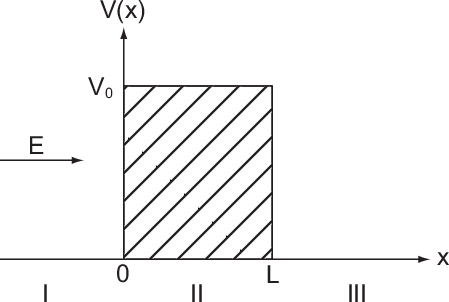
Zur Veranschaulichung des ersten Postulats betrachten wir ein Teilchen in einem eindimensionalen Potentialtopf (siehe Abb. 9.1).
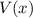 in Abhängigkeit von
in Abhängigkeit von  für ein Teilchen im
Potentialtopf. Unendlich hohe Potentialbarrieren beschränken das Teilchen auf
den Bereich
für ein Teilchen im
Potentialtopf. Unendlich hohe Potentialbarrieren beschränken das Teilchen auf
den Bereich 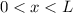 .
.D.h. die Bewegung des Teilchens entlang der x-Richtung ist durch harte Wände an
den Positionen 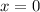 und
und 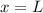 eingeschränkt. Damit sind die Gebiete
eingeschränkt. Damit sind die Gebiete 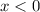 und
und 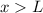 für das Teilchen nicht erreichbar. Diese Tatsache wird durch das folgende
Potential
für das Teilchen nicht erreichbar. Diese Tatsache wird durch das folgende
Potential 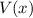 beschrieben
beschrieben
Wir betrachten das Teilchen nun als Materiewelle. Im Bereich 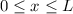 kann sich
das Teilchen frei bewegen. Daher setzen wir für die Wellenfunktion
kann sich
das Teilchen frei bewegen. Daher setzen wir für die Wellenfunktion 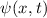 , die den
Zustand des Teilchens in diesem Bereich beschreibt, die Wellenfunktion für ein freies
Teilchen an. Nach (6.17) gilt
, die den
Zustand des Teilchens in diesem Bereich beschreibt, die Wellenfunktion für ein freies
Teilchen an. Nach (6.17) gilt
Klassisch gesehen besteht für ein freies Teilchen zwischen der Energie 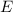 und dem
Impuls
und dem
Impuls 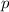 die folgende Beziehung
die folgende Beziehung
D.h. bei konstanter Energie 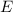 kann der Impuls
kann der Impuls 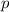 in einer Dimension zwei
mögliche Werte annehmen, die einer Bewegung des Teilchens entlang der positiven
oder negative Koordinatenachse entspricht. Wir erweitern daher unseren Ansatz zu
einer Superposition von einer nach rechts und einer nach links laufenden
Materiewelle
in einer Dimension zwei
mögliche Werte annehmen, die einer Bewegung des Teilchens entlang der positiven
oder negative Koordinatenachse entspricht. Wir erweitern daher unseren Ansatz zu
einer Superposition von einer nach rechts und einer nach links laufenden
Materiewelle
Nun berücksichtigen wir, dass die freie Bewegung des Teilchens auf den Bereich
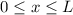 beschränkt ist. D.h. die betrachtete Wellenfunktion muss folgenden
Randbedingungen genügen
beschränkt ist. D.h. die betrachtete Wellenfunktion muss folgenden
Randbedingungen genügen
Aus 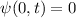 folgt
folgt 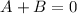 . Damit erhalten wir
. Damit erhalten wir
Aus 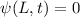 folgt
folgt 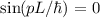 und damit
und damit 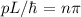 mit
mit 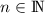 . Woraus
wir die Bedingung erhalten, dass der Impuls
. Woraus
wir die Bedingung erhalten, dass der Impuls 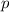 und damit die Energie
und damit die Energie 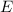 des
Teilchens im Potentialtopf nur diskrete Werte
des
Teilchens im Potentialtopf nur diskrete Werte 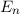 annehmen kann
annehmen kann
Hier erkennen wir, dass die Beschreibung eines Teilchens in einem Potentialtopf als Materiewelle auf natürliche Art und Weise zu einer diskreten Abfolge von möglichen Energiewerten des Teilchens, also zu einer Quantisierung, führt.
Die Wellenfunktion 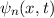 zur Energie
zur Energie 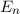 nimmt damit die folgende Form
an
nimmt damit die folgende Form
an
Zur Bestimmung der Konstanten 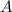 ziehen wir nun die Normierungsbedingung (9.2)
heran. Wir erhalten
ziehen wir nun die Normierungsbedingung (9.2)
heran. Wir erhalten
Daraus ergibt sich 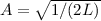 und somit für die Wellenfunktion
und somit für die Wellenfunktion 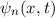 zur
Energie
zur
Energie 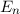 für das Teilchen im Potentialtopf das folgende Resultat (siehe
Abb. 9.2)
für das Teilchen im Potentialtopf das folgende Resultat (siehe
Abb. 9.2)
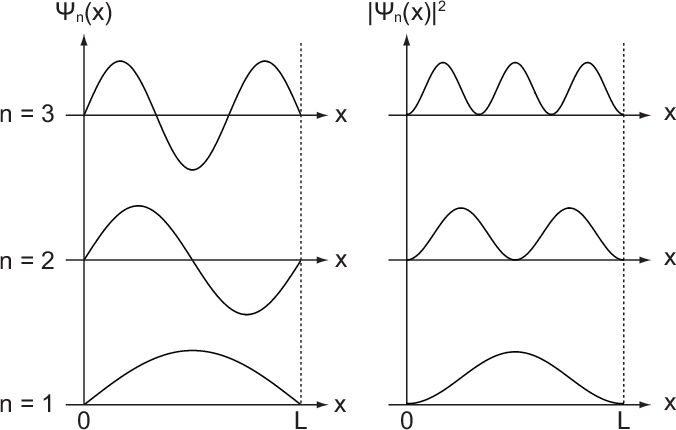
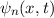 und die entsprechenden Wahrscheinlichkeitsdichten
und die entsprechenden Wahrscheinlichkeitsdichten
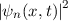 für die Zustände
für die Zustände 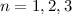 für ein Teilchen im Potentialtopf.
für ein Teilchen im Potentialtopf.Ein Potentialtopf, wie wir ihn hier besprochen haben, ist ein gutes Modell für die Energieniveaus von Elektronen in sogenannten Quantenpunkten (quantum dots). Die Elektronen in Quantenpunkten sind in ihrer Beweglichkeit in allen drei Raumrichtungen eingeschränkt. Realisiert werden Quantenpunkte in sogenannten Nanostrukturen, welche grösstenteils aus verschiedenen Halbleitermaterialien aufgebaut sind.
Bisher haben wir die Wellenfunktion als eine Funktion der Ortsvariablen  betrachtet. Wir haben also die sogenannte Ortsraumdarstellung gewählt. Anstelle der
Ortskoordinate
betrachtet. Wir haben also die sogenannte Ortsraumdarstellung gewählt. Anstelle der
Ortskoordinate  kann jedoch auch der entsprechende Impuls
kann jedoch auch der entsprechende Impuls 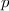 als Variable
eingeführt werden. Man postuliert dann eine weitere, ebenfalls eindeutige,
quadratisch integrable, im Allgemeinen komplexe Wellenfunktion
als Variable
eingeführt werden. Man postuliert dann eine weitere, ebenfalls eindeutige,
quadratisch integrable, im Allgemeinen komplexe Wellenfunktion 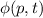 , die den
Zustand des Teilchens im folgenden Sinn beschreibt:
, die den
Zustand des Teilchens im folgenden Sinn beschreibt: 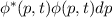 ist die
Wahrscheinlichkeit, dass das Teilchen zur Zeit
ist die
Wahrscheinlichkeit, dass das Teilchen zur Zeit 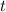 einen Impuls zwischen
einen Impuls zwischen 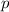 und
und
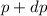 besitzt.
besitzt.
Auch für diese Wellenfunktion gilt eine Normierungsbedingung
Wir können auch hier für eine Funktion 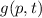 , die sich aufs Teilchen bezieht, den
entsprechenden Erwartungswert definieren.
, die sich aufs Teilchen bezieht, den
entsprechenden Erwartungswert definieren.
Definition 9.3 Der Erwartungswert einer Funktion 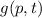 ist für einen
bestimmten Zeitpunkt
ist für einen
bestimmten Zeitpunkt 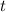 gegeben durch
gegeben durch
Hier gelten die selben Einschränkungen wie wir sie bereits für die Wellenfunktionen
im Ortsraum diskutiert haben. Beispiele für die Funktion 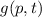 sind der Impuls
sind der Impuls
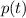 des Teilchens oder seine kinetische Energie
des Teilchens oder seine kinetische Energie 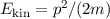 .
.
Nun untersuchen wir, welcher Zusammenhang zwischen der Wellenfunktion 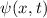 im Ortsraum und der Wellenfunktion
im Ortsraum und der Wellenfunktion 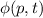 im Impulsraum besteht. Wir
betrachten dazu ein Teilchen mit konstanter Gesamtenergie
im Impulsraum besteht. Wir
betrachten dazu ein Teilchen mit konstanter Gesamtenergie 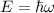 , z.B. ein
Teilchen, das sich mit konstanter kinetischer Energie in einem konstanten Potential
, z.B. ein
Teilchen, das sich mit konstanter kinetischer Energie in einem konstanten Potential
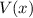 bewegt. Der Zustand wird durch ein entsprechendes Wellenpaket
bewegt. Der Zustand wird durch ein entsprechendes Wellenpaket 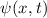 beschrieben (siehe Abschnitt 6.4)
beschrieben (siehe Abschnitt 6.4)
Dabei ist 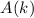 durch die entsprechende Fourier-Transformierte gegeben
durch die entsprechende Fourier-Transformierte gegeben
Mit der de Broglie-Beziehung 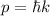 folgt damit, dass auch die Wellenfunktionen
im Orts- bzw. Impulsraum
folgt damit, dass auch die Wellenfunktionen
im Orts- bzw. Impulsraum 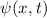 und
und 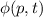 durch eine Fourier-Transformation
miteinander verbunden sind. Es gilt
durch eine Fourier-Transformation
miteinander verbunden sind. Es gilt
In der klassischen Mechanik sind die Eigenschaften eines Teilchens, wie zum Beispiel
sein Ort  und sein Impuls
und sein Impuls 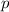 , gleichzeitig beliebig genau bestimmt. Diese
Eigenschaften lassen sich im Prinzip mit beliebiger, nur durch die Messapparatur
begrenzter, Genauigkeit in einer Messung bestimmen.
, gleichzeitig beliebig genau bestimmt. Diese
Eigenschaften lassen sich im Prinzip mit beliebiger, nur durch die Messapparatur
begrenzter, Genauigkeit in einer Messung bestimmen.
Im Gegensatz dazu ist eine charakteristische Eigenschaft der Quantenmechanik, dass
der Ort  und der Impuls
und der Impuls 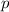 eines Teilchens nicht gleichzeitig beliebig genau
bestimmt sind. Versucht man zum Beispiel
eines Teilchens nicht gleichzeitig beliebig genau
bestimmt sind. Versucht man zum Beispiel  und
und 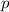 gleichzeitig zu messen, so gilt,
dass das Produkt der Standardabweichungen der Messresultate für Ort und Impuls
immer grösser ist als eine Konstante, die durch die Quantenmechanik bestimmt ist.
Diese Eigenschaft der Quantenmechanik wird als Heisenbergsche Unschärferelation
bezeichnet.
gleichzeitig zu messen, so gilt,
dass das Produkt der Standardabweichungen der Messresultate für Ort und Impuls
immer grösser ist als eine Konstante, die durch die Quantenmechanik bestimmt ist.
Diese Eigenschaft der Quantenmechanik wird als Heisenbergsche Unschärferelation
bezeichnet.
Diese Unschärferelation gilt nicht nur für Ort und Impuls eines Teilchens sondern auch für andere Grössen, wie z.B. Energie und Zeit oder die Komponenten des Bahndrehimpulses in drei Dimensionen, wie wir später kennen lernen werden.
Bevor wir uns der Einbettung der Unschärferelation in die Wellenmechanik zuwenden, betrachten wir als Illustration die Beugung einer Materiewelle am Spalt.
Im betrachteten Versuch (siehe Abb. 9.3) bewegt sich ein Teilchenstrom von links auf
einen Spalt der Breite 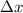 zu.
zu.
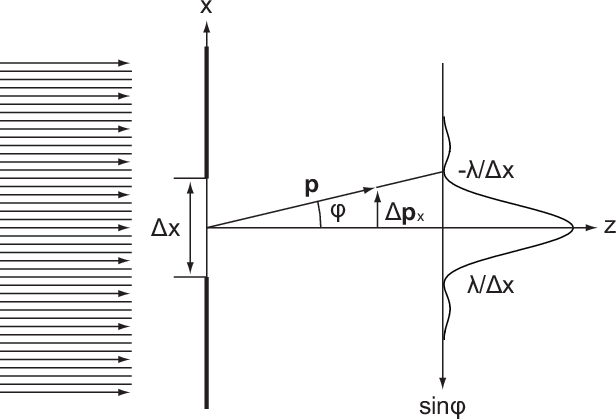
Der Spalt sei bei 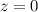 positioniert. Vor dem Spalt, d.h. für
positioniert. Vor dem Spalt, d.h. für 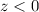 , kennt man die
x-Koordinate des Teilchens nicht, dafür ist die Impulskomponente
, kennt man die
x-Koordinate des Teilchens nicht, dafür ist die Impulskomponente 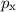 genau
bekannt. Trifft nun dieser Teilchenstrahl auf den Spalt, so erfolgt eine Selektion der
Teilchen. Die x-Koordinate ist dann bis auf die Unschärfe
genau
bekannt. Trifft nun dieser Teilchenstrahl auf den Spalt, so erfolgt eine Selektion der
Teilchen. Die x-Koordinate ist dann bis auf die Unschärfe 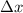 bekannt. Jedoch gibt
es durch die Beugung am Spalt Teilchen, die unter einem nicht verschwindenden
Winkel
bekannt. Jedoch gibt
es durch die Beugung am Spalt Teilchen, die unter einem nicht verschwindenden
Winkel 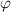 auslaufen. Die Wahrscheinlichkeitsverteilung ergibt sich aus der Beugung
der Materiewelle (de Broglie-Welle). Die meisten Teilchen treffen in den
Winkelbereich
auslaufen. Die Wahrscheinlichkeitsverteilung ergibt sich aus der Beugung
der Materiewelle (de Broglie-Welle). Die meisten Teilchen treffen in den
Winkelbereich
Damit kann die in Abb. 9.3 eingezeichnete Grösse 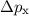 als Unschärfe der
Impulskomponente
als Unschärfe der
Impulskomponente 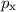 aufgefasst werden. Es gilt dabei der folgende Zusammenhang
aufgefasst werden. Es gilt dabei der folgende Zusammenhang
Mit der de Broglie-Beziehung 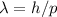 erhalten wir
erhalten wir
Berücksichtigt man die Tatsache, dass einige Teilchen auch in die Nebenmaxima fallen, so wird aus der Gleichung eine Ungleichung
Diese Ungleichung besagt, dass die Ortskoordinate  und die Impulskomponente
und die Impulskomponente
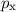 gleichzeitig nicht beliebig genau bestimmbar sind.
gleichzeitig nicht beliebig genau bestimmbar sind.
In diesem Abschnitt haben wir den Begriff der Unschärfe anhand eines Beispiels eingeführt. Nun wenden wir uns der formalen Berechnung der Unschärferelation eines Teilchens im Rahmen der Wellenmechanik zu.
Definition 9.4 Entsprechend den Gesetzen der Wahrscheinlichkeitsrechnung ist die
Unschärfe 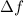 einer Grösse
einer Grösse 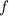 bestimmt durch die Standardabweichung, die
durch die Wurzel des Erwartungswerts der Quadrate der Abweichungen vom
Erwartungswert gegeben ist
bestimmt durch die Standardabweichung, die
durch die Wurzel des Erwartungswerts der Quadrate der Abweichungen vom
Erwartungswert gegeben ist
Wir wenden diese Definition 9.4 auf ein Teilchen an, dessen Zustand durch eine reelle
Wellenfunktion 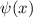 beschrieben ist (für genaue Ausführungen der folgenden
Berechnungen verweisen wir auf Anhang A).
beschrieben ist (für genaue Ausführungen der folgenden
Berechnungen verweisen wir auf Anhang A). 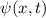 ist so beschaffen, dass die
Wahrscheinlichkeitsdichte
ist so beschaffen, dass die
Wahrscheinlichkeitsdichte 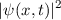 des Teilchens einer Gauss-Verteilung
entspricht
des Teilchens einer Gauss-Verteilung
entspricht
und somit ein Wellenpaket der charakteristischen Breite  formt. Diese Funktion ist
normiert, d.h. es gilt
formt. Diese Funktion ist
normiert, d.h. es gilt
Für den Erwartungswert  der Ortskoordinate erhalten wir
der Ortskoordinate erhalten wir
d.h. 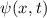 beschreibt ein Teilchen, das sich im Mittel bei
beschreibt ein Teilchen, das sich im Mittel bei 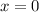 aufhält. Damit
ergibt sich für die Unschärfe
aufhält. Damit
ergibt sich für die Unschärfe 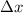 der Ortskoordinate
der Ortskoordinate
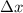 entspricht also gerade der Breite der Gauss-Verteilung.
entspricht also gerade der Breite der Gauss-Verteilung.
Um die Eigenschaften der Impulsverteilung des Teilchens zu bestimmen, berechnen
wir die Wellenfunktion 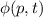 in der Impulsraumdarstellung. Mit Hilfe der
Fourier-Transformation (9.20) erhalten wir
in der Impulsraumdarstellung. Mit Hilfe der
Fourier-Transformation (9.20) erhalten wir
Die Ausführung der Integration liefert
Damit ergibt sich für die Wahrscheinlichkeitsdichte 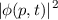 im Impulsraum
im Impulsraum
Der Erwartungswert 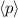 nimmt den Wert
nimmt den Wert
an, d.h. das Teilchen hat einen verschwindenden mittleren Impuls. Gleichzeitig ergibt
sich eine Impulsunschärfe 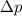 von
von
Mit (9.30) erhalten wir daraus für die Unschärferelation eines Gaussschen Wellenpakets
Das Gausssche Wellenpaket erfüllt somit gerade die minimale Unschärferelation (siehe Abschnitt 9.2.3).
Nachdem wir zwei Beispiele zur Unschärferelation betrachtet haben, kommen wir zur
Formulierung der Unschärferelation nach Heisenberg, wie sie 1927 aufgestellt wurde.
Wir schreiben sie hier für die Ortskoordinate  und die Impulskomponente
und die Impulskomponente
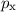
Für die allgemeine Formulierung und die Herleitung sei auf Anhang B oder weiterführende Literatur [11] verwiesen.
Wir erwähnen hier noch eine weitere Form der Heisenbergschen Unschärferelation, die sogenannte Energie-Zeit-Unschärferelation. Es gilt
Die Formulierung (9.38) sagt aus, dass die Energie 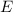 eines Systems, welches für die
Zeitspanne
eines Systems, welches für die
Zeitspanne 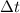 existiert, z.B. ein Atom dessen Lebensdauer im angeregten
Zustand durch
existiert, z.B. ein Atom dessen Lebensdauer im angeregten
Zustand durch 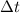 gegeben ist, nur auf
gegeben ist, nur auf 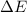 genau bestimmt ist. Diese
Relation legt zum Beispiel die Breite von spektralen Linien eines atomaren
Übergangs im Verhältnis zur Lebensdauer des angeregten Zustands des Atoms
fest.
genau bestimmt ist. Diese
Relation legt zum Beispiel die Breite von spektralen Linien eines atomaren
Übergangs im Verhältnis zur Lebensdauer des angeregten Zustands des Atoms
fest.
Operatoren spielen in der Quantenmechanik eine entscheidende Rolle. Denn jede
physikalische Grösse 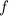 wird durch einen entsprechenden Operator
wird durch einen entsprechenden Operator 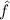 dargestellt.
Die Bedeutung von Operatoren im Rahmen der Quantenmechanik, besprechen wir in
diesem Abschnitt.
dargestellt.
Die Bedeutung von Operatoren im Rahmen der Quantenmechanik, besprechen wir in
diesem Abschnitt.
Wir beginnen mit einer Diskussion der Frage, wie sich der Erwartungswert des Impulses in der Ortsraumdarstellung berechnen lässt.
Wenn wir den Zustand des Teilchens durch die Wellenfunktion 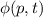 im
Impulsraum beschreiben, so lässt sich der Erwartungswert des Impulses
im
Impulsraum beschreiben, so lässt sich der Erwartungswert des Impulses 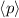 einfach
als Mittelwert von
einfach
als Mittelwert von 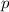 zur Wellenfunktion
zur Wellenfunktion 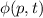 berechnen
berechnen
Wenn der Zustand des Teilchens aber durch die Wellenfunktion 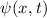 im Ortsraum
beschrieben wird, so muss folgender Erwartungswert
im Ortsraum
beschrieben wird, so muss folgender Erwartungswert
berechnet werden.
Hier stellt sich nun die Frage in welchem Zusammenhang der Impuls 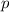 des Teilchens
mit der Wellenfunktion
des Teilchens
mit der Wellenfunktion 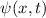 steht. Zur Lösung des Problems gehen wir von der
Impulsraumdarstellung aus und gehen dann durch die Fourier-Transformation auf die
Ortsraumdarstellung über. In einem ersten Schritt setzen wir für
steht. Zur Lösung des Problems gehen wir von der
Impulsraumdarstellung aus und gehen dann durch die Fourier-Transformation auf die
Ortsraumdarstellung über. In einem ersten Schritt setzen wir für 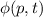 in (9.39)
die Fourier-Transformierte ein
in (9.39)
die Fourier-Transformierte ein
Wir schreiben das Integral über  mittels partieller Integration um
mittels partieller Integration um
Der erste Summand verschwindet, da 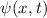 quadratisch integrabel (normierbar) ist
und somit insbesondere im Unendlichen gegen null strebt. Einsetzen in (9.41) und
Umformen liefert
quadratisch integrabel (normierbar) ist
und somit insbesondere im Unendlichen gegen null strebt. Einsetzen in (9.41) und
Umformen liefert
Wir kommen somit zu folgendem Schluss:
In der Ortsraumdarstellung, in der der Zustand eines Teilchens durch die
Wellenfunktion  beschrieben ist, wird der Erwartungswert des Impulses
beschrieben ist, wird der Erwartungswert des Impulses 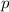 berechnet, indem man in (9.40) den Impuls
berechnet, indem man in (9.40) den Impuls 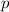 durch den Impulsoperator
durch den Impulsoperator
ersetzt.
Analog können wir nun auch den Erwartungswert der Ortskoordinate  in der
Impulsraumdarstellung berechnen. Wir gehen hier entsprechend von der
Ortsraumdarstellung aus und wechseln mittels Fourier-Transformation in die
Impulsraumdarstellung
in der
Impulsraumdarstellung berechnen. Wir gehen hier entsprechend von der
Ortsraumdarstellung aus und wechseln mittels Fourier-Transformation in die
Impulsraumdarstellung
Partielle Integration für das Integral über 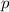 liefert
liefert
Der erste Summand verschwindet, da auch 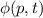 quadratisch integrabel
(normierbar) ist und somit insbesondere im Unendlichen gegen null strebt. Einsetzen
in (9.45) und Umformen liefert
quadratisch integrabel
(normierbar) ist und somit insbesondere im Unendlichen gegen null strebt. Einsetzen
in (9.45) und Umformen liefert
Wir fassen zusammen:
In der Impulsraumdarstellung, in der der Zustand eines Teilchens durch die
Wellenfunktion 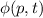 beschrieben ist, wird der Erwartungswert der Ortskoordinate
beschrieben ist, wird der Erwartungswert der Ortskoordinate
 berechnet, indem man die Ortskoordinate
berechnet, indem man die Ortskoordinate  in
in
durch den Ortsoperator
ersetzt.
In der Ortsraumdarstellung ist der Ortsoperator 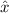 trivialerweise der Faktor
trivialerweise der Faktor  und
in der Impulsraumdarstellung ist der Impulsoperator
und
in der Impulsraumdarstellung ist der Impulsoperator 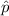 trivialerweise der Faktor
trivialerweise der Faktor 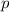 .
In Tab. 9.1 sind die Berechnungen für die Erwartungswerte für die Ortskoordinate
.
In Tab. 9.1 sind die Berechnungen für die Erwartungswerte für die Ortskoordinate
 und den Impuls
und den Impuls 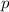 für die Orts- und Impulsraumdarstellung zusammengefasst. Es
ist zu bemerken, dass die Operatoren jeweils auf die nachfolgende Funktion wirken
und daher die Reihenfolge der Faktoren von entscheidender Bedeutung ist.
für die Orts- und Impulsraumdarstellung zusammengefasst. Es
ist zu bemerken, dass die Operatoren jeweils auf die nachfolgende Funktion wirken
und daher die Reihenfolge der Faktoren von entscheidender Bedeutung ist.
| Ortsraumdarstellung | Impulsraumdarstellung |
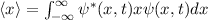 | 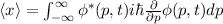 |
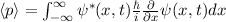 | 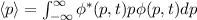 |
 und
den Impuls
und
den Impuls 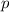 in Orts- und Impulsraumdarstellung.
in Orts- und Impulsraumdarstellung.Entsprechend zu den vorangegangenen Berechnungen in diesem Abschnitt kön-nen
auch die Erwartungswerte von Potenzen der Ortskoordinate  und des Impulses
und des Impulses 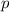 berechnet werden. Es ergibt sich für den Erwartungswert von Potenzen von
berechnet werden. Es ergibt sich für den Erwartungswert von Potenzen von 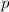 in der
Ortsraumdarstellung
in der
Ortsraumdarstellung
und entsprechend für den Erwartungswert von Potenzen von  in der
Impulsraumdarstellung
in der
Impulsraumdarstellung
Bei der Betrachtung von weiteren Beispielen von Operatoren beschränken wir uns auf die Ortsraumdarstellung.
Wie wir im letzten Abschnitt gesehen haben, ist der Ortsoperator 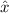 in
Ortsraumdarstellung gleich dem Faktor
in
Ortsraumdarstellung gleich dem Faktor  . Entsprechend gilt in drei Dimensionen
für den Ortsoperator
. Entsprechend gilt in drei Dimensionen
für den Ortsoperator 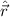 die folgende einfache Darstellung
die folgende einfache Darstellung
Beschreiben wir die Bewegung eines Teilchens im dreidimensionalen Raum in
kartesischen Koordinaten, dann ist jeder Impulskomponente ein Operator zugeordnet.
Nach (9.44) gilt für die Operatoren 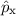 ,
, 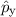 und
und 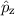 der Impulskomponenten
der Impulskomponenten
Dem Impulsvektor 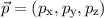 ist also ein Impulsoperator
ist also ein Impulsoperator 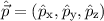 zugeordnet. Wenn man ihn auf eine Wellenfunktion anwendet, so resultiert ein
Vektor.
zugeordnet. Wenn man ihn auf eine Wellenfunktion anwendet, so resultiert ein
Vektor.
Die Erwartungswerte der Impulskomponenten 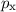 ,
, 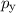 und
und 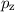 lassen sich
berechnen durch
lassen sich
berechnen durch
Aus der klassischen Mechanik ist die Hamilton-Funktion 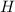 bekannt. Sie
entspricht der Gesamtenergie
bekannt. Sie
entspricht der Gesamtenergie 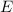 eines Systems ausgedrückt als Funktion der
verallgemeinerten Koordinaten
eines Systems ausgedrückt als Funktion der
verallgemeinerten Koordinaten 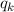 und der dazu kanonisch konjugierten Impulse
und der dazu kanonisch konjugierten Impulse
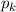 . Der Hamilton-Operator
. Der Hamilton-Operator 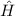 ist die zugehörige quantenmechanische
Grösse.
ist die zugehörige quantenmechanische
Grösse.
Wir betrachten als Beispiel die Bewegung eines Teilchens der Masse 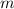 mit den
kartesischen Koordinaten
mit den
kartesischen Koordinaten  ,
, 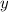 und
und  im Potential
im Potential 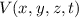 . Die konjugierten
Impulse sind demzufolge die kartesischen Impulskomponenten
. Die konjugierten
Impulse sind demzufolge die kartesischen Impulskomponenten 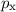 ,
, 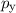 und
und 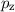 . Wir
beschränken uns hier auf eine nichtrelativistische Betrachtung. Klassisch gelten die
folgenden Beziehungen
. Wir
beschränken uns hier auf eine nichtrelativistische Betrachtung. Klassisch gelten die
folgenden Beziehungen
Damit lässt sich die kinetische Energie 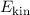 schreiben als
schreiben als
Die entsprechende Hamilton-Funktion 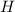 lautet somit
lautet somit
Den entsprechenden Hamilton-Operator 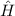 in Ortsraumdarstellung erhalten wir,
indem wir die Impulskomponenten
in Ortsraumdarstellung erhalten wir,
indem wir die Impulskomponenten 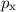 ,
, 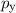 und
und 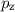 durch die entsprechenden
Impulsoperatoren
durch die entsprechenden
Impulsoperatoren 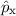 ,
, 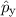 und
und 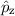 in Ortsraumdarstellung ersetzen. Mit (9.53),
(9.54) und (9.55) ergibt sich somit für den Hamilton-Operator
in Ortsraumdarstellung ersetzen. Mit (9.53),
(9.54) und (9.55) ergibt sich somit für den Hamilton-Operator 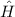
wobei 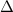 den Laplace-Operator bezeichnet. Die potentielle Energie
den Laplace-Operator bezeichnet. Die potentielle Energie 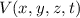 ist
kein Differentialoperator, da sie die Impulskomponenten nicht enthält. Sie wirkt als
Faktor.
ist
kein Differentialoperator, da sie die Impulskomponenten nicht enthält. Sie wirkt als
Faktor.
Der Erwartungswert der Hamilton-Funktion 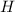 ist gegeben durch
ist gegeben durch
Der (klassische) Bahndrehimpulsvektor 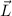 eines Teilchens bzgl. des Ursprungs ist
definiert als
eines Teilchens bzgl. des Ursprungs ist
definiert als
wobei 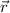 den Ortsvektor und
den Ortsvektor und 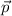 den Impulsvektor bezeichnen. Zum
Bahndrehimpulsoperator gelangen wir nun, indem wir für jede Impulskomponente
den entsprechenden Operator einsetzen. Die Ortskoordinaten bleiben als Faktoren
stehen, da wir in der Ortsraumdarstellung rechnen. Es gilt
den Impulsvektor bezeichnen. Zum
Bahndrehimpulsoperator gelangen wir nun, indem wir für jede Impulskomponente
den entsprechenden Operator einsetzen. Die Ortskoordinaten bleiben als Faktoren
stehen, da wir in der Ortsraumdarstellung rechnen. Es gilt
Beim Wasserstoffatom bewegt sich das Elektron im Zentralpotential des Kerns
(siehe Kapitel 11). Es zeigt sich, dass diese Bewegung eines Teilchens im
Zentralpotential einfachheitshalber in Kugelkoordinaten behandelt wird. Aus
diesem Grund geben wir hier den Bahndrehimpulsoperator zusätzlich auch in
Kugelkoordinaten an. Man erhält für den Bahndrehimpulsoperator 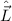 in
Kugelkoordinaten
in
Kugelkoordinaten
Wir beweisen die Richtigkeit dieses Ausdrucks indem wir auf die kartesischen Koordinaten zurückrechnen. Die Umrechnung zwischen kartesischen Koordinaten und Kugelkoordinaten lautet (siehe Abb. 9.4)
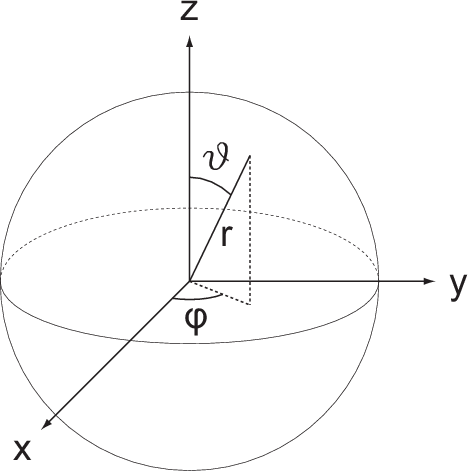
 ,
, 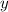 ,
,  und den Kugelkoordinaten
und den Kugelkoordinaten  ,
, 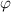 ,
, 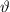 .
. auf
auf 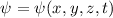 erhalten wir
erhalten wir 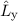 gilt
gilt 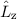 gilt
gilt Diese Ausdrücke stimmen mit (9.67) überein, womit die Richtigkeit von (9.68) bewiesen ist.
Das Plancksche Wirkungsquantum 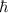 hat die Dimension des Bahndrehimpulses. In
der Quantenmechanik wird deshalb der Bahndrehimpuls oft in Einheiten von
hat die Dimension des Bahndrehimpulses. In
der Quantenmechanik wird deshalb der Bahndrehimpuls oft in Einheiten von 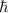 angegeben, sodass in den Formeln für den Bahndrehimpuls der Faktor
angegeben, sodass in den Formeln für den Bahndrehimpuls der Faktor 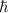 entfällt.
entfällt.
Wir haben bisher an diversen Beispielen erörtert, wie eine physikalische
Grösse 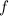 in der Quantenmechanik durch einen entsprechenden Operator
in der Quantenmechanik durch einen entsprechenden Operator
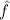 dargestellt wird. In Tab. 9.2 sind die kennengelernten Operatoren in
der Ortsraumdarstellung nochmals zusammengefasst. Wir definieren nun
zum Abschluss dieses Abschnitts allgemein was man unter einem Operator
in der Quantenmechanik versteht und gehen auf seine Eigenschaften ein.
dargestellt wird. In Tab. 9.2 sind die kennengelernten Operatoren in
der Ortsraumdarstellung nochmals zusammengefasst. Wir definieren nun
zum Abschluss dieses Abschnitts allgemein was man unter einem Operator
in der Quantenmechanik versteht und gehen auf seine Eigenschaften ein.
| Physikalische Grösse | klassisch | Operator |
| Ortsvektor | 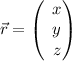 | 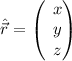 |
| Impulsvektor | 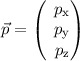 | 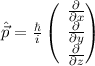 |
| Hamilton-Funktion | 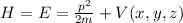 | 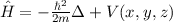 |
| Bahndrehimpulsvektor |  | 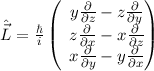 |
Definition 9.5 Ein quantenmechanischer Operator 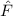 ist definiert durch die
Bedingung, dass für eine Funktion
ist definiert durch die
Bedingung, dass für eine Funktion 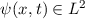 gilt
gilt
Dabei bezeichnet 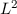 den Raum der quadratisch integrablen Funktionen (siehe
Definition 9.1).
den Raum der quadratisch integrablen Funktionen (siehe
Definition 9.1).
Quantenmechanische Operatoren besitzten folgende Eigenschaften:
Eine erste Eigenschaft quantenmechanischer Operatoren ist die Linearität:
Quantenmechanische Operatoren erfüllen zudem das Distributivgesetz.
Quantenmechanische Operatoren erfüllen ebenfalls das Assoziativgesetz.
Quantenmechanische Operatoren kommutieren im Allgemeinen nicht. Bevor wir die Definition des Kommutativgesetzes angeben, führen wir den Begriff des Kommutators ein.
Mit Hilfe dieser Definition 9.9 formulieren wir das Kommutativgesetz.
Definition 9.10 Zwei Operatoren 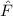 und
und 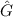 kommutieren falls der
entsprechende Kommutator verschwindet, d.h.
kommutieren falls der
entsprechende Kommutator verschwindet, d.h.
Ist der Kommutator ungleich null, so kommutieren die beiden Operatoren nicht.
Wir betrachten dazu einige Beispiele. Als erstes betrachten wir die zu
den Funktionen 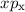 und
und 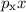 gehörenden Operatoren
gehörenden Operatoren 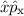 und
und
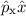 in der Ortsraumdarstellung. Anwendung auf
in der Ortsraumdarstellung. Anwendung auf 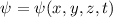 ergibt
ergibt
Damit folgt
Diese Gleichung gilt unabhängig von der Wellenfunktion 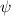 , auf welche die
Operatoren wirken. D.h. für den Kommutator der beiden Operatoren
, auf welche die
Operatoren wirken. D.h. für den Kommutator der beiden Operatoren 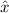 und
und
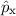 gilt
gilt
In diesem Beispiel verschwindet der Kommutator nicht, d.h. die beiden
Operatoren 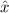 und
und 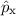 kommutieren nicht. Es sei bemerkt, dass die
Operatorgleichung (9.85) ganz allgemein für kanonisch konjugierte Variablen
gilt.
kommutieren nicht. Es sei bemerkt, dass die
Operatorgleichung (9.85) ganz allgemein für kanonisch konjugierte Variablen
gilt.
Im Gegensatz gibt es auch Operatoren, deren Kommutator verschwindet. Zum
Beispiel gilt für die Anwendung der Operatoren 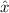 und
und 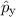 auf die
Wellenfunktion
auf die
Wellenfunktion 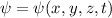 in der Ortsraumdarstellung
in der Ortsraumdarstellung
Das Nichtverschwinden eines Kommutators hat (wie wir in Abschnitt 9.5.4 präzisieren und beweisen werden) folgende Bedeutung: Die Erwartungswerte nicht kommutierender Operatoren können nicht gleichzeitig mit beliebiger Genauigkeit bestimmt werden.
Diese Eigenschaft ist, wie wir auch im Zusammenhang mit der Heisenbergschen
Unschärferelation (siehe Abschnitt 9.2) gesehen haben, ein wichtiger
Aspekt der Quantenmechanik. In der klassischen Physik beobachten wir
dieses Phänomen nie: Klassische Messgrössen kommutieren immer
und sind dementsprechend gleichzeitig beliebig genau bestimmbar. Es
fällt jedoch auf, dass der Kommutator der Operatoren  und
und 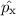 für
für
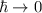 verschwindet. In diesem Grenzfall können dann
verschwindet. In diesem Grenzfall können dann  und
und 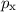 beliebig genau bestimmt werden. In diesem Grenzfall strebt auch die de
Broglie-Wellenlänge
beliebig genau bestimmt werden. In diesem Grenzfall strebt auch die de
Broglie-Wellenlänge 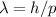 gegen null, so dass keine Beugungserscheinungen
mehr auftreten. Insbesondere verschwindet auch die rechte Seite der
Heisenbergschen Unschärferelation (9.37). Aus diesen Gründen kann die
klassische Mechanik als Grenzfall der Quantenmechanik für
gegen null, so dass keine Beugungserscheinungen
mehr auftreten. Insbesondere verschwindet auch die rechte Seite der
Heisenbergschen Unschärferelation (9.37). Aus diesen Gründen kann die
klassische Mechanik als Grenzfall der Quantenmechanik für 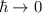 betrachtet
werden.
betrachtet
werden.
Am Beispiel der verschiedenen Komponenten des Bahndrehimpulses zeigt
sich, dass nicht nur Operatoren, die kanonisch konjugierten Variablen
entsprechen, nicht kommutieren. Für die Anwendung des Kommutators der
Operatoren 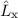 und
und 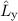 auf die Wellenfunktion
auf die Wellenfunktion 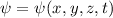 erhält
man
erhält
man
Analog ergibt sich
Dies bedeutet, dass es nicht möglich ist, dass zwei verschiedene Komponenten des Bahndrehimpulses gleichzeitig beliebig genau bestimmt werden können.
Operatoren in der Quantenmechanik haben reelle Erwartungswerte, da physikalisch messbare Grössen, sogenannte Observable2, reell sind. Beispiele für Observable sind Ortskoordinaten, Impuls, Bahndrehimpuls, Energie oder allgemein reelle Funktionen von Orts- und Impulskoordinaten.
Ein Operator 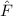 , der einer Observablen
, der einer Observablen 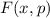 entspricht, muss demzufolge
folgende Bedingung erfüllen
entspricht, muss demzufolge
folgende Bedingung erfüllen
d.h. der Erwartungswert muss gleich seinem konjugiert Komplexen sein. Für
den Operator 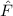 gilt daher
gilt daher
Operatoren, die diese Bedingung erfüllen, werden nach Charles Hermite hermitesche oder selbstadjungierte Operatoren genannt. Es ergibt sich also folgende Schlussfolgerung:
Jeder Observablen 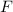 entspricht ein hermitescher Operator
entspricht ein hermitescher Operator 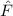 .
.
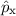 zur Observablen
zur Observablen 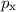 und
zeigen, dass
und
zeigen, dass 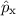 hermitesch ist. Es gilt
hermitesch ist. Es gilt womit gezeigt ist, dass der Impulsoperator 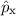 hermitesch ist. PI steht für
partielle Integration.
hermitesch ist. PI steht für
partielle Integration.
Es stellt sich heraus, dass Operatoren zu Observablen nicht automatisch
hermitesch sind. Als Beispiel betrachten wir dazu die Funktionen 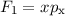 und
und 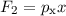 . Sie sind als Produkt aus Ortskoordinate und Impuls
physikalisch deutbare Funktionen und demzufolge Observablen. Die
Berechnung der Erwartungswerte
. Sie sind als Produkt aus Ortskoordinate und Impuls
physikalisch deutbare Funktionen und demzufolge Observablen. Die
Berechnung der Erwartungswerte 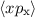 und
und 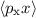 zeigt jedoch,
dass weder der Operator
zeigt jedoch,
dass weder der Operator 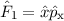 noch der Operator
noch der Operator 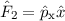 hermitesch ist. Zudem erhält man für
hermitesch ist. Zudem erhält man für 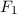 und
und 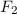 unterschiedliche
Erwartungswerte.
unterschiedliche
Erwartungswerte.
Es ist jedoch möglich, diese Operatoren zu „hermitesieren“. In unserem Beispiel
ist die Hermitesierung relativ einfach: Der zu 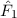 und
und 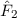 gehörende
hermitesche Operator lautet
gehörende
hermitesche Operator lautet
Im Allgemeinen kann diese Aufgabe der Hermitesierung jedoch relativ kompliziert sein.
Ist die Wellenfunktion 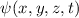 eines Teilchens bekannt, so ist der Zustand des
Teilchens vollständig charakterisiert. Insbesondere ist es möglich die Erwartungswerte
beliebiger Observablen auszurechnen und somit das Verhalten des Teilchens in einem
Experiment vorauszusagen. Es stellt sich nun die Frage: Wie bestimmt man die
Wellenfunktion
eines Teilchens bekannt, so ist der Zustand des
Teilchens vollständig charakterisiert. Insbesondere ist es möglich die Erwartungswerte
beliebiger Observablen auszurechnen und somit das Verhalten des Teilchens in einem
Experiment vorauszusagen. Es stellt sich nun die Frage: Wie bestimmt man die
Wellenfunktion 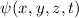 eines Teilchens?
eines Teilchens?
Die Antwort auf diese Frage lieferte Schrödinger im Jahr 1926:
Postulat 2 Die Wellenfunktion 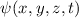 ist eine Lösung der Differentialgleichung
ist eine Lösung der Differentialgleichung
Diese Gleichung wird nach Schrödinger die zeitabhängige Schrödinger-Gleichung genannt.
Die Dynamik eines quantenmechanischen Systems wird durch die zeitab-hängige Schrödinger-Gleichung bestimmt. Die Schrödinger-Gleichung ist ein weiteres Postulat der Quantenmechanik und kann nicht hergeleitet oder bewiesen werden.
Für ein Teilchen der Masse 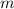 , das sich mit nichtrelativistischer Geschwindigkeit in
einem Potential
, das sich mit nichtrelativistischer Geschwindigkeit in
einem Potential 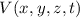 bewegt, nimmt die zeitabhängige Schrö-dinger-Gleichung
mit (9.64) folgende Form an
bewegt, nimmt die zeitabhängige Schrö-dinger-Gleichung
mit (9.64) folgende Form an
In der Quantenmechanik tritt die Schrödinger-Gleichung an die Stelle der Newtonschen Bewegungsgleichung der klassischen Mechanik. Wir verdeutlichen diesen Zusammenhang hier an einem Beispiel.
Ein Teilchen der Masse 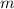 bewege sich entlang der x-Achse in einem Potential
bewege sich entlang der x-Achse in einem Potential
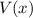 . Die Newtonsche Bewegungsgleichung kann geschrieben werden in der
Form
. Die Newtonsche Bewegungsgleichung kann geschrieben werden in der
Form
Die Quantenmechanik erlaubt nur statistische Aussagen in Form von berechneten Erwartungswerten. Demzufolge würde die entsprechende Gleichung in der Quantenmechanik folgende Gestalt annehmen
Herleitung:
Die Schrödinger-Gleichung und das konjugiert Komplexe der Schrödinger-Glei-chung für unser Beispiel lauten
Einsetzen in (9.98) liefert
Wir betrachten ein Teilchen der Masse 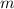 , das sich mit nichtrelativistischer
Geschwindigkeit in einem Potential
, das sich mit nichtrelativistischer
Geschwindigkeit in einem Potential 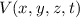 bewegt.
bewegt.
Definition 9.11 Ein Zustand, der dadurch gekennzeichnet ist, dass die
Wahrscheinlichkeit 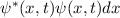 das Teilchen zwischen
das Teilchen zwischen  und
und 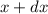 anzutreffen nicht von der Zeit
anzutreffen nicht von der Zeit 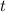 abhängt, heisst stationärer Zustand.
abhängt, heisst stationärer Zustand.
Ein Beispiel dafür ist die bereits mehrfach erwähnte ebene, harmonische Materiewelle
Allgemein hat ein stationärer Zustand die Form
In drei Dimensionen gilt
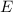 ist die totale Energie des Teilchens, welche bei nichtrelativistischer Behandlung
die Summe aus kinetischer und potentieller Energie ist
ist die totale Energie des Teilchens, welche bei nichtrelativistischer Behandlung
die Summe aus kinetischer und potentieller Energie ist
Wir setzen nun den Ansatz (9.104) in die zeitabhängige Schrödinger-Gleich-ung (9.94) ein, um herauszufinden, unter welchen Bedingungen sie eine Lösung ist
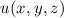 ist eine Funktion der Ortskoordinaten allein, sodass
ist eine Funktion der Ortskoordinaten allein, sodass
Wenn sich das Teilchen in einem zeitunabhängigen Potential 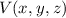 bewegt und
somit die Gesamtenergie
bewegt und
somit die Gesamtenergie 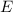 konstant ist (
konstant ist (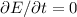 ) gilt
) gilt
Diese Gleichung bestimmt die zeitunabhängige Funktion 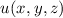 .
.
Ein Teilchen ist also in einem stationären Zustand, wenn seine Bewegung in einem
zeitlich konstanten Potential 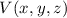 stattfindet. Für die Funktion
stattfindet. Für die Funktion 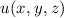 gilt
dann die zeitunabhängige Schrödinger-Gleichung
gilt
dann die zeitunabhängige Schrödinger-Gleichung
Lösungen der Schrödinger-Gleichung in einer Dimension besitzen folgende Eigenschaften (gelten auch in drei Dimensionen):
Bei physikalischen Problemen müssen die Lösungen 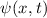 normierbar
sein
normierbar
sein
Da die Schrödinger-Gleichung linear und homogen ist, darf man eine Lösung mit einem Normierungsfaktor multiplizieren. In Übereinstimmung mit (9.2) wählen wir den Normierungsfaktor jeweils so, dass
Im Fall stationärer Zustände ist 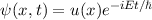 , so dass
, so dass
Aus der Normierungsbedingung folgt, dass 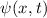 und
und 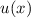 mit
mit 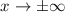 genügend rasch gegen null streben müssen. Dasselbe gilt auch für die
Ableitungen nach
genügend rasch gegen null streben müssen. Dasselbe gilt auch für die
Ableitungen nach  .
.
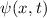 und
und 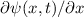 müssen für alle
müssen für alle  stetig, eindeutig und endlich sein.
Dasselbe gilt auch für
stetig, eindeutig und endlich sein.
Dasselbe gilt auch für 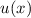 und
und 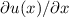 .
.
Diese Eigenschaften garantieren zum Beispiel, dass die Aufenthaltswahrscheinlichkeit und der Impuls eines Teilchens kontinuierlich mit den Koordinaten variieren.
Da die Schrödinger-Gleichung linear und homogen ist, ist eine beliebige
Linearkombination von Lösungen ebenfalls eine Lösung. D.h. sind zum Beispiel
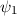 und
und 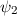 Lösungen der Schrödinger-Gleichung, so ist
Lösungen der Schrödinger-Gleichung, so ist 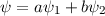 ebenfalls eine Lösung.
ebenfalls eine Lösung.
Es kommt vor, dass idealisierte Beispiele und Grenzfälle einige dieser Eigenschaften nicht erfüllen. Wir geben hier zwei bekannte Beispiele an:
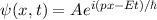 erfüllt die
Normierungsbedingung und das geforderte Verhalten im Unendlichen
nicht. Dies entspricht dem Grenzfall, bei dem Teilchen vollständig im
Raum delokalisiert sind, ihre Position also völlig unbestimmt ist.
erfüllt die
Normierungsbedingung und das geforderte Verhalten im Unendlichen
nicht. Dies entspricht dem Grenzfall, bei dem Teilchen vollständig im
Raum delokalisiert sind, ihre Position also völlig unbestimmt ist.
Wir berechnen nun Lösungen der Schrödinger-Gleichung für einige grundlegende physikalische Probleme.
Wir betrachten ein nichtrelativistisches Teilchen, das sich längs der x-Achse bewegen
kann und dessen potentielle Energie 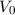 räumlich und zeitlich konstant ist. Nach der
klassischen Mechanik bewegt sich das Teilchen dann mit einem beliebigen, konstanten
Impuls von links nach rechts oder von rechts nach links oder es bleibt irgendwo in
Ruhe. Wir wollen nun herausfinden wie ein solches Problem quantenmechanisch
gelöst wird.
räumlich und zeitlich konstant ist. Nach der
klassischen Mechanik bewegt sich das Teilchen dann mit einem beliebigen, konstanten
Impuls von links nach rechts oder von rechts nach links oder es bleibt irgendwo in
Ruhe. Wir wollen nun herausfinden wie ein solches Problem quantenmechanisch
gelöst wird.
Da das Potential 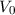 zeitunabhängig ist, kommt die zeitunabhängige
Schröd-inger-Gleichung (9.109) zur Anwendung
zeitunabhängig ist, kommt die zeitunabhängige
Schröd-inger-Gleichung (9.109) zur Anwendung
Wir wählen den folgenden Ansatz
Einsetzen in (9.113) liefert
Daraus ergibt sich
Somit nimmt die Funktion 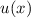 folgende Form an
folgende Form an
Die vollständige Wellenfunktion 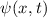 lautet
lautet
Mit 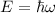 und
und 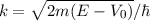 ist
ist 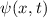 die Superposition einer links-
mit einer rechtslaufenden harmonischen Welle
die Superposition einer links-
mit einer rechtslaufenden harmonischen Welle
Nach de Broglie gilt 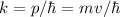 und mit
und mit 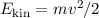 gilt
gilt 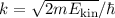 .
Der Vergleich mit (9.116) führt auf
.
Der Vergleich mit (9.116) führt auf 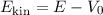 , was bestätigt, dass
, was bestätigt, dass 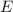 der
Gesamtenergie des Teilchens entspricht. Für die Wellenfunktion
der
Gesamtenergie des Teilchens entspricht. Für die Wellenfunktion 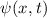 eines
Teilchens mit konstantem längs der positiven x-Achse gerichteten Impuls
eines
Teilchens mit konstantem längs der positiven x-Achse gerichteten Impuls 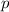 gilt
dementsprechend
gilt
dementsprechend
Die Wahrscheinlichkeitsdichte 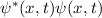 nimmt dabei den konstanten Wert
nimmt dabei den konstanten Wert
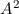 an. Demzufolge ist diese Wellenfunktion nicht normierbar. In diesem Fall kann
die Konstante
an. Demzufolge ist diese Wellenfunktion nicht normierbar. In diesem Fall kann
die Konstante 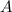 so gewählt werden, dass sie die konstante Dichte der Teilchen
entlang der
so gewählt werden, dass sie die konstante Dichte der Teilchen
entlang der  -Koordinate angibt.
-Koordinate angibt.
Wir lösen nun das in Abschnitt 9.1.1 besprochene physikalische Problem eines
Teilchens in einem Potentialtopf mit der Schrödinger-Gleichung. D.h. wir betrachten
ein Teilchen der Masse 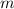 , das sich längs der x-Achse bewegt, jedoch zwischen den
Koordinaten
, das sich längs der x-Achse bewegt, jedoch zwischen den
Koordinaten 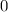 und
und 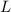 lokalisiert ist. Das Potential V(x) hat dementsprechend die
Form (siehe Abb. 9.1)
lokalisiert ist. Das Potential V(x) hat dementsprechend die
Form (siehe Abb. 9.1)
Da das Potential zeitunabhängig ist, gilt die zeitunabhängige Schrödinger-Glei-chung
Für 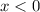 und
und 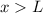 ist wegen
ist wegen 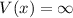
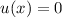 . Für
. Für 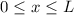 nimmt die
zeitunabhängige Schrödinger-Gleichung folgende Form an
nimmt die
zeitunabhängige Schrödinger-Gleichung folgende Form an
Wir wählen wieder den Ansatz
Einsetzen in 9.123 liefert
Daraus ergibt sich
Somit nimmt die Funktion 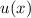 folgende Form an
folgende Form an
wobei 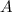 und
und 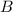 die Amplituden der rechts bzw. links laufenden
Wellen beschreiben. Die Berücksichtigung der Randbedingungen führt
analog zu den Ausführungen in Abschnitt 9.1.1 auf die folgende
Lösung3
die Amplituden der rechts bzw. links laufenden
Wellen beschreiben. Die Berücksichtigung der Randbedingungen führt
analog zu den Ausführungen in Abschnitt 9.1.1 auf die folgende
Lösung3
wobei die (diskreten) Energiewerte 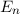 gegeben sind durch
gegeben sind durch
Die Wellenfunktionen (9.128) erfüllen nicht alle Bedingungen, die man an eine
Lösung der Schrödinger-Gleichung stellt, denn die Ableitung der Wellenfunktion nach
 bei
bei 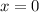 und
und 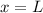 ist unstetig. Dies ist eine Folge davon, dass das
betrachtete Potential zu unphysikalischen Randbedingungen führt. Wie wir im
nächsten Abschnitt sehen werden, tritt diese Schwierigkeit beim Potentialtopf mit
endlicher tiefe
ist unstetig. Dies ist eine Folge davon, dass das
betrachtete Potential zu unphysikalischen Randbedingungen führt. Wie wir im
nächsten Abschnitt sehen werden, tritt diese Schwierigkeit beim Potentialtopf mit
endlicher tiefe 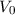 nicht auf. Trotzdem sind die Wellenfunktionen (9.128) durchaus
sinnvoll, wenn man sie als Grenzfall
nicht auf. Trotzdem sind die Wellenfunktionen (9.128) durchaus
sinnvoll, wenn man sie als Grenzfall 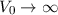 betrachtet.
betrachtet.
Wir kommen nun vom Spezialfall 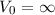 zum allgemeinen Fall
zum allgemeinen Fall 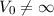 . Wir
betrachten ein Teilchen mit Masse
. Wir
betrachten ein Teilchen mit Masse 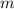 , das sich in einem zeitlich konstanten
Potential
, das sich in einem zeitlich konstanten
Potential
welches die Gestalt eines symmetrischen Topfes der Tiefe 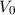 hat (siehe Abb. 9.5),
bewegt. Die Gesamtenergie des Teilchens sei
hat (siehe Abb. 9.5),
bewegt. Die Gesamtenergie des Teilchens sei 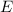 .
.
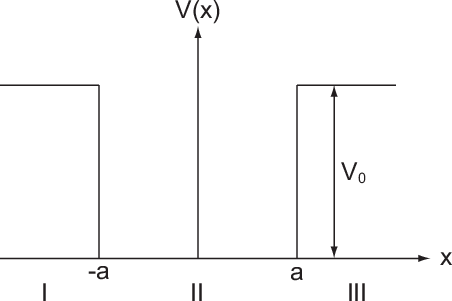
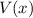 in Abhängigkeit von
in Abhängigkeit von  für ein Teilchen
im endlichen Potentialtopf. Die x-Achse wird für die Berechnungen in drei
Teilgebiete I, II und III unterteilt.
für ein Teilchen
im endlichen Potentialtopf. Die x-Achse wird für die Berechnungen in drei
Teilgebiete I, II und III unterteilt.Wir betrachten zuerst die klassischen Erwartungen und unterscheiden dabei die Fälle
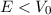 und
und 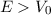 :
:
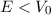 : Da die kinetische Energie positiv sein muss, kann sich das
Teilchen nur innerhalb des Topfes aufhalten. Es bewegt sich zwischen den
Umkehrpunkten
: Da die kinetische Energie positiv sein muss, kann sich das
Teilchen nur innerhalb des Topfes aufhalten. Es bewegt sich zwischen den
Umkehrpunkten 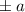 hin und her.
hin und her.
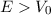 : Das Teilchen kann den Topf durchqueren und sich auch
ausserhalb desselben aufhalten.
: Das Teilchen kann den Topf durchqueren und sich auch
ausserhalb desselben aufhalten.Wir kommen nun zur quantenmechanischen Behandlung für den Fall dass
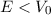 , d.h. wenn das Teilchen im Potentialtopf lokalisiert ist. Wir unterteilen
die x-Achse in drei Bereiche I, II und III (siehe Abb. 9.5) für die wir die
zeitunabhängige (Potential ist zeitunabhängig) Schrödinger-Gleichung separat
lösen.
, d.h. wenn das Teilchen im Potentialtopf lokalisiert ist. Wir unterteilen
die x-Achse in drei Bereiche I, II und III (siehe Abb. 9.5) für die wir die
zeitunabhängige (Potential ist zeitunabhängig) Schrödinger-Gleichung separat
lösen.
 an und daher lautet die
zeitunabhängige Schrödinger-Gleichung
an und daher lautet die
zeitunabhängige Schrödinger-Gleichung Die Lösung dieser Gleichung ist
Da die Lösung für  endlich sein muss gilt
endlich sein muss gilt 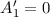 und wir
erhalten
und wir
erhalten
Die Lösung dieser Gleichung ist
Aus den Stetigkeitsbedingungen für die Wellenfunktion und deren Ableitung nach  an den Stellen
an den Stellen 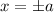 ergeben sich die folgenden Gleichungen zur Bestimmung der
Amplituden und Energiewerte
ergeben sich die folgenden Gleichungen zur Bestimmung der
Amplituden und Energiewerte
In Matrixschreibweise lautet dieses Gleichungssystem
Elementare Zeilenumformungen für lineare Gleichungssysteme liefern
Nichttriviale Lösungen ergeben sich für det = 0. Daraus ergibt sich
= 0. Daraus ergibt sich
Wir unterscheiden hier zwei Fälle
die symmetrischen (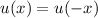 ) und antisymmetrischen (
) und antisymmetrischen (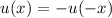 )
Wellenfunktionen entsprechen. Wir berechnen separat die Amplituden der
Wellenfunktionen in den drei Regionen und die sich daraus ergebenden möglichen
Energiewerte.
)
Wellenfunktionen entsprechen. Wir berechnen separat die Amplituden der
Wellenfunktionen in den drei Regionen und die sich daraus ergebenden möglichen
Energiewerte.
Wir setzen  und bestimmen mit (9.142) schrittweise die weiteren
Amplituden. Für
und bestimmen mit (9.142) schrittweise die weiteren
Amplituden. Für  erhalten wir mit (9.144)
erhalten wir mit (9.144)
Wir erhalten also für den ersten Fall für den Bereich II antisymmetrische
Wellenfunktionen. Daher nennen wir diesen Fall antisymmetrisch. Für  und
und
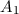 ergibt sich
ergibt sich
Die Wellenfunktionen für die drei Bereiche I, II und III nehmen dementsprechend die folgende Form an
Die verbleibende Unbekannte 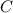 erhalten wir aus der Normierungsbedingung.
Es gilt
erhalten wir aus der Normierungsbedingung.
Es gilt
Daraus ergibt sich für die Konstante 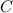
Damit ist die Wellenfunktion für das Teilchen im endlichen Potentialtopf im antisymmetrischen Fall bestimmt.
Es bleibt noch die Frage zu klären, welche Energiewerte für das Teilchen
erlaubt sind. Wir formen dazu die Gleichung (9.144) um, sodass wir eine
transzendente Gleichung erhalten, die wir graphisch lösen können. In einem
ersten Schritt ersetzen wir 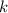 und
und 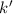 in (9.144) durch die Ausdrücke
in (9.133) und (9.135). Wir erhalten somit
in (9.144) durch die Ausdrücke
in (9.133) und (9.135). Wir erhalten somit
Wir schreiben nun auch die linke Seite der Gleichung als Summe von Real-und Imaginärteil
Gleichsetzen der Real- bzw. Imaginärteile ergibt folgendes Gleichungssystem
Wir benützen die Additionstheoreme 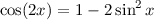 und
und
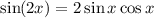 und erhalten
und erhalten
Division von (9.159) durch (9.158) ergibt
Wir führen nun die Konstante  ein. Damit ergibt sich das
folgende Resultat (siehe Gl. (9.135))
ein. Damit ergibt sich das
folgende Resultat (siehe Gl. (9.135))
Dies ist die zu Beginn erwähnte transzendente Gleichung, die wir nun
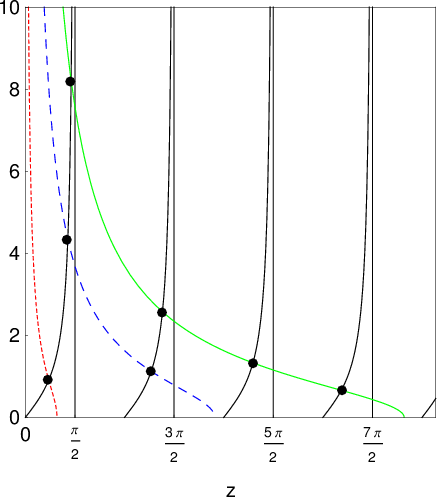
graphisch lösen. Dazu setzen wir  und tragen die Funktionen
und tragen die Funktionen
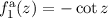 und
und 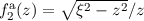 auf (siehe Abb. 9.6).
auf (siehe Abb. 9.6).
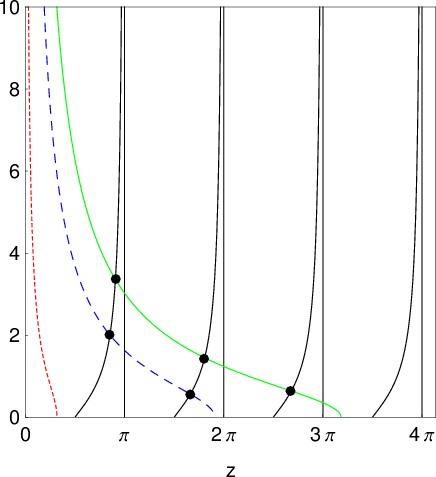
 . Die Funktion
. Die Funktion 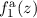 entspricht der schwarzen
durchgezogenen Linie, die Funktion
entspricht der schwarzen
durchgezogenen Linie, die Funktion 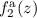 ist durch die rot gepunktete (
ist durch die rot gepunktete (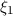 ),
blau gestrichelte (
),
blau gestrichelte (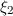 ) und grün durchgezogene Linie (
) und grün durchgezogene Linie (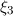 ) dargestellt, wobei
) dargestellt, wobei
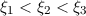 .
.Die erlaubten Werte von  ergeben sich aus den Schnittpunkten dieser beiden
Kurven. Die Anzahl antisymmetrischer Lösungen
ergeben sich aus den Schnittpunkten dieser beiden
Kurven. Die Anzahl antisymmetrischer Lösungen 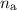 hängt von
hängt von 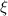 ab. Dabei
gilt folgende Gesetzmässigkeit: Wenn
ab. Dabei
gilt folgende Gesetzmässigkeit: Wenn
dann besitzt (9.161) genau 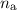 Lösungen. Insbesondere wird daraus
ersichtlich, dass antisymmetrische Lösungen nur dann existieren, wenn
Lösungen. Insbesondere wird daraus
ersichtlich, dass antisymmetrische Lösungen nur dann existieren, wenn
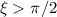 , d.h. wenn gilt
, d.h. wenn gilt
Das Potential 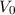 muss also einen minimalen Wert aufweisen. Die
muss also einen minimalen Wert aufweisen. Die  entsprechenden Energiewerte
entsprechenden Energiewerte 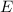 ergeben sich aus (siehe Gl. (9.135))
ergeben sich aus (siehe Gl. (9.135))
Da der symmetrische Fall analog zum antisymmetrische Fall gelöst wird,
werden wir uns im Wesentlichen auf die Angabe der Resultate beschränken.
Wir setzen wiederum 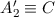 und bestimmen mit (9.142) schrittweise die
weiteren Amplituden. Für
und bestimmen mit (9.142) schrittweise die
weiteren Amplituden. Für 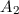 erhalten wir mit (9.145)
erhalten wir mit (9.145)
Wir erhalten also für den Bereich II symmetrische Wellenfunktionen.
Daher nennen wir diesen Fall symmetrisch. Für 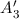 und
und 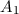 ergibt
sich
ergibt
sich
Die Wellenfunktionen für die drei Bereiche I, II und III nehmen dementsprechend die folgende Form an
Die verbleibende Unbekannte 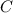 erhalten wir aus der Normierungsbedingung.
Analog zu den Berechnungen beim antisymmetrischen Fall ergibt sich für die
Konstante
erhalten wir aus der Normierungsbedingung.
Analog zu den Berechnungen beim antisymmetrischen Fall ergibt sich für die
Konstante 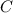
Damit ist die Wellenfunktion für das Teilchen im endlichen Potentialtopf auch im symmetrischen Fall bestimmt. Ebenfalls ergibt sich auf analoge Weise eine transzendente Gleichung zur Bestimmung der Energiewerte
Für die graphische Lösung setzen wir wiederum  und tragen
die Funktionen
und tragen
die Funktionen 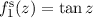 und
und 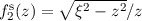 auf (siehe
Abb. 9.7).
auf (siehe
Abb. 9.7).
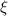 . Die Funktion
. Die Funktion 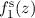 entspricht der schwarzen
durchgezogenen Linie, die Funktion
entspricht der schwarzen
durchgezogenen Linie, die Funktion 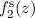 ist durch die rot gepunktete (
ist durch die rot gepunktete (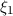 ),
blau gestrichelte (
),
blau gestrichelte (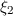 ) und grün durchgezogene Linie (
) und grün durchgezogene Linie (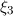 ) dargestellt, wobei
) dargestellt, wobei
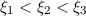 .
.Die erlaubten Werte von  ergeben sich aus den Schnittpunkten dieser
beiden Kurven. Die Anzahl symmetrischer Lösungen
ergeben sich aus den Schnittpunkten dieser
beiden Kurven. Die Anzahl symmetrischer Lösungen 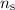 ist gegeben
durch
ist gegeben
durch
wobei  auf die nächsthöhere ganze Zahl rundet. Somit existiert für
auf die nächsthöhere ganze Zahl rundet. Somit existiert für 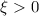 im Gegensatz zum antisymmetrischen Fall auf jeden Fall mindestens eine
Lösung. Die
im Gegensatz zum antisymmetrischen Fall auf jeden Fall mindestens eine
Lösung. Die  entsprechenden Energiewerte
entsprechenden Energiewerte 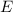 ergeben sich wiederum
aus (9.164).
ergeben sich wiederum
aus (9.164).
Zum Abschluss formulieren wir einige Schlussfolgerungen und zusammenfassende Bemerkungen:
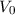 und damit für ein festes
und damit für ein festes 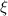
diskrete Zustände, die das Teilchen besetzen kann.  rundet auf die
nächstkleinere ganze Zahl ab. Zum Beispiel ergeben sich für ein Potential mit
rundet auf die
nächstkleinere ganze Zahl ab. Zum Beispiel ergeben sich für ein Potential mit
 : 4 Zustände, 2 antisymmetrische und 2 symmetrische.
: 4 Zustände, 2 antisymmetrische und 2 symmetrische.
 von 0 bis 4 dargestellt.
von 0 bis 4 dargestellt.
 besteht eine
nichtverschwindende Wahrscheinlichkeit das Teilchen ausserhalb des Topfes (in
den Gebieten I und III) anzutreffen.
besteht eine
nichtverschwindende Wahrscheinlichkeit das Teilchen ausserhalb des Topfes (in
den Gebieten I und III) anzutreffen.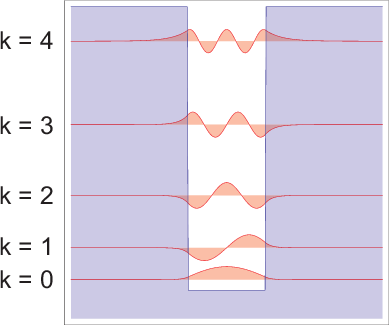
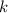 von 0 bis 4.
von 0 bis 4.Wir betrachten ein Teilchen mit kinetischer Energie 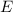 , welches auf eine
Potentialbarriere der Höhe
, welches auf eine
Potentialbarriere der Höhe 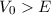 und der Breite
und der Breite 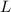 trifft (siehe Abb. 9.9). Nach
den Regeln der klassischen Physik kann das Teilchen die Barriere nicht überwinden.
Quantenmechanisch kann ein Teilchen jedoch eine Potentialbarriere durchdringen
und sich auf der anderen Seite der Barriere weiter fortbewegen. Auf diesen
quantenmechanischen Effekt, den sogenannten Tunneleffekt, gehen wir in diesem
Abschnitt genauer ein.
trifft (siehe Abb. 9.9). Nach
den Regeln der klassischen Physik kann das Teilchen die Barriere nicht überwinden.
Quantenmechanisch kann ein Teilchen jedoch eine Potentialbarriere durchdringen
und sich auf der anderen Seite der Barriere weiter fortbewegen. Auf diesen
quantenmechanischen Effekt, den sogenannten Tunneleffekt, gehen wir in diesem
Abschnitt genauer ein.
 trifft auf eine
Potentialbarriere der Höhe
trifft auf eine
Potentialbarriere der Höhe  und der Breite
und der Breite  .
.Der Tunneleffekt wurde in zahlreichen Experimenten verifiziert, z.B. beim radioaktiven Zerfall oder in elektronischen Tunneldioden. Der Tunneleffekt wird z.B. im Rastertunnelmikroskop (siehe Abschnitt 7.2.3), welches zur Abbildung der Oberfläche verwendet werden kann, auch technisch angewandt. Dessen Funktionsweise beruht darauf, dass es für Elektronen möglich ist die Potentialbarriere zwischen der abtastenden Spitze und der zu untersuchenden Oberfläche einer Probe zu überwinden.
Das Ziel der folgenden Rechnung ist es, die sogenannte Transmissionswahrscheinlichkeit, auch Transmissionskoeffizient genannt, eines Teilchens durch eine Potentialbarriere zu bestimmen. Die Definition lautet folgendermassen:
Definition 9.12 Die Transmissionswahrscheinlichkeit 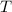 ist definiert als der
transmittierte Teilchenfluss
ist definiert als der
transmittierte Teilchenfluss  geteilt durch den einfallenden Teilchenfluss
geteilt durch den einfallenden Teilchenfluss 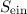 und ist damit ein Mass für die Stärke des Tunneleffekts
und ist damit ein Mass für die Stärke des Tunneleffekts
Der Teilchenfluss 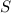 ist dabei gegeben durch
ist dabei gegeben durch
d.h. als Produkt von Wahrscheinlichkeitsdichte 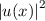 und Teilchengeschwindigkeit
und Teilchengeschwindigkeit
 .
.
Wir beginnen unsere Berechnung, indem wir die x-Achse in drei Bereiche I, II und III unterteilen (siehe Abb. 9.9), für die wir die zeitunabhängige Schrödinger-Gleichung (Potential ist zeitunabhängig) separat lösen
Die Lösung für die drei Bereiche lassen sich analog zu den vorangegangenen
Beispielen mit Hilfe eines Exponentialansatzes bestimmen. Wir verzichten daher auf
eine Herleitung und geben direkt die Lösungen für die Wellenfunktionen 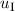 ,
, 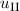 und
und 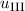 in den drei Bereichen an
in den drei Bereichen an
Es ist zu bemerken, dass im Bereich III aufgrund der betrachteten Situation
(Teilchen kommt von links) nur eine rechtslaufende Welle existieren kann und daher
 ist. Die anderen Koeffizienten
ist. Die anderen Koeffizienten 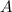 ,
, 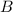 ,
, 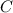 ,
, 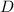 und
und 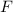 ergeben sich aus den
Stetigkeitsbedingungen bei
ergeben sich aus den
Stetigkeitsbedingungen bei 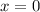 und
und 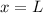 für die Wellenfunktion und deren
Ableitung nach
für die Wellenfunktion und deren
Ableitung nach  . Bevor wir die Koeffizienten
. Bevor wir die Koeffizienten 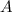 ,
, 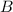 ,
, 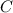 ,
, 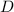 und
und 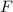 aus diesen Stetigkeitsbedingungen berechnen, gehen wir zurück zu unserem
ursprünglichen Ziel, der Bestimmung der Transmissionswahrscheinlichkeit
aus diesen Stetigkeitsbedingungen berechnen, gehen wir zurück zu unserem
ursprünglichen Ziel, der Bestimmung der Transmissionswahrscheinlichkeit
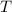 . Mit (9.180) und (9.182) ergibt sich nach Definition 9.12 der folgende
Ausdruck
. Mit (9.180) und (9.182) ergibt sich nach Definition 9.12 der folgende
Ausdruck
wobei 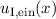 den einfallenden Anteil der Wellenfunktion
den einfallenden Anteil der Wellenfunktion 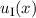 bezeichnet.
Ausserdem haben wir im letzten Schritt verwendet, dass
bezeichnet.
Ausserdem haben wir im letzten Schritt verwendet, dass 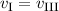 , da sich das
Teilchen in beiden Regionen I und III im potentialfreien Raum bewegt und beim
Tunnelprozess keine kinetische Energie verliert. Demzufolge genügt es das Verhältnis
, da sich das
Teilchen in beiden Regionen I und III im potentialfreien Raum bewegt und beim
Tunnelprozess keine kinetische Energie verliert. Demzufolge genügt es das Verhältnis
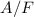 aus den Stetigkeitsbedingungen zu bestimmen. Diese sind gegeben
durch
aus den Stetigkeitsbedingungen zu bestimmen. Diese sind gegeben
durch
In Matrixschreibweise lautet dieses Gleichungssystem
Elementare Zeilenumformungen für lineare Gleichungssysteme liefern
Wir drücken nun mit (9.189) Schritt für Schritt die Koeffizienten 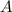 ,
, 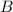 ,
, 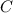 und
und
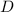 durch den Koeffizient
durch den Koeffizient 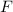 aus, um dann schliesslich zum Verhältnis
aus, um dann schliesslich zum Verhältnis 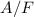 zu
gelangen. Für den Koeffizient
zu
gelangen. Für den Koeffizient 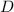 ergibt sich
ergibt sich
Damit erhalten wir für den Koeffizient 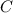
Für den Koeffizient 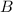 resultiert
resultiert
Schlussendlich erhalten wir daraus für das Verhältnis 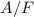
Wir vereinfachen diesen Ausdruck, indem wir folgende zwei Annahmen tätigen:
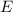 sei klein gegenüber der Höhe der Potentialbarriere
sei klein gegenüber der Höhe der Potentialbarriere 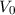 ,
d.h.
,
d.h. 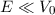 . Damit ergibt sich:
. Damit ergibt sich: 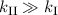 und daraus
und daraus 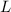 sei
sei 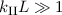 , d.h. wir betrachten breite Barrieren.
Daraus folgt
, d.h. wir betrachten breite Barrieren.
Daraus folgt Mit diesen beiden Annahmen (9.194) und (9.195) vereinfacht sich der Ausdruck (9.193)
für das Verhältnis 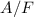 folgendermassen
folgendermassen
Einsetzen in (9.183) liefert für die Transmissionswahrscheinlichkeit
Mit den Ausdrücken 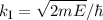 und
und 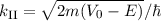 ergibt sich das
folgende Schlussresultat
ergibt sich das
folgende Schlussresultat
D.h. die Transmissionswahrscheinlichkeit zeigt eine starke exponentielle
Ab-hängigkeit von Teilchenenergie 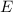 und der Breite der Barriere
und der Breite der Barriere 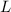 .
.
Um nun eine Vorstellung über die Stärke des Tunneleffekts zu erhalten, betrachten
wir das folgende Beispiel: Ein Elektron mit kinetischer Energie 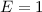 eV bewegt
sich auf eine Potentialbarriere der Höhe
eV bewegt
sich auf eine Potentialbarriere der Höhe 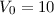 eV und Breite
eV und Breite 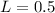 nm zu.
Wie gross ist die Transmissionswahrscheinlichkeit
nm zu.
Wie gross ist die Transmissionswahrscheinlichkeit 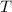 , d.h. die Wahrscheinlichkeit,
dass das Elektron die Barriere überwinden kann? Einsetzen der Werte in (9.198)
liefert das folgende Ergebnis
, d.h. die Wahrscheinlichkeit,
dass das Elektron die Barriere überwinden kann? Einsetzen der Werte in (9.198)
liefert das folgende Ergebnis
Das bedeutet, dass selbst für leichte Teilchen und niedrige Barrieren die
Transmissionswahrscheinlichkeit 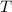 sehr klein ist. Dennoch ist der Tunneleffekt experimentell
beobachtbar und findet, wie bereits zu Beginn des Abschnitts erwähnt, zum Beispiel beim
Rastertunnelmikroskop5
(siehe Abschnitt 7.2.3) seine Anwendung.
sehr klein ist. Dennoch ist der Tunneleffekt experimentell
beobachtbar und findet, wie bereits zu Beginn des Abschnitts erwähnt, zum Beispiel beim
Rastertunnelmikroskop5
(siehe Abschnitt 7.2.3) seine Anwendung.
Zum Abschluss dieses Abschnitts geben wir das Resultat einer Mathematica Berechnung
für die Wellenfunktion (Realteil) und die entsprechende Wahrscheinlichkeitsdichte für
die Zahlenwerte 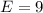 eV,
eV,  eV und
eV und  nm wider (siehe
Abb. 9.10). Aus dieser graphischen Darstellung wird ersichtlich, dass die
Wellenfunktion vor und nach der Potentialbarriere oszilliert und innerhalb der
Barriere exponentiell abfällt. Die Wahrscheinlichkeitsdichte oszilliert ebenfalls
vor der Potentialbarriere, da sich dort eine stehende Welle aus einfallender
und reflektierter Materiewelle ausbildet. Innerhalb der Barriere fällt die
Wahrscheinlichkeitsdichte exponentiell ab und hat nach der Barriere einen konstanten
Wert, da sich das Teilchen dort als ebene Welle nur nach rechts ausbreitet.
nm wider (siehe
Abb. 9.10). Aus dieser graphischen Darstellung wird ersichtlich, dass die
Wellenfunktion vor und nach der Potentialbarriere oszilliert und innerhalb der
Barriere exponentiell abfällt. Die Wahrscheinlichkeitsdichte oszilliert ebenfalls
vor der Potentialbarriere, da sich dort eine stehende Welle aus einfallender
und reflektierter Materiewelle ausbildet. Innerhalb der Barriere fällt die
Wahrscheinlichkeitsdichte exponentiell ab und hat nach der Barriere einen konstanten
Wert, da sich das Teilchen dort als ebene Welle nur nach rechts ausbreitet.
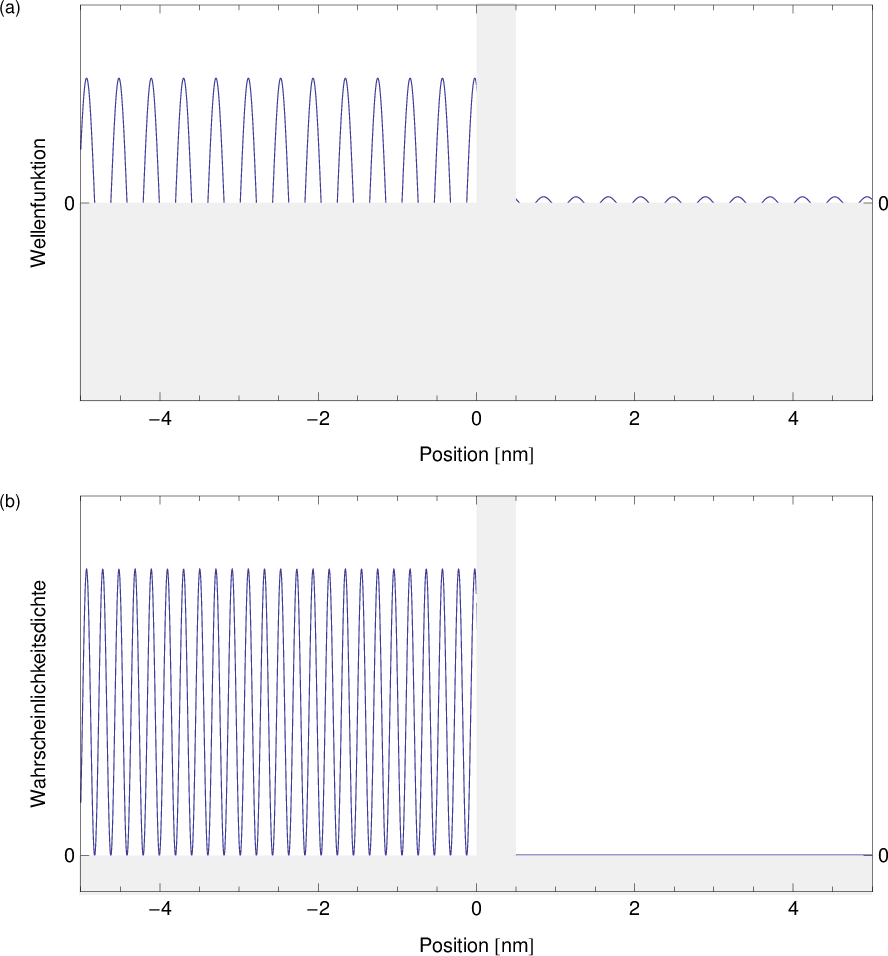
![Re [u (x )]](PhysikIV2629x.png) und
(b) Wahrscheinlichkeitsdichte
und
(b) Wahrscheinlichkeitsdichte  für ein Elektron, das sich mit einer
kinetischen Energie
für ein Elektron, das sich mit einer
kinetischen Energie 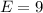 eV auf eine Potentialbarriere der Höhe
eV auf eine Potentialbarriere der Höhe 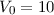 eV
und Breite
eV
und Breite 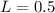 nm zubewegt und diese „tunnelt“.
nm zubewegt und diese „tunnelt“.Wie bereits zuvor diskutiert ergibt sich ein Wellenpaket als Superposition von vielen
harmonischen Wellen mit verschiedenen Frequenzen  und Wellenzahlen
und Wellenzahlen 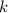 (siehe
Abschnitt 6.4). Die verschiedenen Frequenzen
(siehe
Abschnitt 6.4). Die verschiedenen Frequenzen 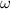 entsprechen verschiedenen
Energien
entsprechen verschiedenen
Energien 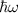 .
.
Wir betrachten hier die Bewegung eines Gaussschen Wellenpakets durch
einen Potentialtopf der Tiefe 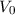 und durch eine Potentialbarriere der Höhe
und durch eine Potentialbarriere der Höhe
 hindurch. Dieses Problem lässt sich durch Lösung der zeitabhängigen
Schröd-inger-Gleichung (9.94) bearbeiten. Die Berechnung eines solchen Problems
lässt sich nur schwierig von Hand bewältigen. Wir geben hier das Resultat einer
Computerberechnung wieder, welche von Abraham Goldberg und seinen
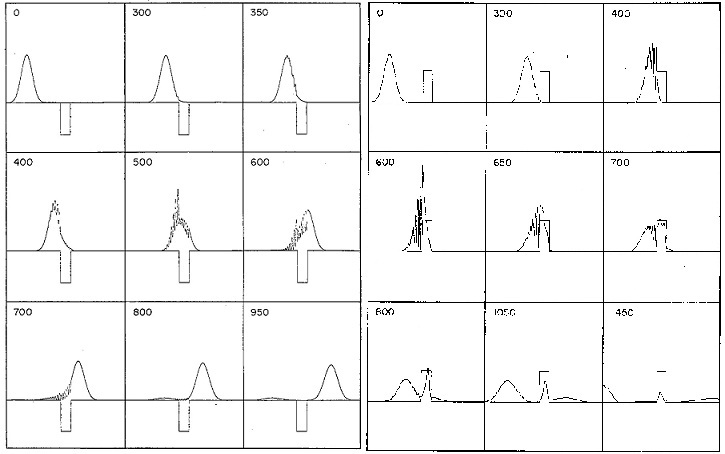
Mitarbeitern im Jahr 1967 [12] durchgeführt wurde. Diese zeigen, dass sich das
Wellenpaket am Potentialtopf und an der Barriere, für den Fall dass die
Teilchenenergie sehr viel grösser ist als die Topftiefe oder die Barrierenhöhe
hindurch. Dieses Problem lässt sich durch Lösung der zeitabhängigen
Schröd-inger-Gleichung (9.94) bearbeiten. Die Berechnung eines solchen Problems
lässt sich nur schwierig von Hand bewältigen. Wir geben hier das Resultat einer
Computerberechnung wieder, welche von Abraham Goldberg und seinen
Mitarbeitern im Jahr 1967 [12] durchgeführt wurde. Diese zeigen, dass sich das
Wellenpaket am Potentialtopf und an der Barriere, für den Fall dass die
Teilchenenergie sehr viel grösser ist als die Topftiefe oder die Barrierenhöhe
 , im Wesentlichen wie ein klassisches Teilchen verhält. Das Teilchen
überwindet die durch die Barriere oder den Topf dargestellte Störung mit hoher
Wahrscheinlichkeit und wird nur mit einer niedrigen Wahrscheinlichkeit
reflektiert. Für
, im Wesentlichen wie ein klassisches Teilchen verhält. Das Teilchen
überwindet die durch die Barriere oder den Topf dargestellte Störung mit hoher
Wahrscheinlichkeit und wird nur mit einer niedrigen Wahrscheinlichkeit
reflektiert. Für  wird das Teilchen sowohl vom Topf als auch von der
Barriere reflektiert. Für die Barriere entspricht dies angenähert ebenfalls den
klassischen Vorstellungen. Drastische Abweichung vom klassischen Verhalten
kommen jedoch zum Vorschein, wenn die Teilchenenergie von ähnlicher Grösse
ist wie die Barrierenhöhe oder die Topftiefe (siehe Abb. 9.11). Vergleiche
dazu die Ausführungen zum Tunneleffekt im vorangegangenen Abschnitt.
wird das Teilchen sowohl vom Topf als auch von der
Barriere reflektiert. Für die Barriere entspricht dies angenähert ebenfalls den
klassischen Vorstellungen. Drastische Abweichung vom klassischen Verhalten
kommen jedoch zum Vorschein, wenn die Teilchenenergie von ähnlicher Grösse
ist wie die Barrierenhöhe oder die Topftiefe (siehe Abb. 9.11). Vergleiche
dazu die Ausführungen zum Tunneleffekt im vorangegangenen Abschnitt.
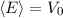 . [12]
. [12]
Wir illustrieren zunächst die Bedeutung von scharfen bzw. unscharfen Observablen anhand von einigen Beispielen und geben anschliessend die genaue mathematische Definition. Bei den Beispielen beziehen wir uns auf die Heisenbergsche Unschärferelation (siehe Abschnitt 9.2).
Bei der Bewegung eines Teilchens (Massepunkt) in einem zeitunabhängigen Potential
bleibt die Gesamtenergie 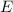 konstant. Zur Messung der Energie steht damit
eine beliebig lange Zeitspanne
konstant. Zur Messung der Energie steht damit
eine beliebig lange Zeitspanne 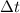 zur Verfügung. Da
zur Verfügung. Da 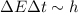 , also
endlich ist, kann die Unschärfe
, also
endlich ist, kann die Unschärfe 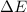 einer Messung der Energie beliebig
klein werden. Man sagt in diesem Fall: Die Energie hat den scharfen Wert
einer Messung der Energie beliebig
klein werden. Man sagt in diesem Fall: Die Energie hat den scharfen Wert
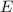 .
.
Zum Beispiel haben wir beim Teilchen im Potentialtopf gesehen (siehe
Abschnitte 9.1.1 und 9.4.2), dass die Energie verschiedene scharfe und diskrete
Werte 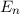 annehmen kann, welche durch die Quantenzahl
annehmen kann, welche durch die Quantenzahl 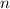 charakterisiert
sind.
charakterisiert
sind.
Bei genauerer Betrachtung findet man jedoch, dass die Schärfe der Differenz zweier Energien eines quantenmechanischen Systems immer durch die Lebensdauer der mit dem Übergang verknüpften Zustände begrenzt ist. Diese Zustände können, wie wir bereits kennengelernt haben, im Prozess der spontanen Emission, hervorgerufen durch die Wechselwirkung mit den Vakuumfluktuationen des elektromagnetischen Feldes, auf einer durch die Einstein-Koeffizienten bestimmten Zeitskala zerfallen.
Nach Abschnitt 9.4.2 ist die Lösung der Schrödinger-Gleichung für ein Teilchen im räumlich und zeitlich konstanten Potential eine ebene, harmonische Welle
Da der Zustand stationär ist, ist die Energie scharf. Im Gegensatz zum Teilchen im Potentialtopf sind die Werte, die sie annehmen kann, jedoch beliebig und nicht diskret.
Die Wahrscheinlichkeitsdichte 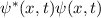 ist räumlich (und zeitlich) konstant.
D.h. der genaue Aufenthaltsort des Teilchens ist unbestimmt oder mit anderen
Worten, die Unschärfe
ist räumlich (und zeitlich) konstant.
D.h. der genaue Aufenthaltsort des Teilchens ist unbestimmt oder mit anderen
Worten, die Unschärfe 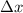 des Ortes ist unendlich. Da
des Ortes ist unendlich. Da 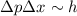 endlich ist,
verschwindet die Unschärfe
endlich ist,
verschwindet die Unschärfe 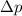 des Impulses
des Impulses 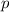 . D.h. neben der Energie
. D.h. neben der Energie 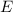 nimmt
auch der Impuls
nimmt
auch der Impuls 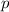 einen scharfen Wert an. Auch beim Impuls sind die Werte
beliebig und nicht diskret.
einen scharfen Wert an. Auch beim Impuls sind die Werte
beliebig und nicht diskret.
Im Gegensatz zu diesen Beispielen haben wir bei der Beugung am Spalt (siehe
Abschnitt 9.2.1) und beim Gaussschen Wellenpaket (siehe Abschnitt 9.2.2) gesehen,
dass sowohl der Ort  als auch der Impuls
als auch der Impuls 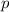 unscharfe Werte annehmen. Dabei
sind die Unschärfen
unscharfe Werte annehmen. Dabei
sind die Unschärfen 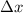 und
und 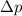 von Ort und Impuls durch die Heisenbergsche
Unschärferelation miteinander verknüpft.
von Ort und Impuls durch die Heisenbergsche
Unschärferelation miteinander verknüpft.
Diesen Beispielen folgend geben wir nun eine mathematische Definition an, unter
welchen Bedingungen der Erwartungswert 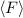 einer Observablen
einer Observablen 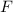 scharf
bestimmt ist.
scharf
bestimmt ist.
Definition 9.13 Für ein Teilchen im Zustand 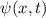 ist der Erwartungswert
ist der Erwartungswert
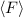 einer Observablen
einer Observablen 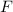 scharf bestimmt, wenn bei wiederholter Messung an
identisch gleich präparierten Teilchen immer der selbe Wert
scharf bestimmt, wenn bei wiederholter Messung an
identisch gleich präparierten Teilchen immer der selbe Wert 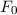 resultiert.
Mathematisch bedeutet das, dass die Unschärfe
resultiert.
Mathematisch bedeutet das, dass die Unschärfe 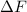 verschwinden muss
verschwinden muss
Der Index 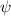 soll daran erinnern, dass diese Beziehung für ein Teilchen im Zustand
soll daran erinnern, dass diese Beziehung für ein Teilchen im Zustand
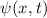 gilt, denn es hängt vom Zustand ab, ob der Erwartungswert einer Observable
einen scharfen Wert annimmt oder nicht.
gilt, denn es hängt vom Zustand ab, ob der Erwartungswert einer Observable
einen scharfen Wert annimmt oder nicht.
Wir werden nun zeigen, dass sich mit Hilfe des Operatorformalismusses eine einfache
Bedingung angeben lässt, die erfüllt sein muss, damit der Erwartungswert  einer Observable
einer Observable  im Zustand
im Zustand 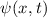 einen scharfen Wert besitzt. Wir
betrachten diese Observable als Funktion
einen scharfen Wert besitzt. Wir
betrachten diese Observable als Funktion 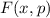 oder allgemeiner als Funktion
oder allgemeiner als Funktion
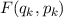 der verallgemeinerten Koordinaten
der verallgemeinerten Koordinaten 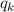 und der dazu kanonisch
konjugierten Impulse
und der dazu kanonisch
konjugierten Impulse 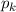 . Wir betrachten hier stationäre (zeitunabhängige)
Zustände und interpretieren die Bildung der Erwartungswerte als Mittelung vieler
Messungen an identischen, gleich präparierten Teilchen.
. Wir betrachten hier stationäre (zeitunabhängige)
Zustände und interpretieren die Bildung der Erwartungswerte als Mittelung vieler
Messungen an identischen, gleich präparierten Teilchen.
Satz 9.1 Sei der Zustand jedes betrachteten Teilchens beschrieben durch die
Wellenfunktion 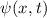 im Ortsraum, dann gilt: Der Erwartungswert
im Ortsraum, dann gilt: Der Erwartungswert 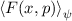 einer Observable
einer Observable 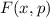 nimmt genau dann den scharfen Wert
nimmt genau dann den scharfen Wert  an, wenn die
Wellenfunktion
an, wenn die
Wellenfunktion 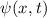 die folgende Gleichung erfüllt
die folgende Gleichung erfüllt
Die Gleichung (9.202) wird als Eigenwertgleichung bezeichnet. Sie besagt, dass
sich die Wellenfunktion 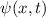 bis auf den Faktor
bis auf den Faktor  reproduziert, wenn man den
Operator
reproduziert, wenn man den
Operator  auf sie anwendet. Eine Wellenfunktion
auf sie anwendet. Eine Wellenfunktion 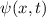 , die (9.202) erfüllt, ist
eine Eigenfunktion des Operators
, die (9.202) erfüllt, ist
eine Eigenfunktion des Operators 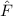 . Der scharfe Wert
. Der scharfe Wert 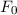 , den der
Erwartungswert
, den der
Erwartungswert 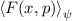 annimmt, wird Eigenwert des Operators
annimmt, wird Eigenwert des Operators 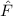 genannt.
genannt.
In der Impulsraumdarstellung gilt ein entsprechender Satz für die Wellenfunktion
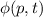 . Es ist zu beachten, dass der Operator
. Es ist zu beachten, dass der Operator 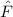 in dieser Darstellung eine andere
Form besitzt als in der Ortsraumdarstellung.
in dieser Darstellung eine andere
Form besitzt als in der Ortsraumdarstellung.
Beweis des Satzes:
Nach Definition 9.13 für den scharfen Wert des Erwartungswerts 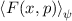 einer
Observable
einer
Observable 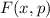 ist folgende Äquivalenz zu zeigen
ist folgende Äquivalenz zu zeigen
wobei 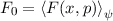 . Wir betrachten die beiden Richtungen einzeln.
. Wir betrachten die beiden Richtungen einzeln.
„ “
“
Mit Hilfe der Eigenwertgleichung (9.202) folgt für den Erwartungswert
Für den Erwartungswert 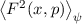 von
von 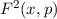 ergibt sich
ergibt sich
Somit erhalten wir für die Unschärfe 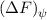 von
von 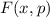
„ “
“
Aus 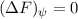 folgt mit der Eigenschaft, dass in der Quantenmechanik die
Operatoren hermitesch sind
folgt mit der Eigenschaft, dass in der Quantenmechanik die
Operatoren hermitesch sind
Dieses Integral verschwindet nur dann, wenn gilt
d.h. wenn folgende Gleichung erfüllt ist

Wir fassen diesen Abschnitt zusammen:
Genau dann wenn bei wiederholter Messung der Observablen 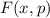 an
identischen, im selben Zustand
an
identischen, im selben Zustand 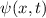 präparierten Teilchen, immer der selbe Wert
präparierten Teilchen, immer der selbe Wert
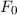 gemessen wird, ist
gemessen wird, ist 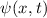 eine Eigenfunktion des Operators
eine Eigenfunktion des Operators 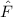 zum Eigenwert
zum Eigenwert
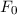 . Man sagt dann, das Teilchen befindet sich in einem Eigenzustand des Operators
. Man sagt dann, das Teilchen befindet sich in einem Eigenzustand des Operators
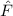 der zum Eigenwert
der zum Eigenwert 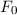 gehört.
gehört.
Wir betrachten hier verschiedene Operatoren, die wir in Abschnitt 9.3.2 kennengelernt haben und bestimmen ihre Eigenfunktionen und Eigenwerte.
Wir betrachten ein Teilchen, das sich in einem zeitunabhängigen Potential
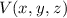 bewegt. Seine Gesamtenergie
bewegt. Seine Gesamtenergie 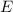 ist dann konstant und damit scharf
messbar, wenn sich das Teilchen in einem Eigenzustand des Operators befindet. Nach
Abschnitt 9.5.1 ist somit
ist dann konstant und damit scharf
messbar, wenn sich das Teilchen in einem Eigenzustand des Operators befindet. Nach
Abschnitt 9.5.1 ist somit 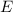 ein Eigenwert des Hamilton-Operators
ein Eigenwert des Hamilton-Operators 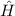 . Die
Eigenwertgleichung lautet
. Die
Eigenwertgleichung lautet
Andererseits gilt die Schrödinger-Gleichung
Aus (9.210) und (9.211) folgt die Gleichung
mit der allgemeinen Lösung
Andererseits kann die zeitunabhängige Schrödinger-Gleichung (9.109) als Eigenwertgleichung aufgefasst werden, indem wir schreiben
Wir halten fest
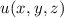 Eigenfunktionen des
Hamilton-Operators.
Eigenfunktionen des
Hamilton-Operators.Das Teilchen im Potentialtopf (siehe Abschnitte 9.1.1 und 9.4.2) ist ein
instruktives Beispiel für das Auftreten diskreter Energiewerte 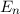 . Zu jedem
Eigenwert
. Zu jedem
Eigenwert 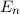 des Hamilton-Operators gehört eine Eigenfunktion
des Hamilton-Operators gehört eine Eigenfunktion 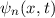 bzw.
bzw.
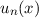 .
.
Wir betrachten einfachheitshalber ein eindimensionales System. Die Eigenwertgleichung lautet
mit der allgemeinen Lösung
wobei 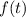 als Amplitude aufzufassen ist. Diese Funktion ist räumlich periodisch
und stellt ein Teilchen dar, das einen scharf bestimmten Impuls
als Amplitude aufzufassen ist. Diese Funktion ist räumlich periodisch
und stellt ein Teilchen dar, das einen scharf bestimmten Impuls 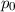 hat, dessen
Position aber völlig unbestimmt ist. Damit ist die Unschärfe des Ortes unendlich
gross. Dies ist im Einklang mit der Heisenbergschen Unschärferelation (9.37).
hat, dessen
Position aber völlig unbestimmt ist. Damit ist die Unschärfe des Ortes unendlich
gross. Dies ist im Einklang mit der Heisenbergschen Unschärferelation (9.37).
Wir beschränken uns wiederum auf eine Dimension und betrachten zusätzlich ein zeitunabhängiges Problem. Die Eigenwertgleichung nimmt dann folgende Form an
Der Ortsoperator in der Ortsraumdarstellung entspricht dem Faktor  . Demzufolge
können wir schreiben
. Demzufolge
können wir schreiben
Nach dieser Gleichung muss 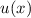 verschwinden für alle
verschwinden für alle 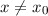 . Bei
. Bei 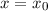 ist
ist
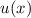 unendlich und zwar so, dass
unendlich und zwar so, dass
D.h. 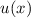 entspricht einer sogenannten Diracschen Deltafunktion
entspricht einer sogenannten Diracschen Deltafunktion
Eine solche Deltafunktion kann man angenähert als beliebig schmales Gausssches Wellenpaket beschreiben
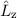
Der Zustand eines Teilchens im dreidimensionalen Raum sei in Kugelkoordinaten
ausgedrückt 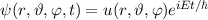 . Wir betrachten hier wiederum ein
zeitunabhängiges Problem. Somit lautet die Eigenwertgleichung für den Operator
. Wir betrachten hier wiederum ein
zeitunabhängiges Problem. Somit lautet die Eigenwertgleichung für den Operator
Mit (9.68) ergibt sich
Die allgemeine Lösung dieser Gleichung ist
Das erste Postulat (siehe Abschnitt 9.1) verlangt, dass die Wellenfunktion eindeutig
sein muss. Daraus ergibt sich für die Wellenfunktion  folgende notwendige
Bedingung
folgende notwendige
Bedingung
D.h. es muss gelten
Diese Gleichung ist erfüllt, wenn
Damit ergibt sich
Die Eigenwerte  des Operators
des Operators 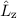 sind ganzzahlige Vielfache von
sind ganzzahlige Vielfache von
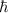
Zu jedem Eigenwert (zu jeder Quantenzahl) 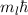 gehört eine Eigenfunktion
gehört eine Eigenfunktion
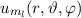
Aus diesen Betrachtungen ergibt sich, dass die z-Komponente des Bahndrehimpulses
- wenn sie einen scharfen Wert besitzt - nur die diskreten Werte 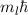 annehmen
kann. Dies gilt nur für eine ausgezeichnete Richtung des Raumes, in diesem Fall die
z-Richtung. Entlang der beiden dazu orthogonalen Raumrichtungen,
annehmen
kann. Dies gilt nur für eine ausgezeichnete Richtung des Raumes, in diesem Fall die
z-Richtung. Entlang der beiden dazu orthogonalen Raumrichtungen,  und
und  , ist
der Bahndrehimpuls unscharf. Diese Tatsache werden wir in einem späteren Kapitel
noch genauer diskutieren.
, ist
der Bahndrehimpuls unscharf. Diese Tatsache werden wir in einem späteren Kapitel
noch genauer diskutieren.
Das dritte Postulat der Quantenmechanik lautet:
Postulat 3 Das Ergebnis einer einzelnen Messung einer Observablen  ist
ein Eigenwert des zugehörigen Operators
ist
ein Eigenwert des zugehörigen Operators  . Erhält man bei einer Messung den
Eigenwert
. Erhält man bei einer Messung den
Eigenwert 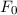 , so geht die Wellenfunktion in die entsprechende Eigenfunktion
, so geht die Wellenfunktion in die entsprechende Eigenfunktion
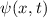 über. D.h. befindet sich das System vor der Messung einer Observablen
über. D.h. befindet sich das System vor der Messung einer Observablen
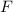 nicht in einem Eigenzustand des entsprechenden Operators
nicht in einem Eigenzustand des entsprechenden Operators 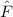 , so ändert
die Messung den Zustand des System, sodass sich das System nach der Messung
in einem Eigenzustand des Operators
, so ändert
die Messung den Zustand des System, sodass sich das System nach der Messung
in einem Eigenzustand des Operators 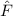 befindet. Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der Observablen
befindet. Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der Observablen
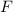 einem Eigenzustand des entsprechenden Operators
einem Eigenzustand des entsprechenden Operators 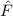 entspricht.
entspricht.
Wir illustrieren Postulat 3 am Beispiel des Bahndrehimpulses aus dem vorangegangenen Abschnitt. Wir betrachten die Messung der Komponente des Bahndrehimpulses eines Teilchens längs einer vorgegebenen Achse. Eine solche ausgezeichnete Achse kann zum Beispiel durch die Richtung eines angelegten homogenen Magnetfeldes vorgegeben sein, eine Situation die wir im Kontext des Zeeman-Effekts noch genauer diskutieren werden. Es ist in der Quantenmechanik üblich, diese Achse, längs der die Komponente des Bahndrehimpulses gemessen wird, als z-Achse zu bezeichnen.
Als Ergebnis einer solchen Messung der z-Komponente des Bahndrehimpulses
 ergeben sich nach Postulat 3 und Abschnitt 9.5.2 nur die diskreten
Werte
ergeben sich nach Postulat 3 und Abschnitt 9.5.2 nur die diskreten
Werte 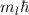 , d.h. die Eigenwerte des entsprechenden Operators
, d.h. die Eigenwerte des entsprechenden Operators 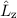 . Führt
man diese Messung nun an gleich präparierten Teilchen durch und misst
jedes Mal den selben Wert (Eigenwert)
. Führt
man diese Messung nun an gleich präparierten Teilchen durch und misst
jedes Mal den selben Wert (Eigenwert) 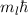 , dann war der Zustand der
Teilchen vor der Messung ein Eigenzustand von
, dann war der Zustand der
Teilchen vor der Messung ein Eigenzustand von 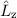 und der Zustand der
Teilchen wird durch die Messung nicht verändert. Misst man hingegen an
gleich präparierten Teilchen verschiedene Werte (Eigenwerte)
und der Zustand der
Teilchen wird durch die Messung nicht verändert. Misst man hingegen an
gleich präparierten Teilchen verschiedene Werte (Eigenwerte) 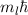 , dann
war der Zustand der Teilchen vor der Messung kein Eigenzustand von
, dann
war der Zustand der Teilchen vor der Messung kein Eigenzustand von 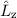 .
Nach der Messung befinden sich in diesem Fall die Teilchen in verschiedenen
Eigenzuständen von
.
Nach der Messung befinden sich in diesem Fall die Teilchen in verschiedenen
Eigenzuständen von 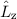 zu den entsprechenden Eigenwerten (Messresultaten)
zu den entsprechenden Eigenwerten (Messresultaten)
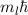 .
.
Nach Satz 9.1 nimmt der Erwartungswert 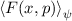 einer Observable
einer Observable 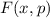 den scharfen Wert
den scharfen Wert  an, wenn der Zustand des Teilchens
an, wenn der Zustand des Teilchens 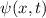 die
Eigenwertgleichung
die
Eigenwertgleichung
erfüllt. Es stellt sich nun die Frage, ob Zustände 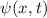 existieren, für die die
Erwartungswerte von zwei Observablen gleichzeitig scharf sind. Diese Frage ist mit
„ja“ zu beantworten, wie das folgende Beispiel zeigt.
existieren, für die die
Erwartungswerte von zwei Observablen gleichzeitig scharf sind. Diese Frage ist mit
„ja“ zu beantworten, wie das folgende Beispiel zeigt.
Die Wellenfunktion
stellt ein Teilchen dar, das sich im zeitlich und räumlich konstanten Potential längs
der x-Achse bewegt. Nach Abschnitt 9.5.1 sind die Energie 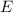 und auch der Impuls
und auch der Impuls
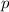 gleichzeitig scharf. Dies lässt sich nochmals verdeutlichen, indem wir die
Wellenfunktion
gleichzeitig scharf. Dies lässt sich nochmals verdeutlichen, indem wir die
Wellenfunktion 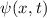 als Produkt schreiben
als Produkt schreiben
Daraus wird ersichtlich, dass es sich um eine simultane Eigenfunktion der Operatoren
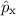 und
und 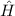 handelt. Denn eine Eigenfunktion von
handelt. Denn eine Eigenfunktion von 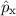 hat nach (9.216) die
allgemeine Form
hat nach (9.216) die
allgemeine Form
und eine Eigenfunktion von 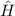 hat nach (9.213) die allgemeine Form
hat nach (9.213) die allgemeine Form
Das Ziel ist es nun ein allgemeines Kriterium zu formulieren, welches angibt, ob zwei Observable gleichzeitig scharf messbar sind. Im Zusammenhang mit der Erklärung der Bedeutung des Kommutators (siehe Abschnitt 9.3.3) haben wir diese Frage schon einmal gestreift, indem wir gesagt haben, dass die Erwartungswerte nicht kommutierender Operatoren gleichzeitig nicht mit beliebiger Genauigkeit bestimmt werden können. Wie angekündigt wollen wir nun diese Aussage präziser formulieren und beweisen. Es gilt der folgende Satz:
Satz 9.2 Die Erwartungswerte von zwei Observablen 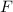 und
und 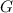 eines Teilchens
im Zustand
eines Teilchens
im Zustand 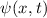 sind dann und nur dann gleichzeitig scharf, wenn die
Anwendung des Kommutators der entsprechenden Operatoren
sind dann und nur dann gleichzeitig scharf, wenn die
Anwendung des Kommutators der entsprechenden Operatoren 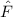 und
und 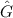 auf die
Wellenfunktion
auf die
Wellenfunktion 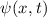 null ergibt
null ergibt
Beweis:
Wir betrachten die beiden Richtungen einzeln.
„ “
“
Wenn 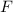 und
und 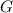 gleichzeitig scharf sind, dann gelten nach Satz 9.1 die
Eigenwertgleichungen
gleichzeitig scharf sind, dann gelten nach Satz 9.1 die
Eigenwertgleichungen
Damit ergibt sich
„ “
“
Zu zeigen ist, dass wenn die Anwendung des Kommutators ![[Fˆ, ˆG]](PhysikIV2821x.png) auf die
Wellenfunktion
auf die
Wellenfunktion 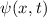 null ergibt,
null ergibt,  eine Eigenfunktion von
eine Eigenfunktion von  und
und  ist.6
ist.6
Es sei (ohne Beschränkung der Allgemeinheit) 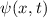 eine Eigenfunktion von
eine Eigenfunktion von 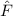 ,
dann gilt
,
dann gilt
Da ![[Fˆ, ˆG]ψ(x,t) = 0](PhysikIV2829x.png) gilt
gilt
Mit (9.239) erhalten wir
Da 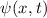 die einzige Eigenfunktion von
die einzige Eigenfunktion von 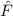 zum Eigenwert
zum Eigenwert 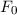 ist, muss
ist, muss 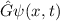 proportional zu
proportional zu 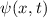 sein. Wir bezeichnen die Proportionalitätskonstante mit
sein. Wir bezeichnen die Proportionalitätskonstante mit
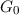 und erhalten
und erhalten
d.h. 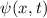 ist gleichzeitig auch eine Eigenfunktion von
ist gleichzeitig auch eine Eigenfunktion von 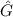 . Für den Beweis des
entarteten Falls verweisen wir auf weiterführende Literatur [11].
. Für den Beweis des
entarteten Falls verweisen wir auf weiterführende Literatur [11].

 und
und  für jede beliebige
Wellenfunktion
für jede beliebige
Wellenfunktion 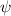 nicht. Demzufolge gibt es nach Satz 9.2 keinen
Zustand, bei dem
nicht. Demzufolge gibt es nach Satz 9.2 keinen
Zustand, bei dem  und
und 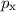 gleichzeitig scharf sind. Dies ist in
Übereinstimmung mit der Unschärferelation (9.37).
gleichzeitig scharf sind. Dies ist in
Übereinstimmung mit der Unschärferelation (9.37).
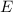 , das Quadrat des Bahndrehimpulsvektors
, das Quadrat des Bahndrehimpulsvektors 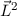 und die
z-Komponente
und die
z-Komponente 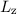 des Bahndrehimpulses. Entsprechend gilt nach Satz 9.2
des Bahndrehimpulses. Entsprechend gilt nach Satz 9.2
Die allgemeine mathematische Definition für die Orthogonalität zweier Funktionen lautet:
Zum Beispiel sind die Funktionen 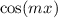 und
und 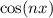 bei ganzzahligen
bei ganzzahligen 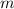 und
und 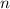 im Variablenbereich
im Variablenbereich 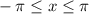 orthogonal für
orthogonal für  , denn es
gilt
, denn es
gilt
Die gleiche Orthogonalitätsbedingung erfüllen auch die Funktionen 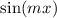 und
und 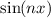 . Es sind genau diese Orthogonalitätseigenschaften, die die
Fourier-Entwicklung ermöglichen.
. Es sind genau diese Orthogonalitätseigenschaften, die die
Fourier-Entwicklung ermöglichen.
Für die Wellenfunktionen 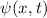 gilt der folgende Satz:
gilt der folgende Satz:
Satz 9.3 Es seien 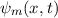 und
und 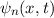 Eigenfunktionen des hermiteschen
Operators
Eigenfunktionen des hermiteschen
Operators 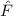 , die zu verschiedenen Eigenwerten
, die zu verschiedenen Eigenwerten 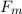 und
und 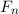 gehören. Dann sind
gehören. Dann sind
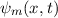 und
und 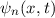 orthogonal in ihrem räumlichen Existenzgebiet,
d.h.
orthogonal in ihrem räumlichen Existenzgebiet,
d.h.
Beweis:
 erfüllen die Bedingung (9.91)
erfüllen die Bedingung (9.91) Wir beweisen nun in einem ersten Schritt, dass dann auch gilt
Es sei 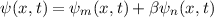 , wobei
, wobei  beliebig. Für diese
Wellenfunktion gilt nach (9.247)
beliebig. Für diese
Wellenfunktion gilt nach (9.247)
Ausmultiplizieren liefert
Indem wir wiederum die Bedingung (9.247) für hermitesche Operatoren ausnützen, lassen sich einige Terme wegkürzen und wir erhalten
Mit den Bezeichnungen 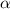 und
und 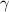 können wir (9.251) schreiben
können wir (9.251) schreiben
Für 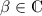 dürfen wir einen beliebigen Wert annehmen. Wir wählen einmal
dürfen wir einen beliebigen Wert annehmen. Wir wählen einmal
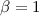 und einmal
und einmal 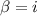 und erhalten damit die Gleichungen
und erhalten damit die Gleichungen 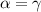 und
und
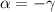 mit der Lösung
mit der Lösung 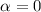 und
und 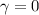 , d.h.
, d.h.
Jede dieser Gleichungen ist äquivalent zu (9.248), womit die Richtigkeit von (9.248) bewiesen ist.
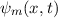 und
und 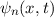 von
von 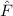 , die zu
den (reellen) Eigenwerten
, die zu
den (reellen) Eigenwerten 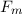 und
und 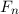 gehören. Die entsprechenden
Eigenwertgleichungen lauten dann
gehören. Die entsprechenden
Eigenwertgleichungen lauten dann Einsetzen in (9.248) liefert
d.h. für  gilt
gilt

Wir illustrieren Satz 9.3 an zwei bekannten Beispielen:
Die Orthogonalität der Eigenfunktionen des Hamilton-Operators für ein
Teilchen im (unendlichen) Potentialtopf ist für  und
und 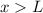 offensichtlich. Wir zeigen nun, dass die Orthogonalitätsbedingung auch für
offensichtlich. Wir zeigen nun, dass die Orthogonalitätsbedingung auch für
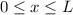 erfüllt ist. Nach Abschnitt 9.4.2 nehmen die Eigenfunktionen
folgende Form an
erfüllt ist. Nach Abschnitt 9.4.2 nehmen die Eigenfunktionen
folgende Form an
Damit ergibt sich
Das Integral über die ersten beiden Summanden verschwindet. Für das Integral über die letzten beiden Summanden müssen wir eine Fallunterscheidung machen. Wir erhalten
Nach Abschnitt 9.5.2 haben die Eigenfunktionen des Bahndrehimpulsoperators
 folgende Form
folgende Form
wobei zu jedem  ein Eigenwert
ein Eigenwert 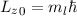 gehört. Dies ist eine
Produktwellenfunktion, bei der die Variable
gehört. Dies ist eine
Produktwellenfunktion, bei der die Variable 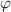 von den Variablen
von den Variablen  und
und 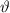 separiert ist. Sowohl das System der Funktionen
separiert ist. Sowohl das System der Funktionen 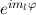 , als auch das
System der Funktionen
, als auch das
System der Funktionen 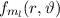 muss Orthogonalitätseigenschaften
haben. Näheres folgt im Kapitel 11 über das Wasserstoffatom. Die
Funktionen
muss Orthogonalitätseigenschaften
haben. Näheres folgt im Kapitel 11 über das Wasserstoffatom. Die
Funktionen 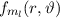 hängen vom betrachteten System ab. Für das System
der Funktionen
hängen vom betrachteten System ab. Für das System
der Funktionen 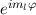 lässt sich die Orthogonalitätseigenschaft leicht
überprüfen
lässt sich die Orthogonalitätseigenschaft leicht
überprüfen
Häufig gehören zu einem Eigenwert  eines Operators
eines Operators 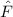 mehrere verschiedene
Eigenfunktionen. In diesem Fall spricht man von Entartung.
mehrere verschiedene
Eigenfunktionen. In diesem Fall spricht man von Entartung.
Zum Beispiel sind die Eigenfunktionen 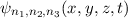 des Hamilton-Operators
eines in einem Würfel eingesperrten Teilchens entartet
des Hamilton-Operators
eines in einem Würfel eingesperrten Teilchens entartet
mit den Eigenwerten
Entartet sind dabei sicher alle Energieniveaus bei denen mindestens zwei der
Quantenzahlen 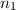 ,
, 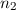 und
und 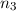 nicht verschieden sind. Aus dem Beweis des
Satzes 9.3 geht hervor, dass zwei verschiedene Eigenfunktionen, die zum
selben Eigenwert gehören nicht notwendigerweise orthogonal sind. Deshalb ist
Satz 9.3 im Fall der Entartung mit Vorsicht anzuwenden. Wir werden auf
diese Thematik der Entartung im nächsten Abschnitt nochmals genauer
eingehen.
nicht verschieden sind. Aus dem Beweis des
Satzes 9.3 geht hervor, dass zwei verschiedene Eigenfunktionen, die zum
selben Eigenwert gehören nicht notwendigerweise orthogonal sind. Deshalb ist
Satz 9.3 im Fall der Entartung mit Vorsicht anzuwenden. Wir werden auf
diese Thematik der Entartung im nächsten Abschnitt nochmals genauer
eingehen.
Für Eigenfunktionen zum selben Eigenwert, d.h. im Fall der Entartung, gilt der folgende Satz:
Satz 9.4 Eine Linearkombination von Eigenfunktionen des Operators 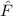 zum
selben Eigenwert
zum
selben Eigenwert 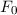 ist wieder eine Eigenfunktion des Operators
ist wieder eine Eigenfunktion des Operators 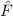 zum
selben Eigenwert
zum
selben Eigenwert 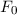 .
.
Beweis:
Seien 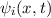 ,
,  = 1, 2, ...,
= 1, 2, ..., 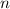 , Eigenfunktionen des Operators
, Eigenfunktionen des Operators 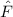 zum selben
Eigenwert
zum selben
Eigenwert  , dann gilt
, dann gilt
Für eine Linearkombination dieser Eigenfunktionen 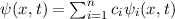 ,
,
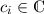 erhalten wir
erhalten wir

Im letzten Abschnitt haben wir gesehen, dass Eigenfunktionen zum selben
Eigenwert nicht notwendigerweise orthogonal sind. Im Allgemeinen ist es jedoch
sehr hilfreich mit orthogonalen Eigenfunktionen rechnen zu können. Nach
Satz 9.4 ist es nun möglich aus Eigenfunktionen 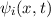 ,
,  = 1, 2, ...,
= 1, 2, ...,
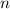 , zum selben Eigenwert
, zum selben Eigenwert 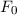 eines Operators
eines Operators 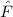 neue Eigenfunktionen
neue Eigenfunktionen
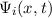 ,
,  = 1, 2, ...,
= 1, 2, ..., 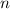 , zum selben Eigenwert
, zum selben Eigenwert 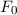 zu bilden, welche
orthogonal sind. Eine Methode, die es ermöglicht aus ursprünglich nicht
orthogonalen (normierten) Eigenfunktionen
zu bilden, welche
orthogonal sind. Eine Methode, die es ermöglicht aus ursprünglich nicht
orthogonalen (normierten) Eigenfunktionen 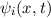 ,
,  = 1, 2, ...,
= 1, 2, ...,  ,
orthogonale (normierte) Eigenfunktionen
,
orthogonale (normierte) Eigenfunktionen 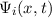 ,
,  = 1, 2, ...,
= 1, 2, ..., 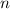 , zu gewinnen,
ist das sogenannte Gram-Schmidtsche Orthogonalisierungsverfahren. Die
neuen orthogonalen (normierten) Eigenfunktionen
, zu gewinnen,
ist das sogenannte Gram-Schmidtsche Orthogonalisierungsverfahren. Die
neuen orthogonalen (normierten) Eigenfunktionen 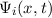 ,
,  = 1, 2, ...,
= 1, 2, ...,
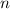 , ergeben sich dabei folgendermassen (für einen Beweis verweisen wir auf
Anhang C)
, ergeben sich dabei folgendermassen (für einen Beweis verweisen wir auf
Anhang C)
Nachdem wir nun Linearkombinationen von Eigenfunktionen, die zum selben
Eigenwert gehören, betrachtet haben, kommen wir nun zu Linearkombinationen von
Eigenfunktionen zu unterschiedlichen Eigenwerten. Genauer gesagt, gehen wir
der Frage nach, welche physikalische Bedeutung ein Zustand hat, der eine
Linearkombination von Eigenfunktionen des Operators 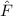 zu verschiedenen
Eigenwerten ist.
zu verschiedenen
Eigenwerten ist.
Wir starten als Beispiel mit den Eigenfunktionen des Hamilton-Operators für ein Teilchen im Potentialtopf. Nach Abschnitt 9.4.2 lauten die Eigenfunktionen
wobei
Wir bilden nun eine Linearkombination der Wellenfunktionen 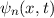
Jeder Summand von (9.274) ist eine Lösung der zeitabhängigen
Schrödinger-Gleichung (9.94). Dementsprechend ist nach dem Superpositionsprinzip
(siehe Abschnitt 9.4.1) auch die Linearkombination 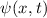 eine Lösung und stellt
damit einen Zustand dar, in dem sich das System befinden kann. Jedoch ist dieser
Zustand nicht stationär, denn
eine Lösung und stellt
damit einen Zustand dar, in dem sich das System befinden kann. Jedoch ist dieser
Zustand nicht stationär, denn 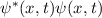 ist zeitabhängig, da sich die
Eigenwerte
ist zeitabhängig, da sich die
Eigenwerte 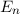 nach Voraussetzung unterscheiden.
nach Voraussetzung unterscheiden.
Wir kommen zu einer allgemeinen Betrachtung. Es sei 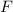 eine beliebige Observable
und die Funktionen
eine beliebige Observable
und die Funktionen 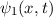 ,
, 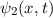 , ...,
, ..., 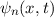 orthogonale Eigenfunktionen
des entsprechenden Operators
orthogonale Eigenfunktionen
des entsprechenden Operators 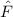 , die zu den Eigenwerten
, die zu den Eigenwerten 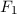 ,
, 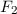 , ...,
, ...,
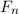 gehören, sodass die Eigenwertgleichungen
gehören, sodass die Eigenwertgleichungen 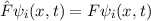 ,
,  =
1, 2, ...,
=
1, 2, ...,  , gelten. Wir betrachten eine beliebige Linearkombination der
Eigenfunktionen
, gelten. Wir betrachten eine beliebige Linearkombination der
Eigenfunktionen
und bestimmen den Erwartungswert der Observablen  , wenn sich das Teilchen im
Zustand
, wenn sich das Teilchen im
Zustand 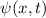 befindet. Es ergibt sich
befindet. Es ergibt sich
wobei wir im letzten Schritt die Normierung und die Orthogonalität der
Eigenfunktionen 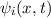 ,
,  = 1, 2, ...,
= 1, 2, ...,  , benützt haben. Dieser Ausdruck führt
zur folgenden Interpretation (siehe Postulat 3):
, benützt haben. Dieser Ausdruck führt
zur folgenden Interpretation (siehe Postulat 3):
Wenn sich ein Teilchen im Zustand 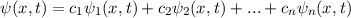 befindet, der eine Linearkombination der orthogonalen Eigenfunktionen
befindet, der eine Linearkombination der orthogonalen Eigenfunktionen 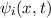 des
Operators
des
Operators 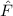 mit den Eigenwerten
mit den Eigenwerten 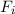 ist, dann ist die Wahrscheinlichkeit
ist, dann ist die Wahrscheinlichkeit 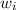 ,
dass eine Messung der Observablen
,
dass eine Messung der Observablen 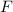 den Wert
den Wert 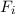 liefert, gegeben durch
liefert, gegeben durch
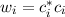 .
.
Diese Interpretation gilt auch bei Entartung, vorausgesetzt, dass die zu einem entarteten Eigenwert gehörenden Eigenfunktionen orthogonal sind. Die Konstruktion solcher orthogonaler Eigenfunktionen haben wir zu Beginn des Abschnitts skizziert (Gram-Schmidtsches Orthogonalisierungsverfahren).
Die Fourier-Reihe ist die Entwicklung einer periodischen Funktion nach einem speziellen orthogonalen Funktionensystem. Das analoge gilt für die Eigenfunktionen eines hermiteschen Operators:
Satz 9.5 Die Eigenfunktionen 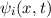 eines hermiteschen Operators
eines hermiteschen Operators 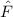 bilden auch ein orthogonales Funktionensystem. Erfüllt dieses System die
Vollständigkeitsrelation
bilden auch ein orthogonales Funktionensystem. Erfüllt dieses System die
Vollständigkeitsrelation
so lässt sich jeder Zustand 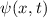 , in welchem sich das betrachtete quantenmechanische
System befinden kann, als Linearkombination dieser Eigenfunktionen
, in welchem sich das betrachtete quantenmechanische
System befinden kann, als Linearkombination dieser Eigenfunktionen 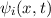 schreiben. Man spricht dann von einer Entwicklung der Wellenfunktion
schreiben. Man spricht dann von einer Entwicklung der Wellenfunktion 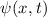 nach
den Eigenfunktionen
nach
den Eigenfunktionen 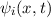 des Operators
des Operators 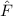 .
.
Beweis:
Es seien 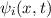 Eigenfunktionen des Operators
Eigenfunktionen des Operators 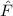 , welche die
Vollständigkeitsrelation (9.277) erfüllen, dann gilt für einen beliebigen Zustand
, welche die
Vollständigkeitsrelation (9.277) erfüllen, dann gilt für einen beliebigen Zustand
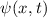 des betrachteten quantenmechanischen Systems
des betrachteten quantenmechanischen Systems

Als Illustration von Satz 9.5 ist im Anhang D die Entwicklung einer Dreiecksfunktion nach den Eigenfunktionen des Hamiltonoperators des Teilchens im Potentialtopf ausgeführt.
Zusammen mit der Interpretation aus dem letzten Abschnitt 9.5.6, lässt sich nun Postulat 3 folgendermassen präzisieren:
Das Ergebnis einer einzelnen Messung einer Observablen 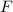 ist ein Eigenwert des
zugehörigen Operators
ist ein Eigenwert des
zugehörigen Operators 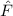 . Erhält man bei einer Messung den Eigenwert
. Erhält man bei einer Messung den Eigenwert 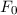 , so
geht die Wellenfunktion in die entsprechende Eigenfunktion
, so
geht die Wellenfunktion in die entsprechende Eigenfunktion 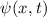 über.
D.h. befindet sich das System vor der Messung einer Observablen
über.
D.h. befindet sich das System vor der Messung einer Observablen  nicht in einem
Eigenzustand des entsprechenden Operators
nicht in einem
Eigenzustand des entsprechenden Operators  , so ändert die Messung den Zustand
des System, sodass sich das System nach der Messung in einem Eigenzustand des
Operators
, so ändert die Messung den Zustand
des System, sodass sich das System nach der Messung in einem Eigenzustand des
Operators  befindet. Die Wahrscheinlichkeit
befindet. Die Wahrscheinlichkeit 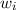 , welches Messresultat resultiert
und damit welcher Eigenzustand das System nach der Messung einnimmt, ist
bestimmt durch den Betrag der Koeffizienten
, welches Messresultat resultiert
und damit welcher Eigenzustand das System nach der Messung einnimmt, ist
bestimmt durch den Betrag der Koeffizienten 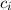 der Entwicklung des Zustands vor
der Messung nach den Eigenfunktionen des Operators
der Entwicklung des Zustands vor
der Messung nach den Eigenfunktionen des Operators  . Hingegen bleibt der
Zustand des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen
. Hingegen bleibt der
Zustand des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen  einem Eigenzustand des entsprechenden Operators
einem Eigenzustand des entsprechenden Operators 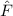 entspricht.
entspricht.
Der Formalismus, der hier am Beispiel der Bewegung eines einzelnen Teilchens
(Massenpunkt) entwickelt wurde, gilt auch für Systeme mit beliebig vielen
Freiheitsgraden. An die Stelle von  und
und 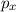 können auch die kanonisch
konjugierten Variablen
können auch die kanonisch
konjugierten Variablen 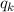 und
und 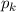 treten. Ausser Ort und Impuls eines Teilchens
können Paare von konjugierten Variablen auch andere physikalische Grössen
beschreiben, wie zum Beispiel elektrische Ladung und magnetischer Fluss oder
Teilchenzahl und Phase. Der Formalismus der Quantenmechanik gilt also sehr
allgemein im Konfigurationsraum eines physikalischen Systems.
treten. Ausser Ort und Impuls eines Teilchens
können Paare von konjugierten Variablen auch andere physikalische Grössen
beschreiben, wie zum Beispiel elektrische Ladung und magnetischer Fluss oder
Teilchenzahl und Phase. Der Formalismus der Quantenmechanik gilt also sehr
allgemein im Konfigurationsraum eines physikalischen Systems.
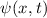 . Sie beschreibt den Zustand des Teilchens. Dabei
gibt
. Sie beschreibt den Zustand des Teilchens. Dabei
gibt 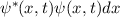 die Wahrscheinlichkeit an das Teilchen zur Zeit
die Wahrscheinlichkeit an das Teilchen zur Zeit 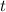 zwischen
zwischen  und
und 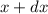 anzutreffen. Die Grösse
anzutreffen. Die Grösse 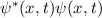 wird
daher als Wahrscheinlichkeitsdichte bezeichnet.
wird
daher als Wahrscheinlichkeitsdichte bezeichnet.
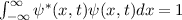 .
.
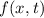 , die eine
physikalische Messgrösse beschreibt, ist für einen bestimmten Zeitpunkt
, die eine
physikalische Messgrösse beschreibt, ist für einen bestimmten Zeitpunkt
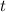 gegeben durch
gegeben durch 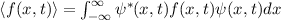 .
.
 kann auch der entsprechende Impuls
kann auch der entsprechende Impuls 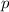 als Variable für die Wellenfunktion eingeführt werden und somit von der
Ortsraumdarstellung in die Impulsraumdarstellung übergehen.
als Variable für die Wellenfunktion eingeführt werden und somit von der
Ortsraumdarstellung in die Impulsraumdarstellung übergehen.
 und der Impuls
und der Impuls 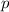 eines Teilchens nicht gleichzeitig beliebig
genau bestimmt. Dieses Eigenschaft der Quantenmechanik wird als
Heisenbergsche Unschärferelation bezeichnet und lautet mathematisch
ausgedrückt
eines Teilchens nicht gleichzeitig beliebig
genau bestimmt. Dieses Eigenschaft der Quantenmechanik wird als
Heisenbergsche Unschärferelation bezeichnet und lautet mathematisch
ausgedrückt 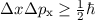 , wobei allgemein die Unschärfe
, wobei allgemein die Unschärfe 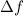 einer
Grösse
einer
Grösse 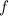 bestimmt ist durch die Standardabweichung, die durch
die Wurzel des Erwartungswerts der Quadrate der Abweichungen vom
Erwartungswert gegeben ist
bestimmt ist durch die Standardabweichung, die durch
die Wurzel des Erwartungswerts der Quadrate der Abweichungen vom
Erwartungswert gegeben ist 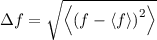 .
.
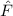 ist dabei definiert durch die Bedingung, dass für
eine Funktion
ist dabei definiert durch die Bedingung, dass für
eine Funktion 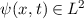 gilt
gilt 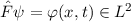 . Dabei bezeichnet
. Dabei bezeichnet
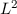 den Raum der quadratisch integrablen Funktionen. Zudem sind
quantenmechanische Operatoren linear, erfüllen das Distributiv- und
Assoziativgesetz, erüllen im Allgemeinen das Kommutativgesetz nicht und
besitzen reelle Erwartungswerte.
den Raum der quadratisch integrablen Funktionen. Zudem sind
quantenmechanische Operatoren linear, erfüllen das Distributiv- und
Assoziativgesetz, erüllen im Allgemeinen das Kommutativgesetz nicht und
besitzen reelle Erwartungswerte.
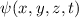 eines Teilchens bekannt, so ist der Zustand
des Teilchens vollständig charakterisiert. Insbesondere ist es möglich die
Erwartungswerte beliebiger Observablen auszurechnen und somit das Verhalten
des Teilchens in einem Experiment vorauszusagen. Wie nun aber die
Wellenfunktion
eines Teilchens bekannt, so ist der Zustand
des Teilchens vollständig charakterisiert. Insbesondere ist es möglich die
Erwartungswerte beliebiger Observablen auszurechnen und somit das Verhalten
des Teilchens in einem Experiment vorauszusagen. Wie nun aber die
Wellenfunktion 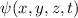 bestimmt wird, beantwortet das zweite Postulat
der Quantenmechanik: Die Wellenfunktion
bestimmt wird, beantwortet das zweite Postulat
der Quantenmechanik: Die Wellenfunktion 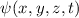 ist eine Lösung der
Differentialgleichung
ist eine Lösung der
Differentialgleichung
Diese Gleichung wird nach Schrödinger die zeitabhängige Schrödinger-Gleichung genannt.
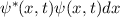 das Teilchen zwischen
das Teilchen zwischen  und
und 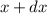 anzutreffen nicht von
der Zeit
anzutreffen nicht von
der Zeit 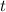 abhängt, heisst stationärer Zustand und hat im Allgemeinen die
Form
abhängt, heisst stationärer Zustand und hat im Allgemeinen die
Form 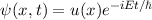 . Für die Funktion
. Für die Funktion 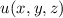 gilt dann die
zeitunabhängige Schrödinger-Gleichung
gilt dann die
zeitunabhängige Schrödinger-Gleichung
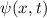 und
und 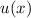 sind normierbar, streben mit
sind normierbar, streben mit 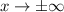 genügend rasch gegen null (dasselbe gilt auch für die Ableitungen nach
genügend rasch gegen null (dasselbe gilt auch für die Ableitungen nach  )
und sind für alle
)
und sind für alle  stetig, eindeutig und endlich (dasselbe gilt auch
für die Ableitungen nach
stetig, eindeutig und endlich (dasselbe gilt auch
für die Ableitungen nach  ). Zudem gilt das Superpositionsprinzip,
d.h. eine beliebige Linearkombination von Lösungen ist ebenfalls eine
Lösung.
). Zudem gilt das Superpositionsprinzip,
d.h. eine beliebige Linearkombination von Lösungen ist ebenfalls eine
Lösung.
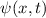 ist der Erwartungswert
ist der Erwartungswert  einer
Observablen
einer
Observablen 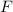 scharf bestimmt, wenn bei wiederholter Messung an
identisch gleich präparierten Teilchen immer der selbe Wert
scharf bestimmt, wenn bei wiederholter Messung an
identisch gleich präparierten Teilchen immer der selbe Wert 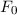 resultiert.
Mathematisch bedeutet das, dass die Unschärfe
resultiert.
Mathematisch bedeutet das, dass die Unschärfe 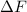 verschwinden muss
verschwinden muss
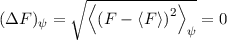 . Der Index
. Der Index 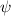 soll daran erinnern, dass diese
Beziehung für ein Teilchen im Zustand
soll daran erinnern, dass diese
Beziehung für ein Teilchen im Zustand 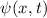 gilt, denn es hängt vom
Zustand ab, ob der Erwartungswert einer Observable einen scharfen Wert
annimmt oder nicht.
gilt, denn es hängt vom
Zustand ab, ob der Erwartungswert einer Observable einen scharfen Wert
annimmt oder nicht.
Mit Hilfe des Operatorformalismusses lässt sich eine einfache Bedingung
angeben, wann der Erwartungswert  einer Observable
einer Observable  im Zustand
im Zustand
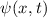 einen scharfen Wert besitzt: Sei der Zustand jedes betrachteten
Teilchens beschrieben durch die Wellenfunktion
einen scharfen Wert besitzt: Sei der Zustand jedes betrachteten
Teilchens beschrieben durch die Wellenfunktion 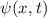 im Ortsraum, dann
gilt: Der Erwartungswert
im Ortsraum, dann
gilt: Der Erwartungswert 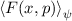 einer Observable
einer Observable 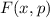 nimmt genau
dann den scharfen Wert
nimmt genau
dann den scharfen Wert 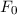 an, wenn die Wellenfunktion
an, wenn die Wellenfunktion 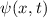 die Gleichung
die Gleichung 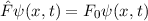 erfüllt. Diese Gleichung wird als
Eigenwertgleichung bezeichnet. Sie besagt, dass sich die Wellenfunktion
erfüllt. Diese Gleichung wird als
Eigenwertgleichung bezeichnet. Sie besagt, dass sich die Wellenfunktion
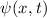 bis auf den Faktor
bis auf den Faktor 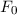 reproduziert, wenn man den Operator
reproduziert, wenn man den Operator 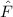 auf
sie anwendet. Eine Wellenfunktion
auf
sie anwendet. Eine Wellenfunktion 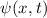 , die diese Gleichung erfüllt, ist
eine Eigenfunktion des Operators
, die diese Gleichung erfüllt, ist
eine Eigenfunktion des Operators 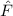 . Der scharfe Wert
. Der scharfe Wert 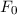 , den der
Erwartungswert
, den der
Erwartungswert 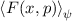 annimmt, wird Eigenwert des Operators
annimmt, wird Eigenwert des Operators 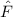 genannt.
genannt.
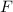 ist ein Eigenwert des zugehörigen
Operators
ist ein Eigenwert des zugehörigen
Operators 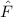 . Erhält man bei einer Messung den Eigenwert
. Erhält man bei einer Messung den Eigenwert 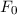 , so geht die
Wellenfunktion in die entsprechende Eigenfunktion
, so geht die
Wellenfunktion in die entsprechende Eigenfunktion 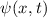 über. D.h. befindet
sich das System vor der Messung einer Observablen
über. D.h. befindet
sich das System vor der Messung einer Observablen 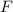 nicht in einem
Eigenzustand des entsprechenden Operators
nicht in einem
Eigenzustand des entsprechenden Operators 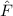 , so ändert die Messung den
Zustand des System, sodass sich das System nach der Messung in einem
Eigenzustand des Operators
, so ändert die Messung den
Zustand des System, sodass sich das System nach der Messung in einem
Eigenzustand des Operators 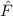 befindet. Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen
befindet. Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen 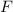 einem Eigenzustand des entsprechenden Operators
einem Eigenzustand des entsprechenden Operators 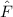 entspricht.
entspricht.
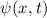 existieren, für die die Erwartungswerte
von zwei Observablen gleichzeitig scharf sind, beantwortet folgender
Satz: Die Erwartungswerte von zwei Observablen
existieren, für die die Erwartungswerte
von zwei Observablen gleichzeitig scharf sind, beantwortet folgender
Satz: Die Erwartungswerte von zwei Observablen  und
und  eines
Teilchens im Zustand
eines
Teilchens im Zustand 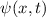 sind dann und nur dann gleichzeitig
scharf, wenn die Anwendung des Kommutators der entsprechenden
Operatoren
sind dann und nur dann gleichzeitig
scharf, wenn die Anwendung des Kommutators der entsprechenden
Operatoren 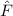 und
und 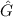 auf die Wellenfunktion
auf die Wellenfunktion 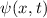 null ergibt, d.h.
null ergibt, d.h.
![[Fˆ, ˆG]ψ(x,t) = 0](PhysikIV3120x.png) .
.
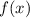 und
und 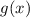 nennt man im Variablenbereich
nennt man im Variablenbereich 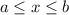 orthogonal, wenn gilt
orthogonal, wenn gilt 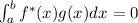 . Für die Wellenfunktionen
. Für die Wellenfunktionen 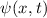 gilt der folgende Satz: Es seien
gilt der folgende Satz: Es seien 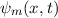 und
und 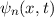 Eigenfunktionen des
hermiteschen Operators
Eigenfunktionen des
hermiteschen Operators 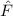 , die zu verschiedenen Eigenwerten
, die zu verschiedenen Eigenwerten 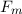 und
und 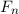 gehören. Dann sind
gehören. Dann sind 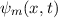 und
und 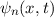 orthogonal in ihrem räumlichen
Existenzgebiet, d.h.
orthogonal in ihrem räumlichen
Existenzgebiet, d.h. 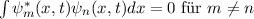 .
.
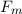 eines Operators
eines Operators 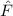 mehrere
verschiedene Eigenfunktionen. In diesem Fall spricht man von Entartung. In
diesem Fall gilt der folgende Satz: Eine Linearkombination von Eigenfunktionen
des Operators
mehrere
verschiedene Eigenfunktionen. In diesem Fall spricht man von Entartung. In
diesem Fall gilt der folgende Satz: Eine Linearkombination von Eigenfunktionen
des Operators 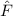 zum selben Eigenwert
zum selben Eigenwert 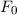 ist wieder eine Eigenfunktion des
Operators
ist wieder eine Eigenfunktion des
Operators 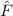 zum selben Eigenwert
zum selben Eigenwert 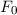 .
.
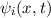 ,
,  = 1, 2, ...,
= 1, 2, ..., 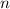 , zum selben
Eigenwert
, zum selben
Eigenwert 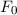 eines Operators
eines Operators 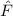 neue Eigenfunktionen
neue Eigenfunktionen 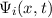 ,
,  = 1,
2, ...,
= 1,
2, ..., 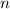 , zum selben Eigenwert
, zum selben Eigenwert 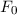 zu bilden, welche orthogonal
sind. Eine Methode, die dies ermöglicht ist das Gram-Schmidtsche
Orthogonalisierungsverfahren.
zu bilden, welche orthogonal
sind. Eine Methode, die dies ermöglicht ist das Gram-Schmidtsche
Orthogonalisierungsverfahren.
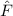 zu verschiedenen Eigenwerten ist, hat eine
physikalische Bedeutung, denn es gilt: Wenn sich ein Teilchen im Zustand
zu verschiedenen Eigenwerten ist, hat eine
physikalische Bedeutung, denn es gilt: Wenn sich ein Teilchen im Zustand
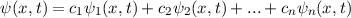 befindet, der eine
Linearkombination der orthogonalen Eigenfunktionen
befindet, der eine
Linearkombination der orthogonalen Eigenfunktionen 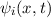 des Operators
des Operators
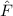 mit den Eigenwerten
mit den Eigenwerten 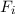 ist, dann ist die Wahrscheinlichkeit
ist, dann ist die Wahrscheinlichkeit 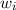 , dass eine
Messung der Observablen
, dass eine
Messung der Observablen 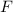 den Wert
den Wert 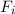 liefert, gegeben durch
liefert, gegeben durch
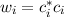 .
.
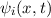 eines hermiteschen
Operators
eines hermiteschen
Operators 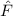 bilden auch ein orthogonales Funktionensystem. Erfüllt dieses
System die Vollständigkeitsrelation
bilden auch ein orthogonales Funktionensystem. Erfüllt dieses
System die Vollständigkeitsrelation 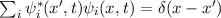 ,
so lässt sich jeder Zustand
,
so lässt sich jeder Zustand 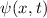 , in welchem sich das betrachtete
quantenmechanische System befinden kann, als Linearkombination dieser
Eigenfunktionen
, in welchem sich das betrachtete
quantenmechanische System befinden kann, als Linearkombination dieser
Eigenfunktionen 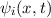 schreiben. Man spricht dann von einer Entwicklung
der Wellenfunktion
schreiben. Man spricht dann von einer Entwicklung
der Wellenfunktion 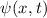 nach den Eigenfunktionen
nach den Eigenfunktionen 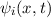 des Operators
des Operators
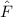 .
.
 ist ein
Eigenwert des zugehörigen Operators
ist ein
Eigenwert des zugehörigen Operators  . Erhält man bei einer Messung den
Eigenwert
. Erhält man bei einer Messung den
Eigenwert 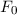 , so geht die Wellenfunktion in die entsprechende Eigenfunktion
, so geht die Wellenfunktion in die entsprechende Eigenfunktion
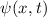 über. D.h. befindet sich das System vor der Messung einer
Observablen
über. D.h. befindet sich das System vor der Messung einer
Observablen 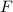 nicht in einem Eigenzustand des entsprechenden Operators
nicht in einem Eigenzustand des entsprechenden Operators
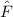 , so ändert die Messung den Zustand des System, sodass sich das System
nach der Messung in einem Eigenzustand des Operators
, so ändert die Messung den Zustand des System, sodass sich das System
nach der Messung in einem Eigenzustand des Operators 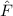 befindet. Die
Wahrscheinlichkeit
befindet. Die
Wahrscheinlichkeit 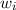 , welches Messresultat resultiert und damit welcher
Eigenzustand das System nach der Messung einnimmt, ist bestimmt durch den
Betrag der Koeffizienten
, welches Messresultat resultiert und damit welcher
Eigenzustand das System nach der Messung einnimmt, ist bestimmt durch den
Betrag der Koeffizienten 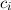 der Entwicklung des Zustands vor der Messung
nach den Eigenfunktionen des Operators
der Entwicklung des Zustands vor der Messung
nach den Eigenfunktionen des Operators 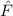 . Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen
. Hingegen bleibt der Zustand
des Systems unverändert, wenn dieser bereits vor der Messung der
Observablen  einem Eigenzustand des entsprechenden Operators
einem Eigenzustand des entsprechenden Operators  entspricht.
entspricht.