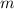 ,
welches an einer Feder mit Federkonstante
,
welches an einer Feder mit Federkonstante 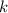 befestigt ist und Oszillationen um die
Ruhelage
befestigt ist und Oszillationen um die
Ruhelage 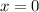 ausführt.
ausführt. In diesem Kapitel befassen wir uns mit den quantenmechanischen Eigenschaften eines der grundlegenden Modelle der Physik, dem harmonischen Oszillator. Ein harmonischer Oszillator ist ein physikalisches System in dem eine charakteristische Grösse, wie z.B. die Koordinate eines Teilchens, eine sinusförmige Zeitabhängigkeit zeigt, d.h. eine harmonische Schwingung ausführt. Diese Oszillationen werden durch eine in dieser charakteristischen Grösse linearen Rückstellkraft im Zusammenspiel mit der Trägheit des Systems verursacht. In der Natur gibt es sehr viele physikalische Systeme, die in guter Näherung als ein solches lineares Schwingungssystem betrachtet werden können: Mechanische Oszillatoren, z.B. das Federpendel, elektrische Oszillatoren, z.B. der LC-Schwingkreis, die Schwingungen zweiatomiger Moleküle oder Gitterschwingungen in einem Festkörper, um nur einige zu nennen.
Hier beginnen wir mit der klassischen Bewegungsgleichung eines harmonischen Oszillators, die wir für das Beispiel des Federpendels formulieren. Es folgt dann die quantenmechanische Behandlung des harmonischen Oszillators, bei der wir die zugehörige Schrödinger-Gleichung lösen. Zum Abschluss des Kapitels vergleichen wir den klassischen mit dem quantenmechanischen Oszillator.
Wir betrachten ein Federpendel (siehe Abb. 10.1), d.h. ein Teilchen der Masse 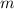 ,
welches an einer Feder mit Federkonstante
,
welches an einer Feder mit Federkonstante 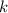 befestigt ist und Oszillationen um die
Ruhelage
befestigt ist und Oszillationen um die
Ruhelage 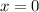 ausführt.
ausführt.
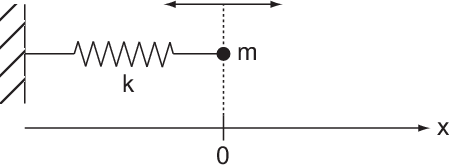
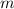 ist an einer Feder mit
Federkonstante
ist an einer Feder mit
Federkonstante 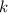 befestigt und führt Oszillationen um die Ruhelage
befestigt und führt Oszillationen um die Ruhelage 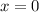 aus.
aus.Diese Schwingung um die Ruhelage kommt aufgrund der durch die Feder bewirkten
linearen Kraft zustande. Diese Kraft wird Rückstellkraft genannt, da sie in
jedem Punkt auf der x-Achse in Richtung Ruhelage zeigt und somit bei einer
Auslenkung das Teilchen wieder in Richtung der Ruhelage zwingt. Für ein
Federpendel ist diese Rückstellkraft 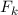 durch das sogenannte Hookesche Gesetz
gegeben
durch das sogenannte Hookesche Gesetz
gegeben
Sie ist wie bereits erwähnt linear in der Auslenkung  aus der Ruhelage. Die
klassische Bewegungsgleichung lautet demzufolge
aus der Ruhelage. Die
klassische Bewegungsgleichung lautet demzufolge
Die Lösung dieser Differentialgleichung ist eine harmonische Schwingung bei der
Kreisfrequenz 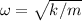
mit Amplitude 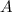 und der Phase
und der Phase 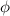 , die von den Anfangsbedingungen abhängen.
Die Lösung verdeutlicht noch einmal, dass bei einem harmonischen Oszillator die
Frequenz
, die von den Anfangsbedingungen abhängen.
Die Lösung verdeutlicht noch einmal, dass bei einem harmonischen Oszillator die
Frequenz 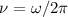 unabhängig von der Amplitude
unabhängig von der Amplitude 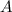 ist.
ist.
Diese grundlegenden Eigenschaften, die wir am Beispiel des Federpendels kennengelernt haben, liegen allen Systemen, welche durch ein Oszillatormodell beschrieben werden können, zugrunde. Jedes solche System führt eine Oszillation um eine Ruhelage, bewirkt durch eine lineare Rückstellkraft, aus, wobei die Oszillationsfrequenz für genügend kleine Auslenkungen unabhängig von der Amplitude ist.
Wie zu Beginn erwähnt, lassen sich zahlreiche physikalische Systeme angenähert als
harmonische Oszillatoren beschreiben. Jedoch sind in realen Systemen die
Rückstellkräfte häufig bei grösseren Auslenkungen nicht linear. Diese Nichtlinearität
führt zu anharmonischen Oszillationen, bei denen das System Schwingungen bei einer
Reihe von Frequenzen ausführt. In anderen Worten ein idealer harmonischer
Oszillator, bei dem die Rückstellkraft für beliebig grosse Auslenkungen linear
in der Auslenkung aus der Ruhelage ist, existiert nicht. Dennoch kann die
Rückstellkraft auch für solche Systeme für genügend kleine Auslenkungen aus der
Ruhelage linearisiert werden. Mathematisch bedeutet diese Linearisierung,
dass die Rückstellkraft 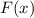 um die Ruhelage
um die Ruhelage 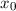 bis zum linearen Term
(Taylor-)entwickelt wird
bis zum linearen Term
(Taylor-)entwickelt wird
wobei wir verwendet haben, dass in der Ruhelage 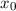 keine Kraft auf das Teilchen
wirkt, d.h.
keine Kraft auf das Teilchen
wirkt, d.h. 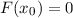 . Wenn alle anderen Terme in dieser Entwicklung ausreichend
klein sind, so lässt sich das System in guter Näherung als harmonischer Oszillator
beschreiben.
. Wenn alle anderen Terme in dieser Entwicklung ausreichend
klein sind, so lässt sich das System in guter Näherung als harmonischer Oszillator
beschreiben.
Die Schrödinger-Gleichung lautet
Das Potential 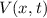 (siehe Abb. 10.2) ergibt sich dabei aus der Integration über
die Rückstellkraft
(siehe Abb. 10.2) ergibt sich dabei aus der Integration über
die Rückstellkraft 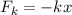
Wir sehen, dass das Potential zeitunabhängig ist und betrachten deshalb die zeitunabhängige Schrödinger-Gleichung
Diese Differentialgleichung lässt sich z.B. mit Hilfe eines Potenzreihenansatzes lösen (siehe Anhang E).
Hier betrachten wir jedoch eine häufig verwendete Lösungsmethode, bei der zunächst sogenannte Erzeugungs- und Vernichtungsoperatoren eingeführt werden. Dazu schreiben wir die zeitunabhängige Schrödinger-Gleichung um, indem wir die beiden Operatoren
einführen, wobei 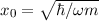 die Oszillatoramplitude normiert.
die Oszillatoramplitude normiert.
Bevor wir die Schrödinger-Gleichung umschreiben, gehen wir zuerst auf einige
wichtige Eigenschaften der Operatoren 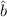 und
und 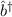 ein:
ein:
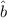 und
und 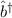 sind nicht hermitesch. Jedoch ist
sind nicht hermitesch. Jedoch ist 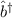 der adjungierte Operator zu
der adjungierte Operator zu 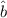 :
:
Dass die Relation (10.10) für die Operatoren 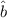 und
und 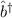 erfüllt ist, zeigt
folgende Rechnung
erfüllt ist, zeigt
folgende Rechnung
Partielle Integration für den zweiten Summanden liefert
Einsetzen in (10.11) ergibt
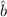 und
und 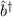 erfüllen die folgenden Kommutatorrelationen
erfüllen die folgenden Kommutatorrelationen
D.h. es gilt ![[ˆb†,ˆb] = - 1](PhysikIV3236x.png) . Analog folgen
. Analog folgen
Wir kommen nun zurück zu unserem ursprünglichen Ziel, der Formulierung der
Schrödinger-Gleichung (10.7) mit Hilfe der Operatoren 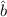 und
und 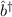 . Wir berechnen
dazu den Ausdruck
. Wir berechnen
dazu den Ausdruck 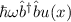 . Es ergibt sich mit
. Es ergibt sich mit 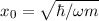 (siehe
Berechnung (10.14))
(siehe
Berechnung (10.14))
Damit hat die Schrödinger-Gleichung des harmonischen Oszillators ausgedrückt in
den Operatoren 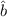 und
und 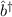 die folgende Form
die folgende Form
Wir gehen noch einen Schritt weiter und schreiben
D.h. die Eigenfunktionen 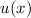 des Hamilton-Operators sind Eigenfunktionen des
Operators
des Hamilton-Operators sind Eigenfunktionen des
Operators 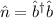 zum Eigenwert
zum Eigenwert 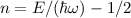 . Später werden wir erkennen,
dass der Erwartungswert des Operators
. Später werden wir erkennen,
dass der Erwartungswert des Operators 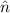 der Anzahl
der Anzahl 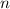 der Quanten
der Quanten 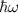 des
harmonischen Oszillators entspricht.
des
harmonischen Oszillators entspricht.
Unser nächstes Ziel ist nun die Bestimmung der Eigenfunktionen 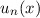 und der
entsprechenden Eigenwerte
und der
entsprechenden Eigenwerte 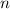 des Operators
des Operators 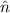 . Die Eigenfunktionen
. Die Eigenfunktionen 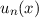 sind identisch mit denen des Hamilton-Operators und die entsprechenden
Energieeigenwerte
sind identisch mit denen des Hamilton-Operators und die entsprechenden
Energieeigenwerte  ergeben sich dann zu
ergeben sich dann zu
Dabei haben wir die Quantenzahl 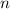 für die Eigenfunktionen
für die Eigenfunktionen 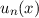 und die
Energieeigenwerte
und die
Energieeigenwerte  eingeführt.
eingeführt.
Wir bestimmen den Grundzustand des Operators 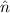 , d.h. die Eigenfunktion
, d.h. die Eigenfunktion 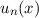 zum niedrigst möglichen Eigenwert
zum niedrigst möglichen Eigenwert 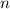 . Dazu müssen wir als erstes den niedrigst
möglichen Eigenwert bestimmen. Da der Operator
. Dazu müssen wir als erstes den niedrigst
möglichen Eigenwert bestimmen. Da der Operator 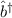 der adjungierte Operator von
der adjungierte Operator von
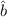 ist, gilt
ist, gilt
Demzufolge ist der niedrigstmögliche Eigenwert 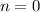 . Nach (10.22) muss dann
für die entsprechende Eigenfunktion
. Nach (10.22) muss dann
für die entsprechende Eigenfunktion 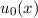 gelten
gelten 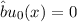 , d.h. wir
erhalten folgende Differentialgleichung zur Bestimmung des Grundzustands
, d.h. wir
erhalten folgende Differentialgleichung zur Bestimmung des Grundzustands
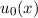
Wir wählen den Ansatz 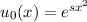 und erhalten für die Bestimmung der
Konstanten
und erhalten für die Bestimmung der
Konstanten  die Gleichung
die Gleichung 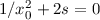 mit der Lösung
mit der Lösung 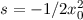 . Damit
ergibt sich
. Damit
ergibt sich
Die Konstante 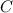 ergibt sich aus der Normierungsbedingung
ergibt sich aus der Normierungsbedingung
zu 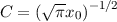 . Damit erhalten wir für den Grundzustand
. Damit erhalten wir für den Grundzustand 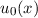 den
folgenden Ausdruck (siehe Abb. 10.3)
den
folgenden Ausdruck (siehe Abb. 10.3)
Zur Bestimmung der weiteren Eigenfunktionen 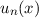 zeigen wir zwei kleine
Sätze.
zeigen wir zwei kleine
Sätze.
Satz 10.1 Ist 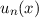 Eigenfunktion von
Eigenfunktion von 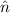 zum Eigenwert
zum Eigenwert 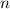 , so ist
, so ist 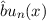 eine
Eigenfunktion von
eine
Eigenfunktion von 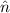 zum Eigenwert
zum Eigenwert 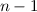 , d.h. der Operator
, d.h. der Operator 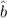 erniedrigt den
Eigenwert
erniedrigt den
Eigenwert 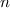 um 1. Daher wird
um 1. Daher wird 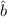 Vernichtungsoperator genannt. Für die
normierte Eigenfunktion
Vernichtungsoperator genannt. Für die
normierte Eigenfunktion 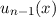 gilt
gilt
Beweis:
Wir wenden den Operator 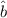 auf die Eigenwertgleichung (10.20) an
auf die Eigenwertgleichung (10.20) an
Mit 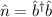 und (10.15) erhalten wir
und (10.15) erhalten wir
Mit
folgt für die normierte Eigenfunktion 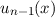

Der entsprechende Satz für den Operator 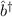 lautet:
lautet:
Satz 10.2 Ist 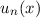 Eigenfunktion von
Eigenfunktion von 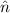 zum Eigenwert
zum Eigenwert 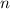 , so ist
, so ist 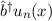 eine Eigenfunktion von
eine Eigenfunktion von 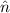 zum Eigenwert
zum Eigenwert 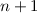 , d.h. der Operator
, d.h. der Operator 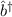 erhöht den
Eigenwert
erhöht den
Eigenwert 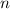 um 1. Daher wird
um 1. Daher wird 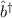 Erzeugungsoperator genannt. Für die
normierte Eigenfunktion
Erzeugungsoperator genannt. Für die
normierte Eigenfunktion 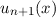 gilt
gilt
Beweis:
Wir wenden den Operator 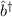 auf die Eigenwertgleichung (10.20) an
auf die Eigenwertgleichung (10.20) an
Mit 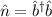 und (10.14) erhalten wir
und (10.14) erhalten wir
Mit
folgt für die normierte Eigenfunktion 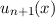

Nach Satz 10.2 ergeben sich nun die Eigenfunktionen 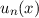 zu den Eigenwerten
zu den Eigenwerten 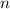 = 1, 2, 3, ... durch Anwendung von
= 1, 2, 3, ... durch Anwendung von 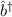 auf
auf 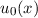
Wir zeigen nun, dass wir damit alle Eigenfunktionen gefunden haben, d.h. wir beweisen den folgenden Satz:
Satz 10.3 Mit 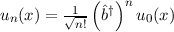 ,
, 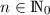 , haben wir alle
Eigenfunktionen des Operators
, haben wir alle
Eigenfunktionen des Operators 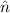 gefunden.
gefunden.
Widerspruchsbeweis:
Wir nehmen an, dass ein Eigenwert 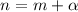 mit
mit 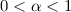 und
und 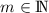 existiert und zeigen, dass diese Annahme auf einen Widerspruch führt. Die
Eigenwertgleichung lautet
existiert und zeigen, dass diese Annahme auf einen Widerspruch führt. Die
Eigenwertgleichung lautet
Mit (10.27) folgt
Dies steht im Widerspruch zur Positivität der Eigenwerte von  .
.

Fassen wir die Abschnitte 10.2.2 und 10.2.3 zusammen:
Die Eigenfunktionen 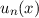 des Hamilton-Operators des harmonischen Oszillators
lauten (siehe Abb. 10.4)
des Hamilton-Operators des harmonischen Oszillators
lauten (siehe Abb. 10.4)
mit den Energieeigenwerten (siehe Tab. 10.1)
Insbesondere sind die Eigenfunktionen 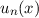 reell und je grösser die Anzahl
der Nullstellen der Eigenfunktionen ist, umso höher liegt der entsprechende
Energieeigenwert. Diese Regel gilt allgemein bei eindimensionalen Problemen.
reell und je grösser die Anzahl
der Nullstellen der Eigenfunktionen ist, umso höher liegt der entsprechende
Energieeigenwert. Diese Regel gilt allgemein bei eindimensionalen Problemen.
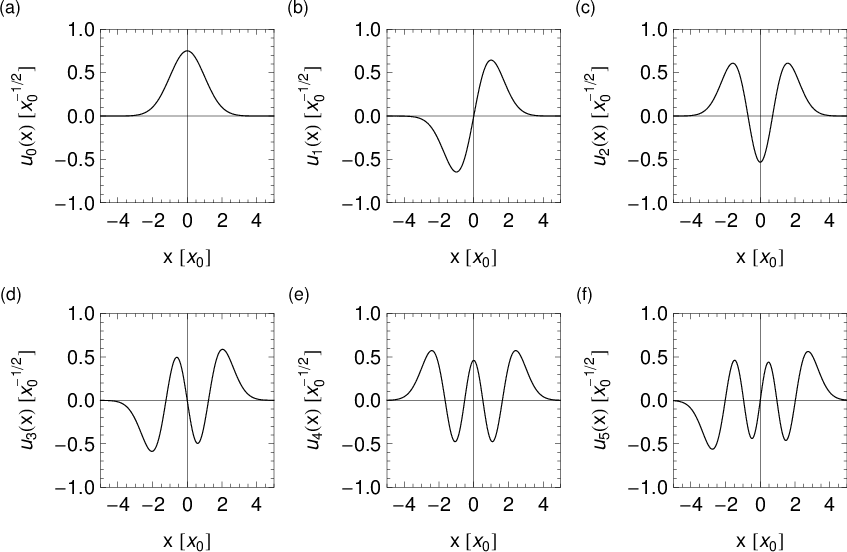
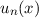 des harmonischen Oszillators für die
Quantenzahlen (a)
des harmonischen Oszillators für die
Quantenzahlen (a) 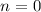 , (b)
, (b) 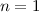 , (c)
, (c) 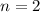 , (d)
, (d) 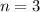 , (e)
, (e)  und
(f)
und
(f) 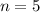 als Funktion der Ortskoordinate
als Funktion der Ortskoordinate  .
.Die Eigenfunktionen  lassen sich durch die sogenannten Hermite-Poly-nome
lassen sich durch die sogenannten Hermite-Poly-nome
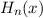 ausdrücken (siehe Anhang I.1). Es gilt
ausdrücken (siehe Anhang I.1). Es gilt
wobei die Hermite-Polynome 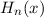 gegeben sind durch (siehe Tab. 10.1)
gegeben sind durch (siehe Tab. 10.1)
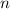 | 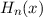 | 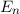 |
 | 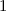 | 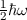 |
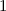 | 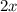 | 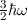 |
 | 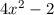 | 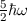 |
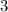 | 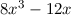 | 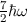 |
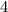 | 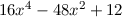 | 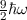 |
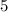 | 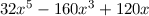 | 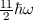 |
 |  |  |
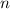 | 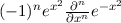 | 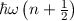 |
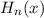 und die
entsprechenden Energieeigenwerten
und die
entsprechenden Energieeigenwerten 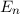 des harmonischen Oszillators.
des harmonischen Oszillators.Die niedrigste Energie des harmonischen Oszillators ist klassisch 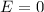 ,
quantenmechanisch
,
quantenmechanisch 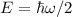 , d.h. im Gegensatz zur klassischen Mechanik
erhalten wir in der Quantenmechanik eine endliche Grundzustandsenergie, auch
Nullpunktsenergie genannt. In diesem Abschnitt gehen wir nun genauer auf diese
Nullpunktsenergie ein.
, d.h. im Gegensatz zur klassischen Mechanik
erhalten wir in der Quantenmechanik eine endliche Grundzustandsenergie, auch
Nullpunktsenergie genannt. In diesem Abschnitt gehen wir nun genauer auf diese
Nullpunktsenergie ein.
Wir bestimmen als erstes die Orts- und Impulsunschärfe 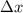 und
und 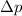 . Für den
Erwartungswert
. Für den
Erwartungswert 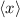 des Ortes erhalten wir
des Ortes erhalten wir
Demzufolge ergibt sich für die Ortsunschärfe 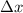
Analog erhalten wir für den Erwartungswert des Impulses  und die
Impulsunschärfe
und die
Impulsunschärfe 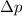
Damit erhalten wir im Grundzustand für die Orts- und Impulsunschärfe
Somit ist das Teilchen im Grundzustand nicht bei 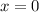 lokalisiert, sondern ist über
einen endlichen Bereich „verschmiert“, verbunden mit einem endlichen Impuls. Diesen
Sachverhalt wird Nullpunktsschwankung genannt.
lokalisiert, sondern ist über
einen endlichen Bereich „verschmiert“, verbunden mit einem endlichen Impuls. Diesen
Sachverhalt wird Nullpunktsschwankung genannt.
Wir leiten zusätzlich eine Ungleichung für die Nullpunktsenergie ausgehend von der Unschärferelation
her. Die Wellenfunktion werden wir dazu nicht explizit berechnen. Aus
Symmetriegründen gilt für den Grundzustand 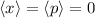 und somit
und somit
Damit erhalten wir für die Energie die folgende Ungleichung
Wir bestimmen das Minimum der rechten Seite der Ungleichung indem wir die
Ableitung nach 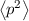 null setzen
null setzen
Auflösen nach 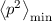 ergibt
ergibt
Damit lautet die Ungleichung für die Energie
Somit wird klar, dass die Nullpunktsenergie der kleinste Energiewert ist, der mit der Unschärferelation vereinbar ist.
Für die stationären Lösungen 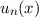 gilt nach (10.46)
gilt nach (10.46) 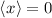 , d.h. in diesen
stationären Zuständen führt der harmonische Oszillator einzeln keine Oszillation aus.
Sie haben daher insbesondere nichts mit der klassischen Oszillationsbewegung
gemeinsam. Das Ziel ist es nun Lösungen der zeitabhängigen Schrödinger-Gleichung
zu bestimmen, die eine periodische Oszillation darstellen, d.h. Zustände in
denen der Erwartungswert des Ortes nicht verschwindet, sondern bzgl. der
Zeitabhängigkeit mit der klassischen Oszillationsbewegung übereinstimmt. Wir
gehen dazu von den Eigenzuständen
, d.h. in diesen
stationären Zuständen führt der harmonische Oszillator einzeln keine Oszillation aus.
Sie haben daher insbesondere nichts mit der klassischen Oszillationsbewegung
gemeinsam. Das Ziel ist es nun Lösungen der zeitabhängigen Schrödinger-Gleichung
zu bestimmen, die eine periodische Oszillation darstellen, d.h. Zustände in
denen der Erwartungswert des Ortes nicht verschwindet, sondern bzgl. der
Zeitabhängigkeit mit der klassischen Oszillationsbewegung übereinstimmt. Wir
gehen dazu von den Eigenzuständen 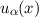 des Vernichtungsoperators
des Vernichtungsoperators 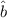 aus
aus
Wir entwickeln diese Zustände 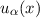 nach den stationären Zuständen
nach den stationären Zuständen 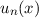 . Nach
Abschnitt 9.5.7 erhalten wir
. Nach
Abschnitt 9.5.7 erhalten wir
wobei für die Entwicklungskoeffizienten 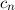 mit (9.278), (10.38), (10.58) und der
Eigenschaft, dass
mit (9.278), (10.38), (10.58) und der
Eigenschaft, dass 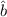 der adjungierte Operator von
der adjungierte Operator von 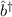 ist, gilt
ist, gilt
Damit folgt
Die Konstante 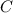 ergibt sich aus der Normierungsbedingung
ergibt sich aus der Normierungsbedingung
Damit erhalten wir
Einsetzen in (10.61) liefert für die Zustände 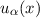 die folgende Entwicklung
die folgende Entwicklung
Die Zustände 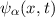 erhalten wir durch die Zeitentwicklung der stationären
Zustände
erhalten wir durch die Zeitentwicklung der stationären
Zustände 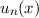
Mit 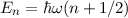 ergibt sich
ergibt sich
Die Zustände 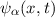 werden kohärente
Zustände1
genannt und sind Lösung der zeitabhängigen Schrödinger-Gleichung. Für den
Erwartungswert
werden kohärente
Zustände1
genannt und sind Lösung der zeitabhängigen Schrödinger-Gleichung. Für den
Erwartungswert 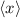 ergibt sich mit
ergibt sich mit 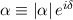
D.h. der Erwartungswert des Ortes führt eine periodische Oszillation aus. Wir haben also mit diesen kohärenten Zuständen, Zustände des harmonischen Oszillators gefunden, in denen der Erwartungswert des Ortes die selbe Zeitabhängigkeit wie die klassische Schwingung zeigt.
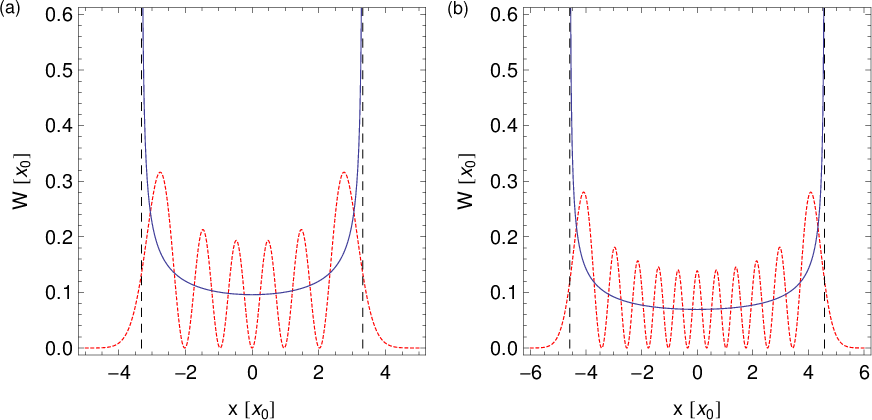
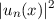 (rot gepunktete Linie) und die klassische Aufenthaltswahrscheinlichkeit
(rot gepunktete Linie) und die klassische Aufenthaltswahrscheinlichkeit 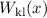 (blaue durchgezogene Linie) als Funktion der Ortskoordinate
(blaue durchgezogene Linie) als Funktion der Ortskoordinate  für die
Quantenzahlen (a)
für die
Quantenzahlen (a) 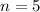 und (b)
und (b) 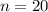 . Die schwarz gestrichelten Linien
markieren die klassischen Umkehrpunkte bei
. Die schwarz gestrichelten Linien
markieren die klassischen Umkehrpunkte bei 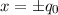 .
.Zum Abschluss dieses Kapitels vergleichen wir den quantenmechanischen mit dem klassischen harmonischen Oszillator. Die klassische Bewegung ist beschrieben durch
wobei 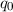 die Amplitude der Schwingung bezeichnet. Die klassische
Aufenthaltswahrscheinlichkeit
die Amplitude der Schwingung bezeichnet. Die klassische
Aufenthaltswahrscheinlichkeit 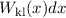 das Teilchen im Intervall
das Teilchen im Intervall ![[x,x + dx]](PhysikIV3448x.png) anzutreffen, ist gegeben durch
anzutreffen, ist gegeben durch
wobei 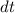 die Aufenthaltsdauer in
die Aufenthaltsdauer in 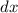 und
und 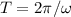 die Periode ist. Mit (10.68)
erhalten wir für
die Periode ist. Mit (10.68)
erhalten wir für 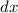 den Ausdruck
den Ausdruck
Einsetzen in (10.70) ergibt
Abb. 10.5 zeigt die quantenmechanische Aufenthaltswahrscheinlichkeit
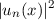 für die Quantenzahlen
für die Quantenzahlen 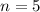 und
und 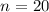 zusammen mit der
entsprechenden klassischen Aufenthaltswahrscheinlichkeit
zusammen mit der
entsprechenden klassischen Aufenthaltswahrscheinlichkeit 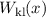 : Die klassische
Aufenthaltswahrscheinlichkeit
: Die klassische
Aufenthaltswahrscheinlichkeit 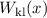 nimmt gegen die Umkehrpunkte
nimmt gegen die Umkehrpunkte
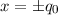 monoton zu (da sie umgekehrt proportional zur Geschwindigkeit ist).
Die quantenmechanische Aufenthaltswahrscheinlichkeit
monoton zu (da sie umgekehrt proportional zur Geschwindigkeit ist).
Die quantenmechanische Aufenthaltswahrscheinlichkeit 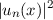 oszilliert,
wobei die Höhe der Maxima gegen die klassische Umkehrpunkte zunimmt.
Quantenmechanisch existiert zusätzlich eine endliche Wahrscheinlichkeit
das Teilchen bei Amplituden grösser als den klassischen Umkehrpunkten
oszilliert,
wobei die Höhe der Maxima gegen die klassische Umkehrpunkte zunimmt.
Quantenmechanisch existiert zusätzlich eine endliche Wahrscheinlichkeit
das Teilchen bei Amplituden grösser als den klassischen Umkehrpunkten
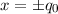 anzutreffen. Für sehr hohe Quantenzahlen
anzutreffen. Für sehr hohe Quantenzahlen 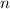 nähert sich die
quantenmechanische der klassischen Aufenthaltswahrscheinlichkeit an. Die
Oszillationen werden immer schwächer und die Wahrscheinlichkeit das Teilchen bei
Amplituden grösser als den klassischen Umkehrpunkten
nähert sich die
quantenmechanische der klassischen Aufenthaltswahrscheinlichkeit an. Die
Oszillationen werden immer schwächer und die Wahrscheinlichkeit das Teilchen bei
Amplituden grösser als den klassischen Umkehrpunkten 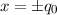 anzutreffen
sinkt.
anzutreffen
sinkt.
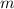 an einer Feder mit Federkonstante
an einer Feder mit Federkonstante 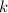 befestigt ist und Oszillationen
um die Ruhelage
befestigt ist und Oszillationen
um die Ruhelage 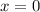 ausführt. Die klassische Bewegungsgleichung
eines solchen Teilchens lautet
ausführt. Die klassische Bewegungsgleichung
eines solchen Teilchens lautet 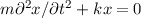 mit der Lösung
mit der Lösung
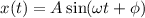 , wobei
, wobei 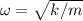 die Kreisfrequenz,
die Kreisfrequenz, 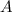 die
Amplitude und
die
Amplitude und 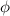 die Phase bezeichnen.
die Phase bezeichnen.
Daraus folgen die Eigenzustände
wobei 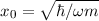 und die Energieeigenwerte
und die Energieeigenwerte
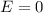 , quantenmechanisch
, quantenmechanisch 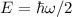 , d.h. im Gegensatz zur
klassischen Mechanik erhalten wir in der Quantenmechanik eine endliche
Grundzustandsenergie, auch Nullpunktsenergie genannt. Grund dafür
sind sogenannte Nullpunktsschwankungen, d.h. das Teilchen ist im
Grundzustand nicht bei
, d.h. im Gegensatz zur
klassischen Mechanik erhalten wir in der Quantenmechanik eine endliche
Grundzustandsenergie, auch Nullpunktsenergie genannt. Grund dafür
sind sogenannte Nullpunktsschwankungen, d.h. das Teilchen ist im
Grundzustand nicht bei 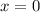 lokalisiert, sondern über einen endlichen
Bereich „verschmiert“, verbunden mit einem endlichen Impuls. Zudem ist die
Nullpunktsenergie der kleinste Energiewert, der mit der Unschärferelation
vereinbar ist.
lokalisiert, sondern über einen endlichen
Bereich „verschmiert“, verbunden mit einem endlichen Impuls. Zudem ist die
Nullpunktsenergie der kleinste Energiewert, der mit der Unschärferelation
vereinbar ist.
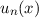 gilt
gilt  , d.h. in diesen stationären
Zuständen führt der harmonische Oszillator einzeln keine Oszillation aus. Sie
haben daher insbesondere nichts mit der klassischen Oszillationsbewegung
gemeinsam. Es lassen sich jedoch sogenannte kohärente Zustände
, d.h. in diesen stationären
Zuständen führt der harmonische Oszillator einzeln keine Oszillation aus. Sie
haben daher insbesondere nichts mit der klassischen Oszillationsbewegung
gemeinsam. Es lassen sich jedoch sogenannte kohärente Zustände 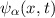 finden, in denen Erwartungswert des Orts eine periodische Oszillation ausführt
und somit die selbe Zeitabhängigkeit wie die klassische Schwingung
zeigt.
finden, in denen Erwartungswert des Orts eine periodische Oszillation ausführt
und somit die selbe Zeitabhängigkeit wie die klassische Schwingung
zeigt.
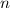 nähert sich die quantenmechanische der klassischen
Aufenthaltswahrscheinlichkeit an.
nähert sich die quantenmechanische der klassischen
Aufenthaltswahrscheinlichkeit an.