
In den letzten Kapiteln haben wir gelernt, dass elektromagnetische Strahlung sowohl Wellen- als auch Teilcheneigenschaften zeigt. Dabei ist die Wahrscheinlichkeit an einem gegebenen Ort ein Photon anzutreffen proportional zum Quadrat der Amplitude der klassischen elektromagnetischen Welle.
In diesem Kapitel diskutieren wir, wie sich auch bei massebehafteten Teilchen, wie z.B. Elektronen, Protonen, Neutronen, Atomkernen, ganzen Atomen oder auch Molekülen, nicht nur Teilcheneigenschaften sondern auch Welleneigenschaften beobachten lassen. Dabei werden wir in Analogie zum Photon experimentelle Beobachtungen erklären, indem wir annehmen, dass die Aufenthaltswahrscheinlichkeit materieller Teilchen proportional zum Quadrat der Amplitude einer Welle, der sogenannten Materiewelle, ist.
Im Gegensatz zur elektromagnetischen Welle, die dem Photon zugeordnet ist, kann die Materiewelle jedoch nicht mit der klassischen Theorie gedeutet werden. Die Materiewelle ist ein mathematisches Konzept zur Berechnung der Aufenthaltswahrscheinlichkeit eines massebehafteten Teilchens.
Materiewellen wurden 1923 von Louis de Broglie postuliert. Experimentelle Hinweise dafür, dass sich Teilchen wie Wellen verhalten können, gab es zu dieser Zeit aber noch nicht. De Broglies Idee entstand aus der Analogie zu den Photonen. Aufgrund dieser Analogie konnte er die Wellenlänge für Materiewellen angeben.
Diese Beziehung wird de Broglie-Beziehung genannt, wobei 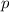 den Impuls des durch
die Materiewelle beschriebenen Teilchens bezeichnet und
den Impuls des durch
die Materiewelle beschriebenen Teilchens bezeichnet und 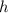 das Plancksche
Wirkungsquantum ist.
das Plancksche
Wirkungsquantum ist.
Für Photonen gilt wie bereits bekannt
wobei 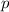 der Impuls des Photons ist. Dabei ist zu bedenken, dass Photonen sich
immer mit Lichtgeschwindigkeit ausbreiten und keine Ruhemasse haben. Aus diesem
Grund ist die Ruheenegie des Photons gleich null. Auch dieser Aspekt unterscheidet
Photonen von massebehafteten Teilchen.
der Impuls des Photons ist. Dabei ist zu bedenken, dass Photonen sich
immer mit Lichtgeschwindigkeit ausbreiten und keine Ruhemasse haben. Aus diesem
Grund ist die Ruheenegie des Photons gleich null. Auch dieser Aspekt unterscheidet
Photonen von massebehafteten Teilchen.
Im folgenden Abschnitt gehen wir nun auf experimentelle Situationen ein unter denen sich die Welleneigenschaften von Materie beobachten lassen.
Obwohl die Materiewelle kein klassisches Pendant hat und wir sie als mathematisches Konzept bezeichnet haben, zeigt sich die Realität der Materiewelle im Experiment.
Das erste Experiment, das den Wellencharakter bewegter Materieteilchen zum Vorschein brachte, wurde in den Jahren 1923 - 1927 (anfänglich ohne Kenntnis des de Broglieschen Postulats) von Clinton Davisson und Lester Germer in einem Industrielabor (Bell Telephone Laboratories) durchgeführt. Die beiden Experimentatoren arbeiteten am Problem der Sekundärelektronenemission, das für die Technik von Radioröhren von Bedeutung war.
Davisson und Germer schossen in ihrem Experiment (siehe Abb. 6.1) Elektronen
auf die Oberfläche von Ni-Kristallen und beobachteten die vom Kristall
ausgehenden Elektronen als Funktion des Winkels 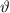 und als Funktion der
Beschleunigungsspannung
und als Funktion der
Beschleunigungsspannung 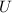 im Bereich zwischen 30 und 200 V.
im Bereich zwischen 30 und 200 V.
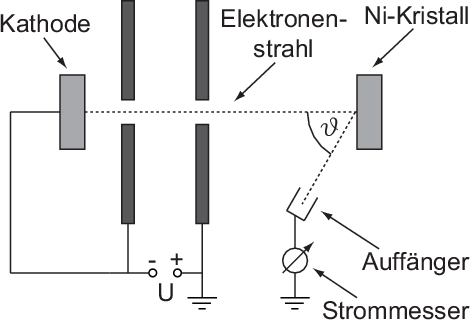
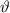 und der Beschleunigungsspannung
und der Beschleunigungsspannung 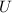 .
.Bei Beschleunigungsspannungen in diesem Bereich handelt es sich um relativ langsame Elektronen. Diese werden von den Atomen sehr stark gestreut, da sie sich aufgrund ihrer niedrigen Geschwindigkeit beim Streuprozess lange im Kraftfeld des streuenden Atoms befinden. Folglich dringen sie nicht in den Kristall ein, sondern werden von den Atomen an der Oberfläche gestreut. Die Beugung findet also in diesem Fall an einem Flächengitter und nicht an einem Raumgitter statt und unterscheidet sich deshalb von der Bragg-Reflexion (siehe Abschnitt 3.4.2), die restriktiver1 ist.
Wir betrachten die Beugung des Elektronenstrahls an den Atomreihen der Oberfläche, die ein Reflexionsgitter bilden (siehe Abb. 6.2). Wenn nun die einfallende Strahlung Wellennatur hat und an diesem Gitter gebeugt wird, dann treten Maxima der reflektierten Strahlung auf, wenn die von den einzelnen Atomreihen gestreuten Wellen konstruktiv interferieren, d.h. wenn gilt
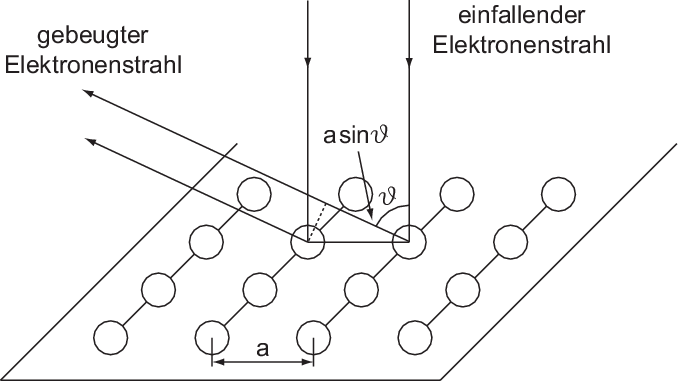
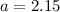 Å . Der Gangunterschied
zwischen zwei an benachbarten Atomen gebeugten Elektronenstrahlen beträgt
Å . Der Gangunterschied
zwischen zwei an benachbarten Atomen gebeugten Elektronenstrahlen beträgt
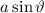 .
.Bei einer Beschleunigungsspannung von 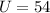 V beobachteten Davisson und
Germer bei senkrechtem Elektroneneinfall auf eine Kristallfläche, deren Orientierung
in Bezug auf das Kristallgitter bekannt war, ein erstes Maximum (
V beobachteten Davisson und
Germer bei senkrechtem Elektroneneinfall auf eine Kristallfläche, deren Orientierung
in Bezug auf das Kristallgitter bekannt war, ein erstes Maximum (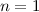 ) des
Auffängerstroms bei der Winkelstellung
) des
Auffängerstroms bei der Winkelstellung 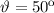 . Der Abstand der Atomreihen
. Der Abstand der Atomreihen  war aus Röntgen-Untersuchungen der Struktur bekannt. Für die spezielle
Kristallfläche des Experiments ist
war aus Röntgen-Untersuchungen der Struktur bekannt. Für die spezielle
Kristallfläche des Experiments ist 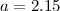 Å . Wenn man das Maximum als
Beugungsmaximum interpretiert, erhält man für den Elektronenstrahl folgende
Wellenlänge
Å . Wenn man das Maximum als
Beugungsmaximum interpretiert, erhält man für den Elektronenstrahl folgende
Wellenlänge
Wir überprüfen nun, ob diese Wellenlänge mit der de Broglie-Beziehung
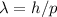 übereinstimmt. Der Impuls der Elektronen ergibt sich aus der
Beschleunigungsspannung
übereinstimmt. Der Impuls der Elektronen ergibt sich aus der
Beschleunigungsspannung 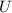 . Wir können dabei von nicht-relativistischen
Teilchen ausgehen, da bei den Experimenten von Davisson und Germer
. Wir können dabei von nicht-relativistischen
Teilchen ausgehen, da bei den Experimenten von Davisson und Germer 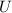 ausreichend niedrig war, so dass die Geschwindigkeit der Elektronen klein war im
Vergleich zur Lichtgeschwindigkeit (
ausreichend niedrig war, so dass die Geschwindigkeit der Elektronen klein war im
Vergleich zur Lichtgeschwindigkeit (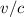 war von der Grössenordnung
war von der Grössenordnung 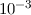 ).
Unter Vernachlässigung der Austrittsarbeit aus der Kathode folgt aus der
Energieerhaltung
).
Unter Vernachlässigung der Austrittsarbeit aus der Kathode folgt aus der
Energieerhaltung
Daraus erhalten wir für den Impuls 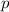 die Beziehung
die Beziehung
Einsetzen in die de Broglie-Beziehung ergibt für die Wellenlänge 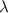
was mit dem Wert für die Wellenlänge aus dem Winkel für das Beugungsmaximum in guter Näherung übereinstimmt.
Bei der Streuung von Elektronen an Kristalloberflächen ist es wichtig Adsorption2 von Gas auf der Oberfläche zu vermeiden, da sonst die Eigenschaften der Adsorbatschicht das Streuexperiment beeinflussen können. Adsorption kann vermieden werden, indem die Oberflächen im Ultrahochvakuum untersucht werden. In den historischen Experimenten von Davisson und Germer waren diese Bedingungen nur angenähert erfüllt.
In denselben Jahren wurde von George Paget Thomson (dem Sohn von Joseph John
Thomson, dem Entdecker des Elektrons) und seinem Schüler A. Reid ein Experiment
mit der Absicht durchgeführt, die de Broglie-Beziehung zu prüfen. Im Gegensatz zu
Davisson und Germer benutzten diese Forscher nicht das Oberflächengitter, sondern
das Raumgitter von Kristallen zur Beugung, d.h. Bragg-Reflexion. Dazu ist es aber
notwendig, dass die Elektronen in das Gitter eindringen, d.h. man muss
schnelle Elektronen verwenden, was Beschleunigungsspannungen von der
Grössenordnung von 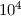 V entspricht. In diesem Experiment wird das Problem der
Oberflächenadsorption vermieden.
V entspricht. In diesem Experiment wird das Problem der
Oberflächenadsorption vermieden.
George Paget Thomson und Reid durchstrahlten sehr dünne Schichten von regellos orientierten Mikrokristallen, wie sie sich zum Beispiel beim Aufdampfen von Metallen im Hochvakuum auf dünne, amorphe, organische Filme ergeben (siehe Abb. 6.3). In einer solchen polykristallinen Schicht finden sich immer Kristalle, für welche die Bragg-Bedingung bei der betreffenden durch die Beschleunigungsspannung gegebenen de Broglie-Wellenlänge erfüllt ist. Auf diesen Zusammenhang werden wir im Rahmen der Untersuchung des Debye-Scherrer-Verfahrens zur Strukturanalyse polykristalliner Materialien mit Röntgen-Strahlung im Abschnitt 7.2.2 nochmals eingehen.
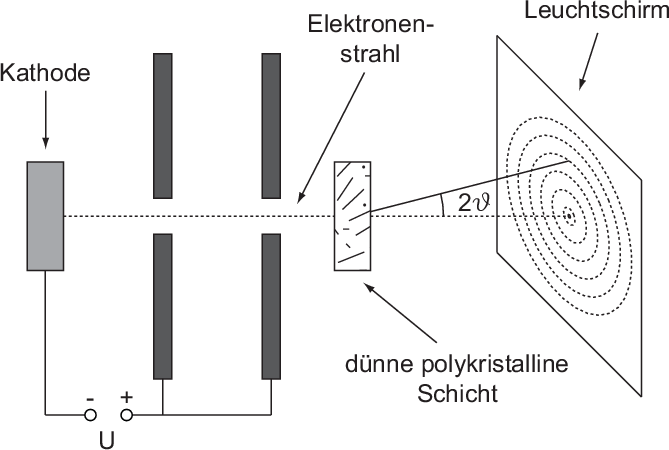
Für eine bestimmte Ordnung 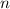 liegen die Maxima der gebeugten Strahlung auf
einem Kreis. Da verschiedene Ordnungen
liegen die Maxima der gebeugten Strahlung auf
einem Kreis. Da verschiedene Ordnungen 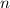 auftreten und da sich zudem
die Atome im Raumgitter auf verschiedene Art und Weise zu Netzebenen
zusammenfassen lassen, besteht das Beugungsbild aus vielen konzentrischen
Kreisen.
auftreten und da sich zudem
die Atome im Raumgitter auf verschiedene Art und Weise zu Netzebenen
zusammenfassen lassen, besteht das Beugungsbild aus vielen konzentrischen
Kreisen.
Bei bekannter Kristallstruktur, d.h. Gitterkonstante  , kann man aus dem
Bragg-Winkel
, kann man aus dem
Bragg-Winkel 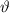 für ein Beugungsmaximum auf die Wellenlänge der Materiewellen
schliessen3.
für ein Beugungsmaximum auf die Wellenlänge der Materiewellen
schliessen3.
Wiederum kann man auch in diesem Experiment die Wellenlänge mit Hilfe der de
Broglie-Beziehung berechnen. Nur muss bei Beschleunigungsspannungen
von 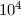 V und darüber der Impuls relativistisch berechnet werden. Unter
Vernachlässigung der Austrittsarbeit aus der Kathode gilt aufgrund der
Energieerhaltung
V und darüber der Impuls relativistisch berechnet werden. Unter
Vernachlässigung der Austrittsarbeit aus der Kathode gilt aufgrund der
Energieerhaltung
Diese Gleichung ist nach 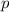 aufzulösen und das Ergebnis in die de Broglie-Beziehung
einzusetzen. George Paget Thomson und Reid erhielten befriedigende Übereinstimmung
zwischen dem Resultat dieser Berechnung und der aus dem Beugungsbild bestimmten
Wellenlänge.
aufzulösen und das Ergebnis in die de Broglie-Beziehung
einzusetzen. George Paget Thomson und Reid erhielten befriedigende Übereinstimmung
zwischen dem Resultat dieser Berechnung und der aus dem Beugungsbild bestimmten
Wellenlänge.
Diese beiden Experimente bestätigen die These, dass Elektronen Wellencharakter zeigen.
Beugung tritt immer auf, wenn zwischen den bewegten Materieteilchen und den Bausteinen des beugenden Objekts eine Wechselwirkung besteht. Im Fall der Elektronen, mit denen wir uns im letzten Abschnitt beschäftigt haben, ist in erster Linie die Coulomb-Wechselwirkung für die Streuung verantwortlich. Ebenfalls können magnetische Wechselwirkungen eine Rolle spielen, da das Elektron ein magnetisches Moment hat.
Am Beispiel der Neutronenbeugung zeigt sich, dass auch ungeladene Teilchen sich wie Wellen verhalten. Seit man in Kernreaktoren intensive Neutronenquellen zur Verfügung hat, ist die Neutronenbeugung zu einer der wichtigsten Methoden zur Untersuchung der Struktur von kondensierter4 Materie geworden.
Bei der Neutronenbeugung spielen zwei Wechselwirkungen, die von der gleichen Grössenordnung sein können, eine Rolle:
Wir untersuchen nun, welche Bedingung die Neutronen erfüllen müssen, damit Beugung
(Bragg-Reflexion) möglich ist: Die Bragg-Bedingung 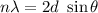 ist nur erfüllbar,
wenn die Wellenlänge kleiner ist als der doppelte Netzebenenabstand
ist nur erfüllbar,
wenn die Wellenlänge kleiner ist als der doppelte Netzebenenabstand  , welcher von
der Grössenordnung der Atom- bzw. Moleküldurchmesser ist. Eine nähere Betrachtung
des Beugungsproblems, die auch die thermische Bewegung (Gitterschwingungen)
einschliesst zeigt, dass es bei Strukturbestimmungen von Vorteil ist, wenn die
Wellenlänge nicht sehr klein ist im Vergleich zu den Abständen der Netzebenen. Die
sogenannten thermischen Neutronen aus einem Kernreaktor erfüllen diese Bedingung. Im
Moderator5
des Reaktors, der aus Graphit oder (schwerem) Wasser besteht, werden die schnellen
Neutronen, die in den Brennstoffelementen durch Kernspaltung entstehen, auf thermische
Geschwindigkeiten6
gebracht. Bei Temperaturen von einigen 100 K erhalten wir mit Hilfe der
Energieerhaltung aus dem Äquipartitionsprinzip
, welcher von
der Grössenordnung der Atom- bzw. Moleküldurchmesser ist. Eine nähere Betrachtung
des Beugungsproblems, die auch die thermische Bewegung (Gitterschwingungen)
einschliesst zeigt, dass es bei Strukturbestimmungen von Vorteil ist, wenn die
Wellenlänge nicht sehr klein ist im Vergleich zu den Abständen der Netzebenen. Die
sogenannten thermischen Neutronen aus einem Kernreaktor erfüllen diese Bedingung. Im
Moderator5
des Reaktors, der aus Graphit oder (schwerem) Wasser besteht, werden die schnellen
Neutronen, die in den Brennstoffelementen durch Kernspaltung entstehen, auf thermische
Geschwindigkeiten6
gebracht. Bei Temperaturen von einigen 100 K erhalten wir mit Hilfe der
Energieerhaltung aus dem Äquipartitionsprinzip 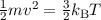 eine de
Broglie-Wellenlänge von
eine de
Broglie-Wellenlänge von
Dies entspricht etwa einem Drittel typischer Atomabstände in Kristallen oder Flüssigkeiten.
Wir haben an einigen Beispielen gesehen, dass nicht nur Photonen Wellen- und Teilcheneigenschaften zeigen, sondern auch massebehaftete Teilchen, wie Elektronen und Neutronen. Für die Entdeckung des Elektrons als Teilchen erhielt Joseph John Thomson 1906 den Nobelpreis. Sein Sohn, Georg Paget Thomson, wurde (zusammen mit Davisson) im Jahre 1937 für den Nachweis, dass Elektronen ebenfalls Welleneigenschaften zeigen, mit dem Nobelpreis geehrt.
Wir haben im letzten Abschnitt die Beugung von Materiewellen an natürlichen Kristallgittern untersucht. Man kann Materiewellen (Elektronenstrahlen) aber auch an feinen, künstlich hergestellten Gittern und Spalten beugen.
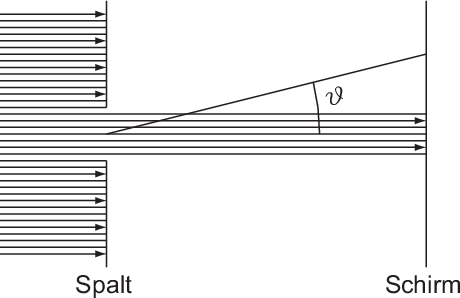
Wir untersuchen dazu folgendes Gedankenexperiment. Wir betrachten einen
Spalt, der nach klassischen Vorstellungen ideal sein soll, d.h. er soll Teilchen,
die von links (senkrecht) auf die Spaltebene einfallen, ungestört passieren
lassen. Nach der klassischen Mechanik wird ein Detektor auf der rechten
Seite des Spaltes nur geradeauslaufende Teilchen messen (siehe Abb. 6.4):
Die Teilchenhäufigkeit ist nur beim Winkel 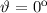 von null verschieden.
von null verschieden.
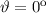 Teilchen auf dem Schirm registriert.
Teilchen auf dem Schirm registriert.Wie würde man diesen Sachverhalt mit dem Wellenbild interpretieren? Wir wissen,
dass die Teilchenhäufigkeit 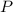 proportional zur Amplitude der gebeugten
Materiewelle ist
proportional zur Amplitude der gebeugten
Materiewelle ist
wobei  die Spaltbreite ist (siehe Abb. 6.5).
die Spaltbreite ist (siehe Abb. 6.5).
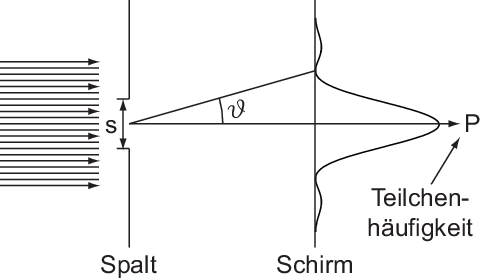
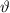 registriert.
registriert.Damit diese Häufigkeit bei 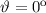 zusammengedrängt wird, muss
zusammengedrängt wird, muss 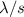 gegen
null streben. Bei endlicher Spaltbreite muss also die de Broglie-Wellenlänge
gegen
null streben. Bei endlicher Spaltbreite muss also die de Broglie-Wellenlänge
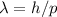 gegen null streben, damit die nach der klassischen Mechanik erwartete
Winkelverteilung resultiert. Mit
gegen null streben, damit die nach der klassischen Mechanik erwartete
Winkelverteilung resultiert. Mit
bedeutet dies, dass die Masse 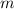 gross sein muss. Praktisch heisst das, dass sich
makroskopische Körper nach den Gesetzten der klassischen Mechanik bewegen und
erst bei kleinen Massen die Welleneigenschaften der Materieteilchen zum tragen
kommen. Wir verdeutlichen dies an zwei Beispielen.
gross sein muss. Praktisch heisst das, dass sich
makroskopische Körper nach den Gesetzten der klassischen Mechanik bewegen und
erst bei kleinen Massen die Welleneigenschaften der Materieteilchen zum tragen
kommen. Wir verdeutlichen dies an zwei Beispielen.
Mit 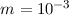 kg,
kg, 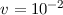 m/s und
m/s und 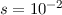 m ergibt sich für die
Winkelbreite
m ergibt sich für die
Winkelbreite 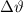 des Hauptmaximums (Abstand zwischen den beiden ersten
Minima)
des Hauptmaximums (Abstand zwischen den beiden ersten
Minima)
Wir erhalten also einen vernachlässigbar kleinen Wert.
Wir betrachten Elektronen mit einer Energie von 54 eV, die einen Spalt
passieren, dessen Breite von der Grössenordnung 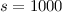 Å ist. Die de
Broglie-Wellenlänge beträgt nach (6.7)
Å ist. Die de
Broglie-Wellenlänge beträgt nach (6.7) 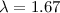 Å , sodass wir folgende
Winkelbreite
Å , sodass wir folgende
Winkelbreite 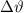 des Hauptmaximums erhalten
des Hauptmaximums erhalten
Die Welleneigenschaften kommen also zum tragen: Obwohl alle Teilchen auf der linken Seite des Spalts gleich präpariert wurden, laufen sie auf der rechten Seite unter (messbar) verschiedenen Winkeln aus.
Betrachtet man nun einen so kleinen Teilchenstrom, dass sich zu jedem
Zeitpunkt nur ein einziges Teilchen in der Apparatur aufhält, dann findet man
(nach genügend langer Zeit) dieselbe Winkelverteilung 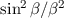 wie im
Fall eines starken Teilchenstroms, wo sich gleichzeitig viele Teilchen
in der Apparatur befinden. Die Winkelverteilung kommt also nicht
ausschliesslich durch Interferenz zwischen verschiedenen Teilchen zustande,
sondern:
wie im
Fall eines starken Teilchenstroms, wo sich gleichzeitig viele Teilchen
in der Apparatur befinden. Die Winkelverteilung kommt also nicht
ausschliesslich durch Interferenz zwischen verschiedenen Teilchen zustande,
sondern:
Die Materiewelle gibt auch bei einem einzelnen Teilchen die richtige Aufenthaltswahrscheinlichkeit und darf somit auch zur Beschreibung eines Einteilchensystems benützt werden.
Wir haben bereits erkannt, dass Materie Welleneigenschaften zeigen kann und sich diese auch experimentell beobachten lassen. Zusätzlich wissen wir aus dem letzten Abschnitt unter welchen Bedingungen dieser Wellencharakter beobachtbar wird. Wir formulieren nun als nächstes eine solche Welle, die sogenannte de Broglie-Welle, mathematisch als sogenannte Wellenfunktion.
Als Ansatz für eine ebene harmonische Materiewelle 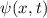 , die sich längs der
x-Achse fortpflanzt, schreiben wir
, die sich längs der
x-Achse fortpflanzt, schreiben wir
mit der Wellenzahl 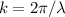 und der Amplitude der Welle
und der Amplitude der Welle 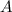 . Mit der de
Broglie-Beziehung
. Mit der de
Broglie-Beziehung 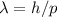 und mit
und mit 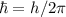 erhalten wir
erhalten wir 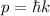 . Da sowohl
. Da sowohl 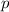 als auch
als auch 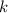 Vektoren sind, können wir auch schreiben
Vektoren sind, können wir auch schreiben
Dies ist eine andere Schreibweise der de Broglie-Beziehung. Damit ergibt sich für die ebene harmonische Materiewelle
Es ist zu bemerken, dass wir die Welle als komplexe Funktion schreiben. Dabei
entspricht der Funktion 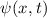 keine direkte physikalische Messgrösse. Daher
kann diese sehr wohl komplexe Werte annehmen. Hingegen sind messbare
Grössen, wie z.B. die Aufenthaltswahrscheinlichkeit (Teilchenhäufigkeit),
reell.
keine direkte physikalische Messgrösse. Daher
kann diese sehr wohl komplexe Werte annehmen. Hingegen sind messbare
Grössen, wie z.B. die Aufenthaltswahrscheinlichkeit (Teilchenhäufigkeit),
reell.
Ausgehend vom Wissen, dass die Aufenthaltswahrscheinlichkeit materieller Teilchen proportional zum Quadrat der Amplitude der Materiewelle ist, postulieren wir:
Die Wahrscheinlichkeit, ein Teilchen am Ort  zur Zeit
zur Zeit 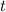 anzutreffen, ist
proportional zu
anzutreffen, ist
proportional zu 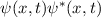 , d.h. zum Quadrat des absoluten Betrags der
Wellenfunktion
, d.h. zum Quadrat des absoluten Betrags der
Wellenfunktion 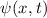 .
.
In den folgenden Kapiteln werden wir uns noch detaillierter mit diesem Postulat auseinandersetzen.
Nachdem wir nun eine Form für die ebene harmonische Materiewelle gefunden haben
und auch deren Definition, stellt sich noch die Frage, welche physikalische Grösse für
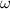 zu verwenden ist. Es ist naheliegend, die für Photonen gültige Beziehung
zu verwenden ist. Es ist naheliegend, die für Photonen gültige Beziehung
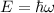 auf die Materiewellen anzuwenden, analog wie die Beziehung
auf die Materiewellen anzuwenden, analog wie die Beziehung 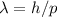 von
den Photonen übernommen wurde. Wir schreiben also für die totale Energie
eines Materieteilchens
von
den Photonen übernommen wurde. Wir schreiben also für die totale Energie
eines Materieteilchens 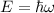 , wobei
, wobei 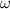 die Frequenz der de Broglie-Welle
ist.
die Frequenz der de Broglie-Welle
ist.
Damit kann die ebene harmonische Materiewelle, die de Broglie-Welle, wie folgt geschrieben werden
Gehen wir von einer ebenen harmonischen Materiewelle 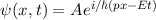 aus,
die wir im letzten Abschnitt kennengelernt haben und berechnen die entsprechende
Aufenthaltswahrscheinlichkeit, so erhalten wir den folgenden konstanten
Wert
aus,
die wir im letzten Abschnitt kennengelernt haben und berechnen die entsprechende
Aufenthaltswahrscheinlichkeit, so erhalten wir den folgenden konstanten
Wert 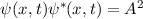 . Das bedeutet, dass die ebene harmonische Welle
ein Teilchen beschreibt, dessen Aufenthaltswahrscheinlichkeit entlang der
gesamten x-Achse konstant ist. Daher kann man einem durch eine solche
Wellenfunktion beschriebenen Teilchen keine eindeutige Position im Raum
zuweisen.
. Das bedeutet, dass die ebene harmonische Welle
ein Teilchen beschreibt, dessen Aufenthaltswahrscheinlichkeit entlang der
gesamten x-Achse konstant ist. Daher kann man einem durch eine solche
Wellenfunktion beschriebenen Teilchen keine eindeutige Position im Raum
zuweisen.
Um nun ein Teilchen zu beschreiben, dessen Aufenthaltswahrscheinlichkeit in einem bestimmten Bereich des Raums gross ist, verwendet man eine Superposition (Überlagerung) von harmonischen Wellen verschiedener Frequenzen. Die Überlagerung sollte so beschaffen sein, dass sich dabei eine Wellengruppe ausbildet (siehe Abb. 6.6). In der Quantenmechanik spricht man auch von einem Wellenpaket. Ein Wellenpaket ist also eine Welle, deren Amplitude nur in einem begrenzten Raumgebiet ungleich Null ist und deshalb ein Teilchen beschreibt, dessen Aufenthaltsbereich auf dieses Raumgebiet beschränkt ist.
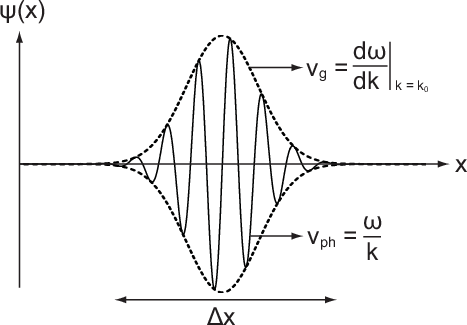
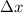 aufhält. Auf die Bedeutung der Gruppengeschwindigkeit
aufhält. Auf die Bedeutung der Gruppengeschwindigkeit 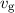 und Phasengeschwindigkeit
und Phasengeschwindigkeit 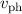 wird im Text eingegangen.
wird im Text eingegangen.Ein ähnlicher Zusammenhang ist bekannt aus der Beschreibung von elektromagnetischen Wellen. Bei ebenen Wellen ist die Intensität der Welle über den ganzen Raum gleichmässig verteilt. Um im Raum lokalisierte elektromagnetische Pulse zu beschreiben, betrachtet man Überlagerungen von Wellen verschiedener Frequenzen.
Als nächstes widmen wir uns der Frage, mit welcher Geschwindigkeit sich ein
Teilchen fortbewegt, welches durch ein Wellenpaket beschrieben ist. Da die
Aufenthaltswahrscheinlichkeit des betrachteten Teilchens nur innerhalb der
Wellengruppe gross ist, interpretiert man die Gruppengeschwindigkeit 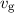 , d.h. die
Geschwindigkeit, mit der sich ein Wellenpaket als Ganzes fortbewegt, als
Geschwindigkeit des Teilchens.
, d.h. die
Geschwindigkeit, mit der sich ein Wellenpaket als Ganzes fortbewegt, als
Geschwindigkeit des Teilchens.
Die Phasengeschwindigkeit 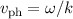 einer Materiewelle gibt an, mit welcher
Geschwindigkeit sich Stellen konstanter Phase bewegen. Sie unterscheidet sich von
der Gruppengeschwindigkeit
einer Materiewelle gibt an, mit welcher
Geschwindigkeit sich Stellen konstanter Phase bewegen. Sie unterscheidet sich von
der Gruppengeschwindigkeit 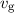 , wenn die Phasengeschwindigkeit einer Welle von
der Frequenz abhängt. Dieses Phänomen nennt man Dispersion. Die Dispersion wird
durch die Funktion
, wenn die Phasengeschwindigkeit einer Welle von
der Frequenz abhängt. Dieses Phänomen nennt man Dispersion. Die Dispersion wird
durch die Funktion 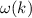 beschrieben (siehe Abb. 6.7). Ist
beschrieben (siehe Abb. 6.7). Ist 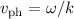 unabhängig
von
unabhängig
von 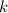 so haben wir keine Dispersion. Hängt hingegen
so haben wir keine Dispersion. Hängt hingegen 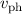 von
von 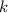 ab, so haben wir
Dispersion. Auf die genauere Bedeutung der Phasengeschwindigkeit gehen wir im
Abschnitt 6.5 ein.
ab, so haben wir
Dispersion. Auf die genauere Bedeutung der Phasengeschwindigkeit gehen wir im
Abschnitt 6.5 ein.
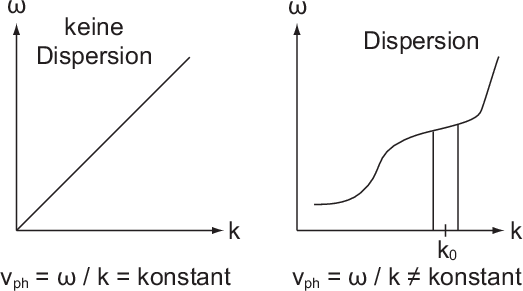
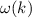 : Hängt
: Hängt 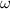 linear von
linear von 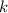 ab, so liegt keine Dispersion vor, ansonsten spricht man von
Dispersion.
ab, so liegt keine Dispersion vor, ansonsten spricht man von
Dispersion.Unser nächstes Ziel ist es einen Ausdruck für die Gruppengeschwindigkeit 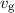 zu
definieren. Sind die
zu
definieren. Sind die 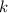 -Werte der superponierten Wellen alle in der Nähe desselben
Werts
-Werte der superponierten Wellen alle in der Nähe desselben
Werts 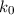 , dann ändert sich (zumindest bei stetigem Verlauf der Funktion
, dann ändert sich (zumindest bei stetigem Verlauf der Funktion 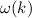 )
die Gestalt des Wellenpakets nur schwach im Laufe der Zeit (siehe Abb. 6.7). Das
Wellenpaket bewegt sich dann mit der Gruppengeschwindigkeit
)
die Gestalt des Wellenpakets nur schwach im Laufe der Zeit (siehe Abb. 6.7). Das
Wellenpaket bewegt sich dann mit der Gruppengeschwindigkeit
Jedoch muss man auch Wellenpakete in Betracht ziehen, bei denen sich die k-Werte
der superponierten Wellen über einen grösseren Bereich 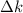 erstrecken. Das
Wellenpaket kann dann als Superposition von vielen „Subpaketen“
erstrecken. Das
Wellenpaket kann dann als Superposition von vielen „Subpaketen“  , die sich mit
der ihnen eigenen Gruppengeschwindigkeit
, die sich mit
der ihnen eigenen Gruppengeschwindigkeit 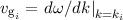 bewegen,
aufgefasst werden. Das Gesamtpaket läuft also auseinander. Wenn die Breite des
Wellenpakets bei
bewegen,
aufgefasst werden. Das Gesamtpaket läuft also auseinander. Wenn die Breite des
Wellenpakets bei 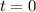
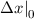 beträgt, dann wächst sie in der Zeit
beträgt, dann wächst sie in der Zeit 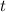 auf
auf
Immerhin kann man auch in diesem Fall einen „Schwerpunkt“ des Wellenpakets
definieren und ihm eine Gruppengeschwindigkeit 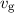 zuschreiben
zuschreiben
In diesem Abschnitt gehen wir genauer auf die Bedeutung der Phasengeschwindigkeit von Materiewellen ein und betrachten in diesem Zusammenhang das Phänomen der Brechung, welches auch aus der Optik bekannt ist.
Bei jeder (harmonischen) Welle ist die Phasengeschwindigkeit gegeben durch
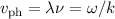 . Diese Beziehung gilt auch für Materiewellen. In diesem Fall ist
. Diese Beziehung gilt auch für Materiewellen. In diesem Fall ist
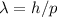 und
und 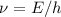 einzusetzen, so dass
einzusetzen, so dass 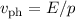 . Bezeichnen wir die
Teilchengeschwindigkeit mit
. Bezeichnen wir die
Teilchengeschwindigkeit mit  und die Ruhemasse mit
und die Ruhemasse mit  , dann gilt für ein relativistisches
Teilchen7
, dann gilt für ein relativistisches
Teilchen7
mit 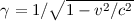 . Wir erkennen daher, dass die Phasengeschwindigkeit der
Materiewellen umgekehrt proportional zur Teilchengeschwindigkeit ist
. Wir erkennen daher, dass die Phasengeschwindigkeit der
Materiewellen umgekehrt proportional zur Teilchengeschwindigkeit ist
Da die Teilchengeschwindigkeit  die Lichtgeschwindigkeit
die Lichtgeschwindigkeit  nicht überschreiten
kann, ist die Phasengeschwindigkeit immer grösser als die Lichtgeschwindigkeit.
nicht überschreiten
kann, ist die Phasengeschwindigkeit immer grösser als die Lichtgeschwindigkeit.
Trotzdem ist die Phasengeschwindigkeit der Materiewellen nicht ganz ohne
physikalische Bedeutung. Da das Plancksche Wirkungsquantum im Ausdruck für
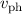 nicht vorkommt, ist zu erwarten, dass man mit der Phasengeschwindigkeit
Phänomene beschreiben kann, die auch aufgrund der klassischen Mechanik
verständlich sind. Vom Wellenstandpunkt aus müssen es Phänomene sein,
bei denen die Wellenlänge nicht eingeht, denn diese enthält das Plancksche
Wirkungsquantum. Beugungserscheinungen kommen also nicht in Frage.
Es gibt aber Wellenphänomene, die nur durch die Phasengeschwindigkeit
bestimmt sind. Ein einfaches Beispiel ist die Brechung an der Grenzfläche zweier
Gebiete mit verschiedenen Phasengeschwindigkeiten auf das wir hier kurz
eingehen.
nicht vorkommt, ist zu erwarten, dass man mit der Phasengeschwindigkeit
Phänomene beschreiben kann, die auch aufgrund der klassischen Mechanik
verständlich sind. Vom Wellenstandpunkt aus müssen es Phänomene sein,
bei denen die Wellenlänge nicht eingeht, denn diese enthält das Plancksche
Wirkungsquantum. Beugungserscheinungen kommen also nicht in Frage.
Es gibt aber Wellenphänomene, die nur durch die Phasengeschwindigkeit
bestimmt sind. Ein einfaches Beispiel ist die Brechung an der Grenzfläche zweier
Gebiete mit verschiedenen Phasengeschwindigkeiten auf das wir hier kurz
eingehen.
Das Brechungsgesetz kann mit Hilfe des Huygens-Prinzips erklärt werden. Dieses ist
ein rein kinematisches (um nicht gar zu sagen rein mathematisches) Prinzip und muss
als solches für jede Welle gelten, insbesondere auch für Materiewellen. Für eine
Grenzfläche zwischen zwei Gebieten I und II mit den Phasengeschwindigkeiten 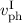 und
und  gilt allgemein (siehe Abb. 6.8)
gilt allgemein (siehe Abb. 6.8)
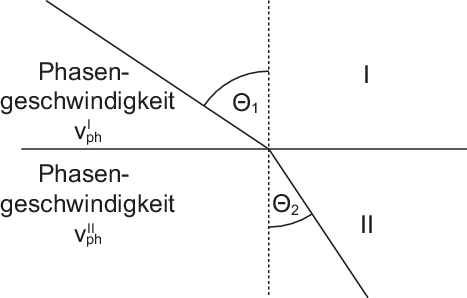
Im Fall von Schall- oder elektromagnetischen Wellen sind die Gebiete I und II verschiedene Materialien, deren physikalische Eigenschaften die Phasengeschwindigkeiten bestimmen. Für Schallwellen gilt
wobei 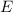 das Elastizitätsmodul und
das Elastizitätsmodul und 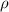 die Dichte des Materials bezeichnen. Für
elektromagnetische Wellen gilt
die Dichte des Materials bezeichnen. Für
elektromagnetische Wellen gilt
wobei  die Dielektrizitätskonstante und
die Dielektrizitätskonstante und 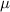 die magnetische Permeabilität des
Materials bezeichnen.
die magnetische Permeabilität des
Materials bezeichnen.
An einem einfachen Beispiel illustrieren wir nun, dass die Brechung der Materiewellen durch das Kraftfeld bestimmt ist, in welchem sich die Teilchen bewegen und dass das Brechungsgesetz die Bahn des Teilchens liefert, die es aufgrund der klassischen Mechanik durchlaufen würde. Die klassische Bahn stimmt dann mit der Erfahrung überein, wenn keine Beugung auftritt, d.h. wenn die de Broglie-Wellenlänge sehr klein ist im Vergleich zur Breite der Spalte und im Vergleich zu den Lineardimensionen der Gebiete, in welchen das Kraftfeld eine Ablenkung des Teilchens bewirkt.
Das Experiment (siehe Abb. 6.9) findet in einem evakuierten Gefäss statt, damit die
Teilchen (Elektronen) sich frei von Kollisionen ausbreiten können. Die aus
einer Glühkathode K austretenden Elektronen werden durch ein zwischen K
und A angelegtes elektrisches Feld beschleunigt und unter dem Winkel 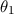 bei B in den Metallkasten I eingeschossen. Dabei ist schon bei niedrigen
Beschleunigungsspannungen
bei B in den Metallkasten I eingeschossen. Dabei ist schon bei niedrigen
Beschleunigungsspannungen 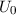 die de Broglie-Wellenlänge
die de Broglie-Wellenlänge 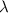 der Elektronen so
klein, dass man Beugung an den Blenden der Apparatur vernachlässigen kann. Zum
Beispiel erhalten wir für
der Elektronen so
klein, dass man Beugung an den Blenden der Apparatur vernachlässigen kann. Zum
Beispiel erhalten wir für 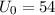 eV eine Wellenlänge von
eV eine Wellenlänge von 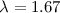 Å .
Damit ist eine klassische Berechnung der Elektronenbahn gerechtfertigt.
Å .
Damit ist eine klassische Berechnung der Elektronenbahn gerechtfertigt.
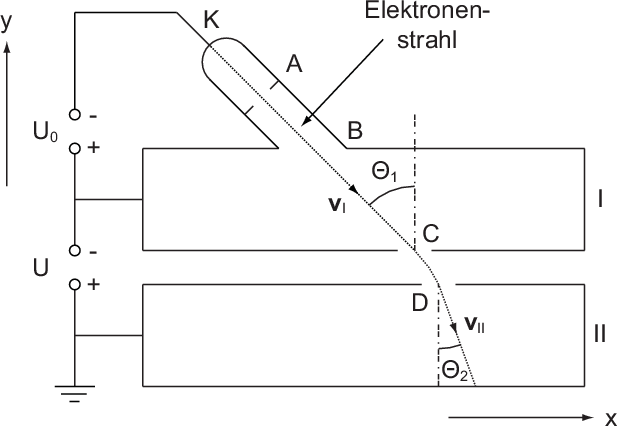
Das Potential des Kastens I gegenüber der Erde sei 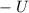 . Im Innern des Kastens I
herrscht kein elektrisches Feld, wenn wir von der sehr kleinen Ladung des
Elektronenstrahls absehen. Wir können also davon ausgehen, dass sich die Elektronen
mit einer konstanten Geschwindigkeit
. Im Innern des Kastens I
herrscht kein elektrisches Feld, wenn wir von der sehr kleinen Ladung des
Elektronenstrahls absehen. Wir können also davon ausgehen, dass sich die Elektronen
mit einer konstanten Geschwindigkeit 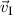 bewegen.
bewegen.
Bei C treten die Elektronen aus dem Kasten I durch ein Loch aus, um dann bei D in
den leitenden Kasten II einzutreten, der geerdet ist. In diesem Kasten bewegen sie
sich mit der konstanten Geschwindigkeit 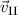 . Diese unterscheidet sich von
. Diese unterscheidet sich von 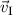 , da
zwischen den beiden Kästen durch den Potentialunterschied ein elektrisches Feld
herrscht, in welchem die Elektronen noch einmal beschleunigt werden. Dieses Feld ist
entlang der y-Achse gerichtet und beeinflusst daher nur die y-Komponente der
Geschwindigkeit. Die x-Komponente ist in beiden Kästen gleich, d.h. es
gilt
, da
zwischen den beiden Kästen durch den Potentialunterschied ein elektrisches Feld
herrscht, in welchem die Elektronen noch einmal beschleunigt werden. Dieses Feld ist
entlang der y-Achse gerichtet und beeinflusst daher nur die y-Komponente der
Geschwindigkeit. Die x-Komponente ist in beiden Kästen gleich, d.h. es
gilt
Somit erhalten wir aufgrund dieser auf der klassischen Mechanik und dem Elektromagnetismus aufbauenden Berechnung folgendes Resultat
Dasselbe Ergebnis erhalten wir, wenn wir mit de Broglie-Wellen rechnen und in das
Brechungsgesetz (6.26) für die Phasengeschwindigkeit (6.25), d.h. 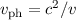 einsetzen
einsetzen
Diese Übereinstimmung ist ein Hinweis dafür, dass die de Brogliesche Wellenmechanik die klassische Mechanik als Grenzfall einschliesst, nämlich als Grenzfall vernachlässigbarer Beugung.
Die Anwendung der ursprünglich für die Photonen betrachteten Beziehungen
auf Materiewellen, was zur Form
für die de Broglie-Welle führte, war ein Schritt, den wir nun verifizieren
bzw. motivieren möchten. Wir betrachten dazu ein Teilchen, welches durch ein
Wellenpaket (superponierte de Broglie-Wellen) beschrieben wird. Wenn die de
Broglie-Wellen die Aufenthaltswahrscheinlichkeit des Teilchens liefern sollen,
muss nach Abschnitt 6.4.1 eine Gruppengeschwindigkeit 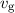 resultieren, die
gleich der klassischen Teilchengeschwindigkeit
resultieren, die
gleich der klassischen Teilchengeschwindigkeit  ist. Dies überprüfen wir
nun.
ist. Dies überprüfen wir
nun.
Aus (6.32) und (6.33) erhalten wir für die Gruppengeschwindigkeit
Wir zeigen nun, dass dieser Ausdruck sowohl für nicht-relativistische als auch für
relativistische Teilchen der Teilchengeschwindigkeit  entspricht:
entspricht:
wobei die potentielle Energie 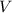 nicht vom Impuls
nicht vom Impuls 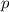 abhängen soll. Daraus
ergibt sich für die Gruppengeschwindigkeit
abhängen soll. Daraus
ergibt sich für die Gruppengeschwindigkeit
Aus (6.39) folgt
Einsetzen in (6.38) ergibt
Daraus erhalten wir für die Gruppengeschwindigkeit
D.h. sowohl relativistisch als auch nicht-relativistisch ist die Gruppengeschwindigkeit
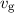 einer Materiewelle gleich der Teilchengeschwindigkeit
einer Materiewelle gleich der Teilchengeschwindigkeit  . Daher ist die
Anwendung der für die Photonen gefundenen Beziehungen (6.32) und (6.33) auf
Teilchen gerechtfertigt, d.h. die de Broglie-Wellenmechanik anwendbar.
. Daher ist die
Anwendung der für die Photonen gefundenen Beziehungen (6.32) und (6.33) auf
Teilchen gerechtfertigt, d.h. die de Broglie-Wellenmechanik anwendbar.
Hier weisen wir noch einmal auf einen wichtigen Unterschied zwischen Photonen und
Materieteilchen hin. Dazu ist es instruktiv, die Energie-Impuls-Beziehung (6.41) für
Materieteilchen mit der entsprechenden Beziehung für Photonen 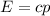 zu
vergleichen (siehe Abb. 6.10). Dabei findet man, dass das Photon einem
Teilchen im Grenzfall verschwindender Ruhemasse
zu
vergleichen (siehe Abb. 6.10). Dabei findet man, dass das Photon einem
Teilchen im Grenzfall verschwindender Ruhemasse 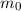 entspricht. Beim
Photon im Vakuum zeigt sich keine Dispersion und es gilt
entspricht. Beim
Photon im Vakuum zeigt sich keine Dispersion und es gilt 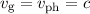 .
Daher haben Wellenpakete bei beliebigen Frequenzen im Vakuum dieselbe
Gruppengeschwindigkeit. Im Gegensatz dazu zeigt ein massebehaftetes Teilchen
Dispersion, d.h. verschiedene Frequenzkomponenten eines Wellenpakets haben
verschiedene Ausbreitungsgeschwindigkeiten.
.
Daher haben Wellenpakete bei beliebigen Frequenzen im Vakuum dieselbe
Gruppengeschwindigkeit. Im Gegensatz dazu zeigt ein massebehaftetes Teilchen
Dispersion, d.h. verschiedene Frequenzkomponenten eines Wellenpakets haben
verschiedene Ausbreitungsgeschwindigkeiten.
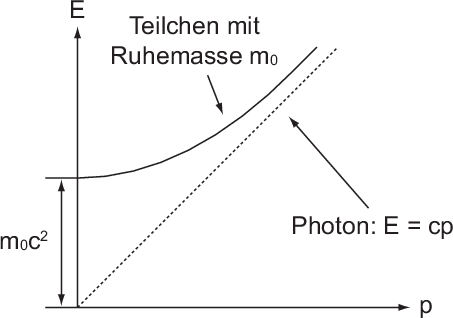
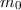 mit der entsprechenden Beziehung für Photonen.
mit der entsprechenden Beziehung für Photonen.Um diese Tatsache nochmals zu verdeutlichen, betrachten wir den nichtrelativistischen
Grenzfall (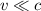 ) der Energie-Impuls-Beziehung (6.41). Wir erhalten
) der Energie-Impuls-Beziehung (6.41). Wir erhalten
wobei wir im letzten Schritt die Beziehung 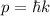 verwendet haben. Mit
verwendet haben. Mit 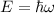 erhalten wir
erhalten wir
Somit gilt 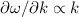 und wir haben Dispersion.
und wir haben Dispersion.
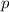 eine Materiewelle mit Wellenlänge
eine Materiewelle mit Wellenlänge
zugeordnet werden, wobei 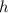 das Plancksche Wirkungsquantum ist.
das Plancksche Wirkungsquantum ist.
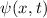 . Dieser Funktion
. Dieser Funktion 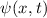 entspricht keine
direkte Messgrösse. Jedoch gilt, dass die Wahrscheinlichkeit, ein Teilchen
am Ort
entspricht keine
direkte Messgrösse. Jedoch gilt, dass die Wahrscheinlichkeit, ein Teilchen
am Ort  zur Zeit
zur Zeit 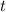 anzutreffen proportional zu
anzutreffen proportional zu 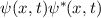 ist.
ist.
Die ebene harmonische Materiewelle, die de Broglie-Welle, ist gegeben durch
wobei 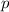 den Impuls und
den Impuls und 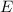 die Energie des Teilchens beschreiben.
die Energie des Teilchens beschreiben.
Ein Teilchen, dessen Aufenthaltsbereich auf ein Raumgebiet beschränkt ist,
wird durch eine Überlagerung (Superposition) von ebenen harmonischen Wellen
verschiedener Frequenz beschrieben, d.h. durch ein Wellenpaket. Die
Geschwindigkeit des Teilchens ist dabei gegeben durch die Gruppengeschwindigkeit
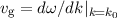 , d.h. durch die Geschwindigkeit, mit der sich das Wellenpaket
als Ganzes fortbewegt. Im Gegensatz dazu gibt die Phasengeschwindigkeit
, d.h. durch die Geschwindigkeit, mit der sich das Wellenpaket
als Ganzes fortbewegt. Im Gegensatz dazu gibt die Phasengeschwindigkeit
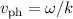 einer Materiewelle die Geschwindigkeit an, mit der sich Stellen
konstanter Phase bewegen. Hängt die Phasengeschwindigkeit von der Frequenz
ab, so spricht man von Dispersion. Bei Dispersion unterscheiden sich Phasen-
und Gruppengeschwindigkeit.
einer Materiewelle die Geschwindigkeit an, mit der sich Stellen
konstanter Phase bewegen. Hängt die Phasengeschwindigkeit von der Frequenz
ab, so spricht man von Dispersion. Bei Dispersion unterscheiden sich Phasen-
und Gruppengeschwindigkeit.
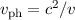 , wobei
, wobei  die
Teilchengeschwindigkeit ist. Die Phasengeschwindigkeit ist also immer grösser
als die Lichtgeschwindigkeit. Trotzdem ist sie aber nicht ganz ohne
physikalische Bedeutung. Da das Plancksche Wirkungsquantum im Ausdruck
nicht vorkommt, sind es aufgrund der klassischen Mechanik verständliche
Phänomene wie die Brechung an der Grenzfläche zweier Gebiete, die durch die
Phasengeschwindigkeit beschrieben werden können.
die
Teilchengeschwindigkeit ist. Die Phasengeschwindigkeit ist also immer grösser
als die Lichtgeschwindigkeit. Trotzdem ist sie aber nicht ganz ohne
physikalische Bedeutung. Da das Plancksche Wirkungsquantum im Ausdruck
nicht vorkommt, sind es aufgrund der klassischen Mechanik verständliche
Phänomene wie die Brechung an der Grenzfläche zweier Gebiete, die durch die
Phasengeschwindigkeit beschrieben werden können.
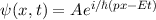 dienten die
ursprünglich für Photonen betrachteten Beziehungen
dienten die
ursprünglich für Photonen betrachteten Beziehungen 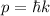 und
und
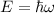 . Dieses Vorgehen wird bestätigt durch das Ergebnis, dass die
Gruppengeschwindigkeit
. Dieses Vorgehen wird bestätigt durch das Ergebnis, dass die
Gruppengeschwindigkeit 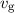 eines Wellenpakets aus superponierten de
Broglie-Wellen, welches ein nicht-relativistisches oder ein relativistisches
Teilchen beschreibt, gleich der Teilchengeschwindigkeit
eines Wellenpakets aus superponierten de
Broglie-Wellen, welches ein nicht-relativistisches oder ein relativistisches
Teilchen beschreibt, gleich der Teilchengeschwindigkeit  ist.
ist.
Obwohl Photonen und Materieteilchen viele Gemeinsamkeiten haben, gibt es doch einen wichtigen Unterschied. Das Photon entspricht einem Teilchen verschwindender Ruhemasse und zeigt daher im Vakuum keine Dispersion. Ein massebehaftetes Teilchen zeigt hingegen Dispersion, d.h. verschiedene Frequenzkomponenten eines Wellenpakets haben verschiedene Ausbreitungsgeschwindigkeiten.