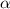 -Teilchen an Atomen
formulierte. Es dient insbesondere als Grundlage für das Bohrsche-Atommodell, das
wir in Kapitel 8 besprechen werden.
-Teilchen an Atomen
formulierte. Es dient insbesondere als Grundlage für das Bohrsche-Atommodell, das
wir in Kapitel 8 besprechen werden.
Das Wort Atom kommt aus dem Griechischen und bedeutet unteilbar. Als Atom wird
dementsprechend der kleinste unveränderliche Bestandteil eines chemischen Elements
bezeichnet. In diesem Kapitel untersuchen wir charakteristische Eigenschaften, wie
Masse und Grösse, von Atomen, betrachten die Kategorisierung der Atome im
Rahmen des Periodensystems der Elemente, beleuchten die Untersuchungsmethode
Massenspektroskopie und lernen das Rutherfordsche Atommodell kennen, welches
Ernest Rutherford aufgrund seiner Streuversuche von 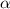 -Teilchen an Atomen
formulierte. Es dient insbesondere als Grundlage für das Bohrsche-Atommodell, das
wir in Kapitel 8 besprechen werden.
-Teilchen an Atomen
formulierte. Es dient insbesondere als Grundlage für das Bohrsche-Atommodell, das
wir in Kapitel 8 besprechen werden.
Atommassen werden in sogenannten relativen Atommassen 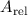 angegeben.
Experimentell hat man festgestellt, dass alle Atome eine Masse haben, die
ungefähr einem Vielfachen der Masse des Wasserstoffatoms entspricht. Deshalb
wurde eine atomare Masseneinheit 1 u eingeführt, welche ungefähr der Masse
eines Wasserstoffatoms entspricht. Dementsprechend wären zum Beispiel die
relativen Atommassen
angegeben.
Experimentell hat man festgestellt, dass alle Atome eine Masse haben, die
ungefähr einem Vielfachen der Masse des Wasserstoffatoms entspricht. Deshalb
wurde eine atomare Masseneinheit 1 u eingeführt, welche ungefähr der Masse
eines Wasserstoffatoms entspricht. Dementsprechend wären zum Beispiel die
relativen Atommassen 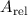 für Stickstoff (
für Stickstoff (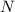 ) und Sauerstoff (
) und Sauerstoff (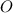 ) gegeben
durch
) gegeben
durch
Ab 1961 verwendete man aus experimentellen Gründen (präzisere Messungen von Atommassen) eine neue Definition der atomaren Masseneinheit
wobei 12 die Massenzahl 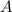 und 6 die Kernladungszahl
und 6 die Kernladungszahl 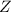 bezeichnen. Auf die
Bedeutung von Massenzahl
bezeichnen. Auf die
Bedeutung von Massenzahl 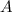 und Kernladungszahl
und Kernladungszahl 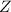 wird in Abschnitt 7.3
näher eingegangen.
wird in Abschnitt 7.3
näher eingegangen.
Den Zusammenhang zwischen den relativen und den absoluten Atommassen ergibt
sich aus dem Begriff des Mols. 1 mol ist die Stoffmenge, welche so viel Gramm wiegt,
wie das relative Atomgewicht 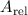 angibt. Demzufolge ergibt sich zum Beispiel für
die Masse von 1 mol Kohlenstoff
angibt. Demzufolge ergibt sich zum Beispiel für
die Masse von 1 mol Kohlenstoff 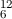 C 12 g. Nach Lorenzo Avogadro ist die Zahl der
Atome oder Moleküle einer Substanz, welche in 1 mol enthalten sind immer gleich.
Die Zahl wird mit
C 12 g. Nach Lorenzo Avogadro ist die Zahl der
Atome oder Moleküle einer Substanz, welche in 1 mol enthalten sind immer gleich.
Die Zahl wird mit 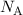 bezeichnet und heisst Avogadro-Konstante. Entsprechend der
Definition für die atomare Masseneinheit 1 u, wird die Avogadro-Konstante
bezeichnet und heisst Avogadro-Konstante. Entsprechend der
Definition für die atomare Masseneinheit 1 u, wird die Avogadro-Konstante
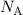 als die Anzahl Kohlenstoffatome in 12 g
als die Anzahl Kohlenstoffatome in 12 g 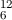 C definiert. Sie ist gegeben
durch
C definiert. Sie ist gegeben
durch
Damit ergibt sich für die absolute Atommasse 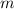 einer Substanz
einer Substanz
Wir gehen nun kurz auf einige experimentelle Methoden zur Bestimmung der Avogadro-Konstante ein:
Bei der Elektrolyse wird ein Strom durch eine Flüssigkeit geleitet. Dazu werden
zwei Elektroden (Kathode und Anode) in die Flüssigkeit eingeführt. Aufgrund
des Stroms wird an den Elektroden eine Stoffmenge abgelagert, welche
proportional zur Ladung ist, die in derselben Zeit durch die Flüssigkeit
geflossen ist. Aufgrund dieses Gesetzes (Faraday-Gesetz) lässt sich aus einer
Messung der abgeschiedenen Masse 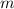 , der Stromstärke
, der Stromstärke 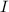 und der Zeit
und der Zeit 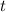 die Avogadro-Konstante
die Avogadro-Konstante 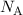 bestimmen. Für eine einwertige Substanz gilt die
Formel
bestimmen. Für eine einwertige Substanz gilt die
Formel
Zwischen der Gaskonstante 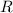 , der Boltzmann-Konstante
, der Boltzmann-Konstante 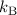 und der
Avo-gadro-Konstante
und der
Avo-gadro-Konstante 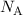 gilt der folgende Zusammenhang
gilt der folgende Zusammenhang
Demzufolge lässt sich die Avogadro-Konstante 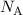 aus der Gas- und
Boltz-mann-Konstante bestimmen.
aus der Gas- und
Boltz-mann-Konstante bestimmen.
Wie in Abschnitt 3.4.2 besprochen, lässt sich mittels Röntgen-Licht bekannter
Wellenlänge die Gitterkonstante  bzw. das Volumen
bzw. das Volumen 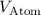 eines Atoms
bestimmen. Die Avogadro-Konstante
eines Atoms
bestimmen. Die Avogadro-Konstante 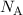 ergibt sich dann aus folgender
Formel
ergibt sich dann aus folgender
Formel
wobei 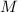 die Molmasse (entspricht bei Atomen dem relativen Atomgewicht
die Molmasse (entspricht bei Atomen dem relativen Atomgewicht
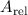 ) und
) und 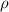 die Dichte bezeichnet.
die Dichte bezeichnet.
Für die Bestimmung der Grösse von Atomen gibt es eine Vielzahl von Möglichkeiten. Weit verbreitet sind Streuexperimente, auf die wir als erstes näher eingehen werden.
Bei einem typischen Streuexperiment (siehe Abb. 7.1) trifft ein Teilchenstrahl (aus
Atomen oder Molekülen) mit Dichte 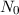 , Strahlquerschnittsfläche
, Strahlquerschnittsfläche 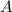 und
Teilchenradius
und
Teilchenradius 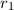 auf eine dünne Schicht der Dicke
auf eine dünne Schicht der Dicke 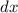 von Atomen mit Radius
von Atomen mit Radius 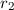 und Dichte
und Dichte 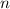 . Die Frage die nun untersucht wird ist: Wie viele Teilchen aus dem
Strahl stossen mit Atomen aus der dünnen Schicht zusammen? Oder in anderen
Worten: Welcher Anteil der Teilchen aus dem einfallenden Strahl kann die Schicht
nicht ungestört passieren?
. Die Frage die nun untersucht wird ist: Wie viele Teilchen aus dem
Strahl stossen mit Atomen aus der dünnen Schicht zusammen? Oder in anderen
Worten: Welcher Anteil der Teilchen aus dem einfallenden Strahl kann die Schicht
nicht ungestört passieren?
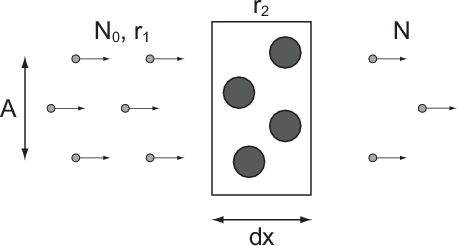
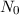 , Strahlquerschnittsfläche
, Strahlquerschnittsfläche 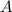 und Teilchenradius
und Teilchenradius
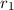 trifft auf eine dünne Schicht der Dicke
trifft auf eine dünne Schicht der Dicke 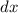 von Atomen mit Radius
von Atomen mit Radius 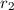 und Dichte
und Dichte 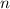 .
.Um diese Frage zu beantworten, führen wir eine neue Grösse ein, den
Wirkungsquerschnitt. Der Wirkungsquerschnitt 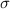 ist eine Fläche, welche
folgendermassen definiert ist: Begegnen sich einfallendes und ruhendes Teilchen
innerhalb der Fläche
ist eine Fläche, welche
folgendermassen definiert ist: Begegnen sich einfallendes und ruhendes Teilchen
innerhalb der Fläche 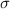 , so kommt es zum Zusammenstoss (zu einer Wechselwirkung),
ansonsten nicht. Daher ist in unserem Fall der Wirkungsquerschnitt
, so kommt es zum Zusammenstoss (zu einer Wechselwirkung),
ansonsten nicht. Daher ist in unserem Fall der Wirkungsquerschnitt 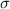 gegeben
durch (siehe Abb. 7.2)
gegeben
durch (siehe Abb. 7.2)
Mit Hilfe des Wirkungsquerschnitts können wir nun die Wahrscheinlichkeit 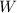 angeben, mit der ein einfallendes Teilchen innerhalb der Schicht einen Stoss erfährt.
Sie ist gegeben durch die Anzahl der Fälle in denen ein Stoss auftritt geteilt durch
die Gesamtzahl der Fälle
angeben, mit der ein einfallendes Teilchen innerhalb der Schicht einen Stoss erfährt.
Sie ist gegeben durch die Anzahl der Fälle in denen ein Stoss auftritt geteilt durch
die Gesamtzahl der Fälle
Dabei nehmen wir an, dass die Querschnittsflächen der Teilchen im durchschossenen Volumen nicht überlappen. Dies ist erfüllt, wenn die Dichte im betrachteten Volumen ausreichend gering ist.
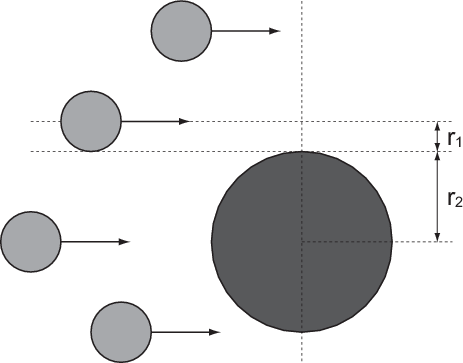
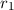 und ruhendem
Teilchen mit Radius
und ruhendem
Teilchen mit Radius 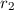 .
.Wir gehen einen Schritt weiter indem wir eine Schicht der Länge 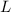 (in
Strahlrichtung) betrachten und die Anzahl der transmittierten Teilchen des
einfallenden Teilchenstrahls bestimmen. Dabei gehen wir von der zuvor betrachteten
Situation aus und zerlegen das Volumen in dünne Schichten der Dicke
(in
Strahlrichtung) betrachten und die Anzahl der transmittierten Teilchen des
einfallenden Teilchenstrahls bestimmen. Dabei gehen wir von der zuvor betrachteten
Situation aus und zerlegen das Volumen in dünne Schichten der Dicke 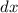 . Treten in
eine solche dünne Schicht
. Treten in
eine solche dünne Schicht 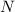 Teilchen ein, so erleidet ein Bruchteil
Teilchen ein, so erleidet ein Bruchteil 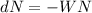 einen Stoss und wird abgelenkt. Somit erhalten wir mit (7.10) für den Anteil der in
der Schicht
einen Stoss und wird abgelenkt. Somit erhalten wir mit (7.10) für den Anteil der in
der Schicht 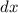 gestreuten Teilchen
gestreuten Teilchen
Den Anteil der transmittierten Atome auf der gesamten Länge 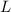 erhalten wir durch
Integration
erhalten wir durch
Integration
Für die Zahl 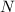 der transmittierten Teilchen ergibt sich
der transmittierten Teilchen ergibt sich
und für die Zahl der abgelenkten Teilchen erhalten wir
Das Produkt 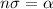 wird dabei als makroskopischer Streukoeffizient bezeichnet.
wird dabei als makroskopischer Streukoeffizient bezeichnet.
Um nun die Grösse eines Atoms zu bestimmen, geht man folgendermassen vor:
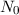 und der austretenden Teilchen
und der austretenden Teilchen 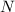 , sowie die
Teilchendichte
, sowie die
Teilchendichte 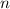 und die Länge
und die Länge 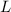 des Streukörpers.
des Streukörpers.
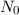 ,
, 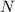 ,
, 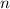 und
und 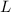 den Wirkungsquerschnitt
den Wirkungsquerschnitt 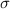 .
.
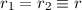 ), so ergibt sich der Atomradius
), so ergibt sich der Atomradius  und somit die Grösse
eines Atoms.
und somit die Grösse
eines Atoms.Atomgrössen werden experimentell oft nicht mittels dem Wirkungsquerschnitt
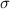 sondern mittels der mittleren freien Weglänge
sondern mittels der mittleren freien Weglänge 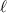 bestimmt. Diese ist
folgendermassen definiert:
bestimmt. Diese ist
folgendermassen definiert: 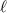 ist die Strecke, nach der nur noch ein Anteil von
ist die Strecke, nach der nur noch ein Anteil von 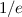 (
( ) der eintreffenden Teilchen
) der eintreffenden Teilchen 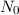 nicht gestreut worden sind, d.h. es
gilt
nicht gestreut worden sind, d.h. es
gilt
Daraus ergibt sich für die mittlere freie Weglänge 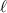 der folgende Ausdruck
der folgende Ausdruck
Unter der Annahme von 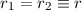 erhalten wir
erhalten wir
Würde man auch die Bewegung der gestossenen Teilchen, die wir bis jetzt vernachlässigt haben, berücksichtigen, so ändert sich die Form dieses Ausdrucks folgendermassen
Betrachtet man anstelle von Teilchen Licht, so gilt für dessen Intensität 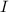 nach dem
Durchgang durch eine absorbierende Schicht der Dicke
nach dem
Durchgang durch eine absorbierende Schicht der Dicke 
Dieses Gesetz wird Beersches Gesetz genannt. Dabei entspricht 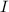 der
durchgehenden Lichtintensität,
der
durchgehenden Lichtintensität, 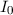 der einfallenden Lichtintensität und
der einfallenden Lichtintensität und 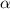 der
Absorptionskonstante der absorbierenden Schicht.
der
Absorptionskonstante der absorbierenden Schicht.
Ein reales Gas kann näherungsweise mit der Van der Waals-Gleichung1 beschrieben werden
wobei 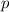 der Druck,
der Druck, 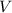 das Volumen,
das Volumen, 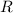 die Gaskonstante,
die Gaskonstante, 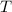 die
Temperatur und
die
Temperatur und  und
und 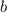 zwei Konstanten sind, welche folgende Bedeutung
haben: Aufgrund der kurzreichweitigen Abstossung zwischen den Atomen in
einem Gas steht dem Gas nur das reduzierte Volumen
zwei Konstanten sind, welche folgende Bedeutung
haben: Aufgrund der kurzreichweitigen Abstossung zwischen den Atomen in
einem Gas steht dem Gas nur das reduzierte Volumen  zur Verfügung
und wegen der langreichweitigen Abstossung ergibt sich ein zusätzlicher Druck
zur Verfügung
und wegen der langreichweitigen Abstossung ergibt sich ein zusätzlicher Druck
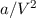 . Die Konstante
. Die Konstante 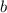 lässt sich näherungsweise aus dem
lässt sich näherungsweise aus dem 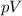 -Diagramm
bestimmen und entspricht dem vierfachen Wert des Volumens aller Atome in 1
mol
-Diagramm
bestimmen und entspricht dem vierfachen Wert des Volumens aller Atome in 1
mol
wobei 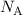 die Avogadro-Konstante ist. Daraus lässt sich das Atomvolumen
bzw. den Atomradius bestimmen.
die Avogadro-Konstante ist. Daraus lässt sich das Atomvolumen
bzw. den Atomradius bestimmen.
Der zweiten Methode sind wir schon ein paar Mal begegnet. Wie in Abschnitt 3.4.2 besprochen, lässt sich die Gitterkonstante - und damit auch eine Abschätzung der Atomgrösse - aus der Röntgen-Beugung (Bragg-Reflexion) gewinnen. Drei praktische Verfahren sind:
Bei der Besprechung einiger Abbildungstechniken soll die Frage im Zentrum
stehen, ob es möglich ist atomare Abmessungen aufzulösen, d.h. einzelne
Atome „zu sehen“. Der zentrale Begriff dabei ist das Auflösungsvermögen.
Darunter versteht man den kleinsten Abstand 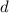 zwischen Strukturen, die
noch als getrennt abgebildet werden können. Bekannte Abbildungstechniken
sind:
zwischen Strukturen, die
noch als getrennt abgebildet werden können. Bekannte Abbildungstechniken
sind:
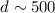 nm und für Röntgen-Strahlung eine
Auflösung von einigen 100 Å .
nm und für Röntgen-Strahlung eine
Auflösung von einigen 100 Å .
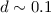 nm, was erlaubt einzelne Atome räumlich
aufzulösen.
nm, was erlaubt einzelne Atome räumlich
aufzulösen.
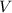 zwischen Spitze und
Oberfläche an, so ist es möglich, dass Elektronen von der Spitze auf die
Probe und umgekehrt gelangen können. Es fliesst daher ein Strom. Dieser
Effekt wird Tunneleffekt genannt und der Strom wird dementsprechend
Tunnelstrom genannt. Mit dieser Methode, die wir in einem späteren
Kapitel genauer kennen lernen werden, erhält man eine Abbildung der
elektronischen Struktur einer Oberfläche.
zwischen Spitze und
Oberfläche an, so ist es möglich, dass Elektronen von der Spitze auf die
Probe und umgekehrt gelangen können. Es fliesst daher ein Strom. Dieser
Effekt wird Tunneleffekt genannt und der Strom wird dementsprechend
Tunnelstrom genannt. Mit dieser Methode, die wir in einem späteren
Kapitel genauer kennen lernen werden, erhält man eine Abbildung der
elektronischen Struktur einer Oberfläche.
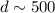 nm.
nm.In Tab. 7.1 sind die Auflösungsvermögen 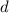 für die verschiedenen Abbildungstechniken
zusammengefasst.
für die verschiedenen Abbildungstechniken
zusammengefasst.
| Abbildungstechnik | Auflösungsvermögen 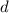 [nm] [nm] |
| Lichtmikroskop (sichtbares Licht) |  500 500 |
| Lichtmikroskop (Röntgen-Licht) | einige 10 |
| Elektronenmikroskop | 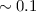 |
| Rastertunnelmikroskop (STM) |  0.1 0.1 |
| Ionenfalle |  500 500 |
Das Periodensystem der Elemente (siehe Abb. 7.3) wurde von den beiden Chemikern Dmitri Iwanowitsch Mendelejew und Lothar Meyer im Jahr 1869 unabhängig voneinander aufgestellt und ist eine Anordnung der Atome nach ihren chemischen und physikalischen Eigenschaften.
Das Periodensystem besteht aus acht vertikalen Gruppen mit Nebengruppen und sieben horizontalen Perioden. Diese Einteilung kommt aufgrund der chemischen und physikalischen Eigenschaften der Atome zustande. Sie spiegelt insbesondere den Aufbau der Atome und die dabei geltenden Gesetzmässigkeiten wider.
Die Atome werden mit einem Symbol abgekürzt, z.B. steht H für Wasserstoff, He für
Helium, ... . Die Reihenfolge und Nummerierung der Atome kommt folgendermassen
zustande: Wie wir in späteren Abschnitten sehen werden, sind Atome aus Elektronen,
Protonen und Neutronen aufgebaut. Die Protonen und Neutronen bilden den
Atomkern, der im Zentrum einer Elektronenwolke sitzt, die die Kernladung
kompensiert. Ein Atom besteht aus gleich vielen Protonen und Elektronen. Im
Periodensystem werden die Atome nun nach steigender Kernladungszahl 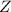 (auch
Ordnungszahl genannt) aufgeführt. Sie ist oberhalb jedes Atoms aufgeführt und
entspricht der Anzahl der Protonen und somit auch der Anzahl der Elektronen im
Atom. Unterhalb jedes Atoms ist die relative Atommasse
(auch
Ordnungszahl genannt) aufgeführt. Sie ist oberhalb jedes Atoms aufgeführt und
entspricht der Anzahl der Protonen und somit auch der Anzahl der Elektronen im
Atom. Unterhalb jedes Atoms ist die relative Atommasse 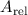 angegeben.
In diesem Zusammenhang führen wir noch den Begriff der Massenzahl
angegeben.
In diesem Zusammenhang führen wir noch den Begriff der Massenzahl 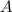 ein. Sie ist die der relativen Atommasse
ein. Sie ist die der relativen Atommasse 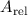 nächstgelegene ganze Zahl
und entspricht der Summe der Anzahl Protonen und Neutronen, d.h. es
gilt
nächstgelegene ganze Zahl
und entspricht der Summe der Anzahl Protonen und Neutronen, d.h. es
gilt
wobei 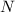 für die Anzahl der Neutronen steht.
für die Anzahl der Neutronen steht.
Zum Abschluss dieses kurzen Überblicks ein paar Bemerkungen zum Begriff der
Isotopie: Zwei Atome, welche gleiche Kernladungszahl 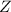 , aber unterschiedliche
Massenzahl
, aber unterschiedliche
Massenzahl 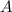 haben werden als Isotope bezeichnet. Der Unterschied in der
Massenzahl
haben werden als Isotope bezeichnet. Der Unterschied in der
Massenzahl 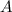 kommt durch die unterschiedliche Anzahl Neutronen
kommt durch die unterschiedliche Anzahl Neutronen 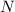 im Kern
der Atome zustande. Dieses Phänomen wurde mittels der Massenspektroskopie
entdeckt, die wir im nächsten Abschnitt besprechen werden.
im Kern
der Atome zustande. Dieses Phänomen wurde mittels der Massenspektroskopie
entdeckt, die wir im nächsten Abschnitt besprechen werden.
Die Massenspektroskopie dient zur Trennung von Atomsorten, welche unterschiedliche
Ladungs-Massenverhältnisse 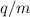 aufweisen und wie im vorangehenden
Abschnitt erwähnt, stand sie damit auch am Ursprung der Entdeckung der
Isotopie.
aufweisen und wie im vorangehenden
Abschnitt erwähnt, stand sie damit auch am Ursprung der Entdeckung der
Isotopie.
Die Parabelmethode ist eine der ersten Methoden der Massenspektroskopie.
Sie wurde 1913 von Joseph John Thomson entwickelt. Bei der verwendeten
Versuchsanordnung (siehe Abb. 7.4) wird ein Ionenstrahl bzw. ein Strahl geladener
Teilchen mit unterschiedlichen Ladungs-Massenverhältnissen 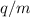 durch ein
elektrisches Feld
durch ein
elektrisches Feld 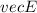 eines Kondensators und einem dazu parallelen Magnetfeld
eines Kondensators und einem dazu parallelen Magnetfeld
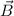 räumlich getrennt. Auf dem Beobachtungsschirm ordnen sich die Teilchen mit
gleichem Ladungs-Massenverhältnis
räumlich getrennt. Auf dem Beobachtungsschirm ordnen sich die Teilchen mit
gleichem Ladungs-Massenverhältnis 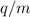 , aber unterschiedlicher Geschwindigkeit
, aber unterschiedlicher Geschwindigkeit  entlang einer Parabel an, daher auch der Name Parabelmethode. So entsteht
schlussendlich auf dem Beobachtungsschirm eine Schar unterschiedlicher Parabeln,
die jeweils einem bestimmten Ladungs-Massenverhältnis
entlang einer Parabel an, daher auch der Name Parabelmethode. So entsteht
schlussendlich auf dem Beobachtungsschirm eine Schar unterschiedlicher Parabeln,
die jeweils einem bestimmten Ladungs-Massenverhältnis 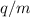 zuzuordnen sind.
zuzuordnen sind.
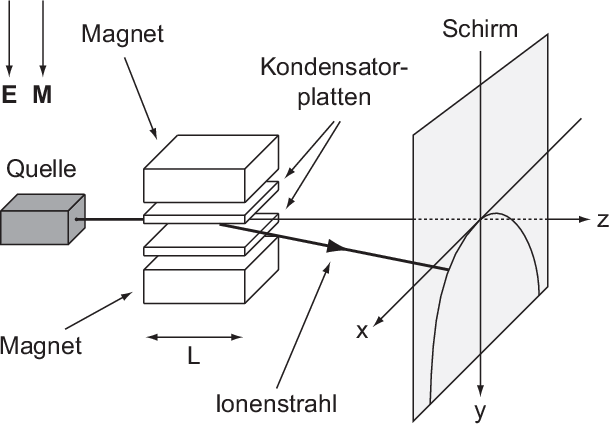
Wir geben nun eine kurze Herleitung dieses Sachverhalts, wobei wir in einem ersten
Schritt den Einfluss von elektrischem Feld 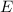 und Magnetfeld
und Magnetfeld 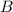 getrennt
betrachten:
getrennt
betrachten:
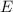 ist homogen entlang der y-Richtung. Dadurch
erfährt ein geladenes Teilchen eine Ablenkung entlang dieser Richtung. Für die
y-Koordinate
ist homogen entlang der y-Richtung. Dadurch
erfährt ein geladenes Teilchen eine Ablenkung entlang dieser Richtung. Für die
y-Koordinate 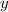 eines geladenen Teilchens der Ladung
eines geladenen Teilchens der Ladung 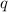 gilt die
Bewegungsgleichung
gilt die
Bewegungsgleichung Daraus folgt für die y-Koordinate
wobei wir im zweiten Schritt die Verweilzeit 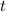 des Teilchens im Kondensator
durch seine Geschwindigkeit
des Teilchens im Kondensator
durch seine Geschwindigkeit  und die Kondensatorlänge
und die Kondensatorlänge 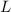 ausgedrückt
haben. Dabei haben wir angenommen, dass das Magnetfeld klein und der
Bahnradius des Teilchens gross ist.
ausgedrückt
haben. Dabei haben wir angenommen, dass das Magnetfeld klein und der
Bahnradius des Teilchens gross ist.
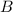 ist wie das elektrische Feld
ist wie das elektrische Feld 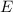 homogen entlang
der y-Richtung. Dadurch erfährt das geladen Teilchen eine Lorentz-Kraft
homogen entlang
der y-Richtung. Dadurch erfährt das geladen Teilchen eine Lorentz-Kraft 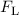 ,
welche es auf eine Kreisbahn in der Ebene senkrecht zur Feldrichtung
(xz-Ebene) zwingt. Dabei nimmt die Lorentz-Kraft
,
welche es auf eine Kreisbahn in der Ebene senkrecht zur Feldrichtung
(xz-Ebene) zwingt. Dabei nimmt die Lorentz-Kraft 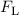 die Funktion einer
Zentripetalkraft
die Funktion einer
Zentripetalkraft 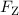 ein
ein wobei  dem Bahnradius entspricht und allgemein als Zyklotronradius
bezeichnet wird. Daraus ergibt sich für die Zentripetalbeschleunigung
dem Bahnradius entspricht und allgemein als Zyklotronradius
bezeichnet wird. Daraus ergibt sich für die Zentripetalbeschleunigung
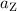
Das geladene Teilchen befindet sich nur eine relativ kurze Zeit unter dem
Einfluss des Magnetfeld und daher können wir annehmen, dass die Bewegung
entlang der x-Richtung eine gleichmässig beschleunigte Bewegung mit der
Beschleunigung 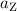 ist. In der Zeit
ist. In der Zeit 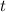 kommt es damit zu folgender Ablenkung
kommt es damit zu folgender Ablenkung
 in x-Richtung
in x-Richtung
Wiederum ersetzen wir die Verweilzeit 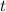 durch den Quotienten
durch den Quotienten  . Wir
erhalten mit (7.26)
. Wir
erhalten mit (7.26)
Auflösen von (7.28) nach  und einsetzen in (7.24) ergibt
und einsetzen in (7.24) ergibt
Diese Gleichung ist die Gleichung einer Parabel. Die Form hängt dabei von den
bekannten Grössen 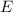 ,
, 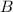 und
und 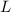 , sowie dem Ladungs-Massenverhältnis
, sowie dem Ladungs-Massenverhältnis 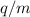 ab.
Somit ist die zu Beginn getätigte Aussage bestätigt: Auf dem Beobachtungsschirm
entsteht eine Schar unterschiedlicher Parabeln, die jeweils einem bestimmten
Ladungs-Massenverhältnis
ab.
Somit ist die zu Beginn getätigte Aussage bestätigt: Auf dem Beobachtungsschirm
entsteht eine Schar unterschiedlicher Parabeln, die jeweils einem bestimmten
Ladungs-Massenverhältnis 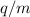 zuzuordnen sind. Damit ist wie bereits erwähnt eine
räumliche Trennung von Isotopen - oder ganz allgemein die Trennung von geladenen
Teilchen mit unterschiedlichen Ladungs-Massenverhältnissen
zuzuordnen sind. Damit ist wie bereits erwähnt eine
räumliche Trennung von Isotopen - oder ganz allgemein die Trennung von geladenen
Teilchen mit unterschiedlichen Ladungs-Massenverhältnissen 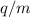 - möglich.
Zusätzlich kann bei bekannter Ladung
- möglich.
Zusätzlich kann bei bekannter Ladung 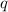 aus der Form einer Parabel die
Teilchenmasse
aus der Form einer Parabel die
Teilchenmasse 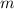 bestimmt werden.
bestimmt werden.
In den Jahren nach der Erfindung der Parabelmethode durch Joseph John Thomson wurden diverse Verbesserungen angebracht, die zu hochauflösenden Massenspektrometern führten:
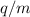 sich neu in
einem einzelnen Punkt und nicht mehr verteilt auf einer Parabel sammeln. Im
Wesentlichen werden dazu gekreuzte anstatt parallele elektrische und
magnetische Felder verwendet. Das Massenauflösungsvermögen
sich neu in
einem einzelnen Punkt und nicht mehr verteilt auf einer Parabel sammeln. Im
Wesentlichen werden dazu gekreuzte anstatt parallele elektrische und
magnetische Felder verwendet. Das Massenauflösungsvermögen 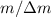 beträgt für diese Methode
beträgt für diese Methode wobei 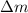 die kleinste noch unterscheidbare Massendifferenz ist.
die kleinste noch unterscheidbare Massendifferenz ist.
Neben der bereits erwähnten Verwendung in der Atomphysik zur Analyse und Trennung von Zusammensetzungen verschiedener Isotope findet die Massenspektroskopie in diversen Gebieten der Chemie und Physik ihre Anwendung:
Es sei hier noch die Bemerkung angefügt, dass zur Trennung von Zusammensetzungen verschiedener Isotope neben der Massenspektroskopie diverse andere Methoden zur Verfügung stehen und eingesetzt werden. Eine Übersicht gibt zum Beispiel das Buch Atom- und Quantenphysik von Hermann Haken und Hans Wolf [9].
Ein erster Schritt in Richtung dem Atommodell, das wir heute kennen, lieferten
Erkenntnisse aus Streuexperimenten mit Elektronen an Materie (Atomen) sowie die
durch Rutherford durchgeführten Streuexperimenten mit 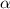 -Teilchen an
Goldfolien.
-Teilchen an
Goldfolien.
Erste Untersuchungen von Atomen durch Elektronen-Streuung gehen etwa auf das Jahr 1890 zurück. Sie wurden vom deutschen Physiker Philipp Lenard durchgeführt (siehe Abb. 7.5): (1) Mittels Thermoemission werden Elektronen erzeugt, die dann (2) beschleunigt werden und (3) mit Atomen wechselwirken. Die Elektronen, die durchgehen, werden (4) in einem Elektronen-Detektor aufgefangen und gezählt.
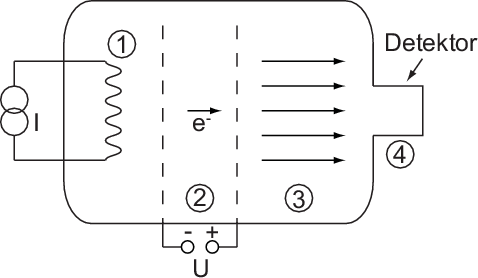
Bei der Wechselwirkung der Elektronen mit den Atomen können verschiedene Streuprozesse auftreten:
Führt man das beschriebene Experiment durch, so beobachtet man, dass bei
ausreichend hohen Beschleunigungsspannungen 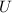 Elektronen einige cm Gas (bei
Normaldruck 1 bar) bzw. einige
Elektronen einige cm Gas (bei
Normaldruck 1 bar) bzw. einige 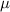 m dicke Metallplatten (
m dicke Metallplatten (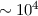 Atomlagen)
durchdringen können. Die Wechselwirkung zwischen Elektronen und Atomen ist
folglich viel kleiner als die Wechselwirkung zwischen Atomen. Insbesondere zeigt
dieses Resultat, dass Atome für Elektronen durchdringbar sind. Wäre dem nicht so,
so würde eine Streuung der Elektronen innerhalb der mittleren gaskinetischen freien
Weglänge (
Atomlagen)
durchdringen können. Die Wechselwirkung zwischen Elektronen und Atomen ist
folglich viel kleiner als die Wechselwirkung zwischen Atomen. Insbesondere zeigt
dieses Resultat, dass Atome für Elektronen durchdringbar sind. Wäre dem nicht so,
so würde eine Streuung der Elektronen innerhalb der mittleren gaskinetischen freien
Weglänge (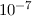 m) stattfinden.
m) stattfinden.
Wir kommen nun zur quantitativen Messung des Wirkungsquerschnitts 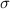 . Der
Aufbau eines möglichen Experiments entspricht im Wesentlichen dem in Abb. 7.5.
Dabei wird die einfallende und die durchgelassene Elektronen-Intensi-tät
. Der
Aufbau eines möglichen Experiments entspricht im Wesentlichen dem in Abb. 7.5.
Dabei wird die einfallende und die durchgelassene Elektronen-Intensi-tät 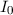 bzw.
bzw. 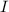 , sowie die Dichte
, sowie die Dichte 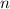 der Streuatome bestimmt. Diese Messungen erfolgen
für verschiedene Beschleunigungsspannungen
der Streuatome bestimmt. Diese Messungen erfolgen
für verschiedene Beschleunigungsspannungen 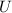 . Der Wirkungsquerschnitt
. Der Wirkungsquerschnitt 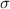 ergibt
sich aus der Formel (7.19)
ergibt
sich aus der Formel (7.19)
wobei  der Länge der Wechselwirkungszone zwischen Elektronen und Atomen und
der Länge der Wechselwirkungszone zwischen Elektronen und Atomen und
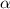 dem makroskopischer Streukoeffizient entsprechen. Unter der Annahme von
gleichen Streuatomen gilt
dem makroskopischer Streukoeffizient entsprechen. Unter der Annahme von
gleichen Streuatomen gilt
Die Summe 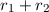 bezeichnen wir mit
bezeichnen wir mit 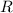 .
. 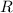 entspricht dem sogenannten
Stossradius. Das Resultat einer Messung des Stossradius
entspricht dem sogenannten
Stossradius. Das Resultat einer Messung des Stossradius 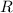 in Abhängigkeit der
Elektronengeschwindigkeit
in Abhängigkeit der
Elektronengeschwindigkeit  (siehe Abb. 7.6) zeigt, dass nur ein kleiner Bruchteil
eines Atoms für Elektronen (insbesondere schnelle Elektronen) undurchlässig ist.
Nach Lenard ist das Innere eines Atoms so leer wie das Weltall. Daraus wurde
geschlossen, dass Masse und Ladung ungleichmässig (körnig) im Atom verteilt sind.
(siehe Abb. 7.6) zeigt, dass nur ein kleiner Bruchteil
eines Atoms für Elektronen (insbesondere schnelle Elektronen) undurchlässig ist.
Nach Lenard ist das Innere eines Atoms so leer wie das Weltall. Daraus wurde
geschlossen, dass Masse und Ladung ungleichmässig (körnig) im Atom verteilt sind.
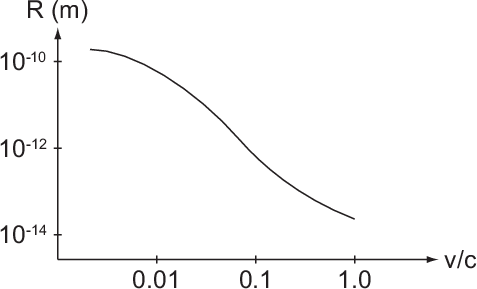
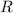 in Abhängigkeit der Elektronengeschwindigkeit
in Abhängigkeit der Elektronengeschwindigkeit  (ausgedrückt in Einheiten der Lichtgeschwindigkeit
(ausgedrückt in Einheiten der Lichtgeschwindigkeit  ).
).Die Vorstellung eines Atomkerns, der die gesamte positive Ladung und beinahe die gesamte Masse des Atoms enthält, entstand durch die Versuche von Rutherford mit denen wir uns im nächsten Abschnitt beschäftigen.
Rutherford untersuchte in seinen Versuchen nicht die Streuung von Elektronen, sondern
die Streuung von 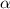 -Teilchen an einer Folie.
-Teilchen an einer Folie. 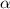 -Teilchen sind doppelt ionisierte
Helium-Kerne
-Teilchen sind doppelt ionisierte
Helium-Kerne 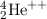 mit einer hohen kinetischen Energie
mit einer hohen kinetischen Energie 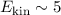 MeV. Sie
entstehen bei einem radioaktiven Zerfall. Für
MeV. Sie
entstehen bei einem radioaktiven Zerfall. Für 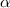 -Teilchen ist es möglich viele
Atomschichten zu passieren bis sie alle ihre kinetische Energie an die Atome
abgegeben haben. Z.B. kommen
-Teilchen ist es möglich viele
Atomschichten zu passieren bis sie alle ihre kinetische Energie an die Atome
abgegeben haben. Z.B. kommen 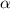 -Teilchen in Luft unter Normalbedingungen erst
nach einer Strecke von 3.5 cm zum Stillstand.
-Teilchen in Luft unter Normalbedingungen erst
nach einer Strecke von 3.5 cm zum Stillstand.
Beim Rutherford-Streuexperiment (siehe Abb. 7.7) werden 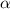 -Teilchen durch den
Zerfall eines radioaktiven Materials erzeugt. Der Strahl wird durch einen Kollimator
gebündelt und trifft auf eine Metallfolie. Als Detektor dient ein Szintillationsschirm,
welcher durch die
-Teilchen durch den
Zerfall eines radioaktiven Materials erzeugt. Der Strahl wird durch einen Kollimator
gebündelt und trifft auf eine Metallfolie. Als Detektor dient ein Szintillationsschirm,
welcher durch die 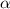 -Teilchen angeregt wird und Licht ausstrahlt, welches
beobachtet werden kann.
-Teilchen angeregt wird und Licht ausstrahlt, welches
beobachtet werden kann.
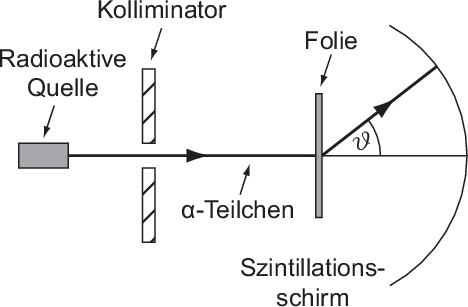
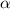 -Teilchen werden an einer Folie gestreut und
anschliessend auf einem Szintillationsschirm registriert.
-Teilchen werden an einer Folie gestreut und
anschliessend auf einem Szintillationsschirm registriert.In diesem Experiment interessiert uns nicht wie bisher die ungestört durchgelassen
Intensität der 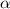 -Teilchen, sondern die Intensität der gestreuten
-Teilchen, sondern die Intensität der gestreuten 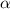 -Teilchen in
Abhängigkeit des Streuwinkels
-Teilchen in
Abhängigkeit des Streuwinkels 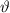 . Die Messung liefert folgendes Ergebnis:
. Die Messung liefert folgendes Ergebnis:
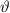 .
.
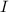
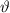 vor.
vor.Rutherford deutete diese Resultate wie folgt (siehe Abb. 7.8): Rutherfordsches Atommodell (1911)
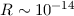 m, welcher beinahe
die gesamte Masse des Atoms enthält. Die Streuung von
m, welcher beinahe
die gesamte Masse des Atoms enthält. Die Streuung von 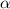 -Teilchen
erfolgt fast ausschliesslich an diesen Kernen.
-Teilchen
erfolgt fast ausschliesslich an diesen Kernen.
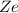 . Dabei bezeichnet
. Dabei bezeichnet
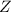 die Kernladungszahl.
die Kernladungszahl.
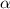 -Teilchen und Atomkern ist rein
elektrostatisch und durch die Coulomb-Wechselwirkung bestimmt.
-Teilchen und Atomkern ist rein
elektrostatisch und durch die Coulomb-Wechselwirkung bestimmt.Wir kommen nun zurück zum ursprünglichen Streuexperiment und leiten eine Formel
für die Streuintensität in Abhängigkeit des Streuwinkels 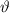 her. Wir betrachten die
Streuung von
her. Wir betrachten die
Streuung von 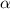 -Teilchen an einem Atomkern der Ladung
-Teilchen an einem Atomkern der Ladung 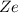 (siehe Abb. 7.9).
(siehe Abb. 7.9).
Es gelten die folgenden Annahmen:
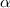 -Teilchen und der Atomkern sind punktförmig.
-Teilchen und der Atomkern sind punktförmig.
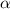 -Teilchen.
-Teilchen.
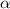 -Teilchen nicht abgelenkt, so würden sie in einem Abstand
-Teilchen nicht abgelenkt, so würden sie in einem Abstand
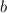 am Kern vorbeifliegen.
am Kern vorbeifliegen. 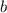 wird Stossparameter genannt.
wird Stossparameter genannt.
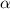 -Teilchen und Atomkern rein elektrostatisch und durch die
Coulomb-Wechselwirkung bestimmt. Die Coulomb-Kraft
-Teilchen und Atomkern rein elektrostatisch und durch die
Coulomb-Wechselwirkung bestimmt. Die Coulomb-Kraft 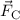 zwischen einem
zwischen einem
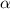 -Teilchen der Ladung
-Teilchen der Ladung 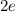 und dem Atomkern der Ladung
und dem Atomkern der Ladung 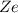 ist gegeben
durch
ist gegeben
durch wobei  der Abstand zwischen
der Abstand zwischen 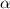 -Teilchen und Kern bezeichnet.
-Teilchen und Kern bezeichnet.
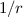 -Zentralpotenzial als mögliche
Bahnkurven Ellipsen, Hyperbeln oder Parabeln zulässt. Da die Coulomb-Kraft
eine abstossende Wirkung hat, kommen als mögliche Bahnkurven jedoch nur
Hyperbeln mit dem Atomkern im Brennpunkt in Frage.
-Zentralpotenzial als mögliche
Bahnkurven Ellipsen, Hyperbeln oder Parabeln zulässt. Da die Coulomb-Kraft
eine abstossende Wirkung hat, kommen als mögliche Bahnkurven jedoch nur
Hyperbeln mit dem Atomkern im Brennpunkt in Frage.Die Vorgehensweise ist nun die folgende:
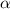 -Teilchens an einem einzelnen Atomkern und berechnen den
Zusammenhang zwischen Stossparameter
-Teilchens an einem einzelnen Atomkern und berechnen den
Zusammenhang zwischen Stossparameter 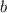 und Streuwinkel
und Streuwinkel 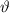 .
.
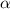 -Teilchens an einem einzelnen Atomkern zu betrachten. Wir erweitern
daher in einem zweiten Schritt das Modell auf
-Teilchens an einem einzelnen Atomkern zu betrachten. Wir erweitern
daher in einem zweiten Schritt das Modell auf 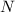
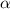 -Teilchen, welche an
einer Folie (Dicke
-Teilchen, welche an
einer Folie (Dicke 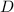 , Fläche
, Fläche 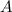 und Dichte
und Dichte 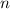 ) streuen und bestimmen
die Zahl
) streuen und bestimmen
die Zahl 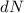 der Teilchen welche vom Detektor bei einem bestimmten
Streuwinkel
der Teilchen welche vom Detektor bei einem bestimmten
Streuwinkel 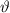 registriert werden.
registriert werden.Wir kommen zur Herleitung nach der oben aufgeführten Vorgehensweise:
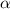 -Teilchens im Punkt A sei
-Teilchens im Punkt A sei 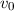 . Wie bereits
erwähnt bewegt sich das
. Wie bereits
erwähnt bewegt sich das 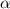 -Teilchen entlang einer Hyperbel. Wir betrachten
nun das
-Teilchen entlang einer Hyperbel. Wir betrachten
nun das 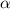 -Teilchen in einem beliebiger Punkt B mit den Polarkoordinaten
(
-Teilchen in einem beliebiger Punkt B mit den Polarkoordinaten
( ,
, 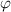 ) auf dieser Hyperbel und zerlegen die dort wirkende Kraft
) auf dieser Hyperbel und zerlegen die dort wirkende Kraft  in eine
senkrechte und eine horizontale Komponente
in eine
senkrechte und eine horizontale Komponente 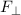 bzw.
bzw. 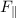 , d.h. es gilt
, d.h. es gilt
Entlang der Hyperbel sind Kraft 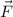 und Abstandsvektor
und Abstandsvektor 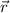 immer parallel
zueinander. Demzufolge verschwindet das Drehmoment
immer parallel
zueinander. Demzufolge verschwindet das Drehmoment 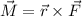 und der
Bahndrehimpuls
und der
Bahndrehimpuls 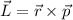 ist entlang der Hyperbel erhalten. Insbesondere
können wir den Bahndrehimpuls in Punkt A mit demjenigen in Punkt B
gleichsetzen
ist entlang der Hyperbel erhalten. Insbesondere
können wir den Bahndrehimpuls in Punkt A mit demjenigen in Punkt B
gleichsetzen
Wir stellen nun die Bewegungsgleichung für die Bewegung senkrecht zur ursprünglichen Flugrichtung auf
Integration über die Zeit von Punkt A nach C und ersetzen von 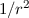 mit Hilfe
von (7.38) liefert
mit Hilfe
von (7.38) liefert
Wir substituieren auf der linken Seite 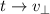 und auf der rechten Seite
und auf der rechten Seite
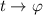 und erhalten
und erhalten
Zur Auswertung des Integrals betrachten wir die Grenzen etwas genauer. Wir
nehmen an, dass der Punkt A soweit vom Kern entfernt ist (im Unendlichen),
dass keine Coulomb-Kraft wirkt und daher 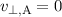 ist. Ausserdem gilt:
ist. Ausserdem gilt:
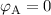 . Auch den Punkt C schieben wir ins Unendliche, sodass gilt
. Auch den Punkt C schieben wir ins Unendliche, sodass gilt
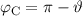 . Die Geschwindigkeit entspricht aufgrund der Energieerhaltung
derjenigen Geschwindigkeit im Punkt A. Folglich gilt
. Die Geschwindigkeit entspricht aufgrund der Energieerhaltung
derjenigen Geschwindigkeit im Punkt A. Folglich gilt 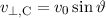 .
Einsetzen der Grenzen in (7.41) liefert
.
Einsetzen der Grenzen in (7.41) liefert
Somit erhalten wir
Mit 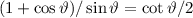 erhalten wir schlussendlich für den
Stossparameter
erhalten wir schlussendlich für den
Stossparameter 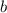 in Abhängigkeit des Streuwinkels
in Abhängigkeit des Streuwinkels 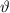 den folgenden
Ausdruck
den folgenden
Ausdruck
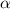 -Teilchen bei einem festen Winkel
-Teilchen bei einem festen Winkel 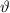 zu messen, sondern
nur in einem Winkelintervall [
zu messen, sondern
nur in einem Winkelintervall [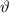 ,
, 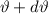 ] (siehe Abb. 7.10). Die
entsprechenden Stossparameter liegen im Intervall [
] (siehe Abb. 7.10). Die
entsprechenden Stossparameter liegen im Intervall [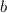 ,
, 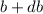 ].
]. Aus (7.44) folgt folgender Zusammenhang
Wir sehen, dass mit wachsendem Stossparameter 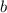 der Streuwinkel
der Streuwinkel 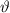 kleiner
wird. D.h.
kleiner
wird. D.h. 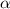 -Teilchen mit einem Stossparameter
-Teilchen mit einem Stossparameter 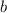 im Intervall [
im Intervall [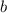 ,
,
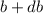 ] werden in das Winkelintervall [
] werden in das Winkelintervall [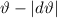 ,
, 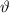 ] gestreut. Dabei
gilt
] gestreut. Dabei
gilt
Da unser Problem rotationssymmetrisch ist, entspricht einem Streuwinkelintervall
[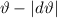 ,
, 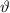 ] ein ganzer Kreisring. Entsprechend stammen die zugehörigen
Stossparameter auch aus einem Kreisring der Radien
] ein ganzer Kreisring. Entsprechend stammen die zugehörigen
Stossparameter auch aus einem Kreisring der Radien 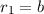 und
und 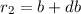 ,
siehe Abb. 7.10. Diese Stossparameter stammen aus einer Fläche
,
siehe Abb. 7.10. Diese Stossparameter stammen aus einer Fläche 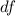 , der
sogenannten aktiven Fläche für dieses Streuwinkelintervall [
, der
sogenannten aktiven Fläche für dieses Streuwinkelintervall [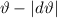 ,
, 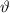 ]. Es
gilt
]. Es
gilt
Bisher haben wir nur ein Streuatom der Folie betrachtet. Wir erweitern nun
das Modell indem wir uns die gesamte Folie (Dicke 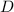 , Fläche
, Fläche 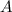 und Dichte
und Dichte  ) anschauen. Für die aktive Fläche
) anschauen. Für die aktive Fläche 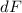 aller Atome
gilt
aller Atome
gilt
Dabei haben wir angenommen, dass sich die aktiven Flächen der einzelnen Streuatome nicht überlappen. Diese Annahme ist bei dünnen Folien (bis 10000 Atomlagen) gerechtfertigt.
Die Wahrscheinlichkeit 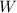 , dass ein
, dass ein 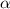 -Teilchen die aktiven Flächen
-Teilchen die aktiven Flächen 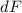 der
Folienatome trifft, beträgt
der
Folienatome trifft, beträgt
Mit anderen Worten: 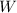 ist die Wahrscheinlichkeit, dass ein einfallendes
ist die Wahrscheinlichkeit, dass ein einfallendes
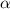 -Teilchen ins Winkelintervall [
-Teilchen ins Winkelintervall [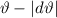 ,
, 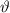 ] gestreut wird. Nun erweitern
wir das Modell von einem auf
] gestreut wird. Nun erweitern
wir das Modell von einem auf 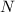 einfallende
einfallende 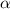 -Teilchen. Dann ist die Anzahl
-Teilchen. Dann ist die Anzahl
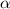 -Teilchen
-Teilchen 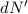 , welche in das Winkelintervall [
, welche in das Winkelintervall [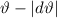 ,
, 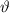 ] gestreut
werden, gegeben durch
] gestreut
werden, gegeben durch
Ein Detektor misst schlussendlich nicht die Anzahl einfallender 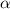 -Teilchen
-Teilchen
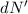 auf einem ganzen Kreisring, sondern die Anzahl einfallender
auf einem ganzen Kreisring, sondern die Anzahl einfallender
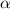 -Teil-chen
-Teil-chen 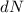 innerhalb eines kleinen Segments. Wir betrachten
das Ganze auf der Einheitskugel: Sei
innerhalb eines kleinen Segments. Wir betrachten
das Ganze auf der Einheitskugel: Sei 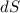 die Fläche des Kreisrings
und
die Fläche des Kreisrings
und 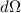 die Fläche des Segments (auch Raumwinkel genannt), dann
gilt
die Fläche des Segments (auch Raumwinkel genannt), dann
gilt
Die Fläche 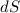 des Kreisrings beträgt
des Kreisrings beträgt
Einsetzen von (7.50) und (7.52) in (7.51) ergibt
Mit (7.44), (7.45) und (7.46) erhalten wir für das Verhältnis 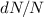 , d.h. für
die Anzahl in ein Raumwinkelelement
, d.h. für
die Anzahl in ein Raumwinkelelement 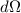 um den Streuwinkel
um den Streuwinkel 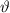 gestreuter
gestreuter
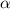 -Teilchen
-Teilchen 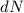 durch die Anzahl der einfallenden
durch die Anzahl der einfallenden 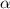 -Teilchen
-Teilchen 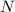 , das
folgende Schlussresultat:
, das
folgende Schlussresultat:
Rutherfordsche Streuformel
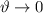 ist gleichbedeutend mit dem Grenzfall
ist gleichbedeutend mit dem Grenzfall 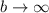 und ist daher nicht sinnvoll. Der Stossparameter sollte den halben
gegenseitigen Abstand der Streuatome nicht überschreiten. Für
und ist daher nicht sinnvoll. Der Stossparameter sollte den halben
gegenseitigen Abstand der Streuatome nicht überschreiten. Für 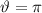 ,
d.h.
,
d.h. 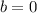 , erreicht
, erreicht 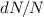 ein Minimum.
ein Minimum.
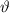 (Stossparametern
(Stossparametern 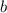 ) treten
Abweichungen auf.
) treten
Abweichungen auf.
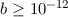 m sind Abschirmeffekte
des Coulomb-Potentials des Atomkerns durch Atomelektronen für die
Abweichungen zwischen Formel und Experiment verantwortlich.
m sind Abschirmeffekte
des Coulomb-Potentials des Atomkerns durch Atomelektronen für die
Abweichungen zwischen Formel und Experiment verantwortlich.
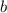 beruhen die Abweichungen zwischen
Formel und Experiment auf der Tatsache, dass die Modellannahme, dass
nur die abstossende Coulomb-Kraft für die Ablenkung der
beruhen die Abweichungen zwischen
Formel und Experiment auf der Tatsache, dass die Modellannahme, dass
nur die abstossende Coulomb-Kraft für die Ablenkung der 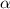 -Teilchen
verantwortlich ist, nicht mehr gültig ist. Es kommen neu sogenannte
anziehende Kernkräfte zum Tragen. Diese Abweichungen nennt man
anomale Rutherford-Streuung.
-Teilchen
verantwortlich ist, nicht mehr gültig ist. Es kommen neu sogenannte
anziehende Kernkräfte zum Tragen. Diese Abweichungen nennt man
anomale Rutherford-Streuung.
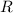 . Dieser
ist definiert als der Abstand, bei dem die Wirkung der Coulomb-Kraft und der
Kernkraft auf die
. Dieser
ist definiert als der Abstand, bei dem die Wirkung der Coulomb-Kraft und der
Kernkraft auf die 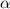 -Teilchen von der gleichen Grössenordnung sind. Man
erhält aus solchen Messungen für den Kernradius
-Teilchen von der gleichen Grössenordnung sind. Man
erhält aus solchen Messungen für den Kernradius 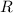 den folgenden Wert
den folgenden Wert
wobei 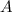 der Massenzahl entspricht.
der Massenzahl entspricht.
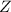 benutzt werden.
benutzt werden.
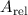 angegeben. Als
Einheit dient die atomare Masseneinheit 1 u = 1/12 der Masse eines
neutralen Kohlenstoffatoms. Der Zusammenhang zwischen der absoluten
und relativen Atommasse ist gegeben durch
angegeben. Als
Einheit dient die atomare Masseneinheit 1 u = 1/12 der Masse eines
neutralen Kohlenstoffatoms. Der Zusammenhang zwischen der absoluten
und relativen Atommasse ist gegeben durch 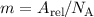 , wobei
, wobei 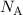 die Avogadro-Konstante bezeichnet.
die Avogadro-Konstante bezeichnet.
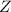 (auch
Ordnungszahl genannt) aufgeführt. Sie ist oberhalb jedes Atomsymbols
aufgeführt und entspricht der Anzahl Protonen (Elektronen). Die
Massenzahl
(auch
Ordnungszahl genannt) aufgeführt. Sie ist oberhalb jedes Atomsymbols
aufgeführt und entspricht der Anzahl Protonen (Elektronen). Die
Massenzahl 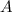 ist unterhalb jedes Atomsymbols aufgeführt. Sie ist die
der relativen Atommasse
ist unterhalb jedes Atomsymbols aufgeführt. Sie ist die
der relativen Atommasse 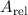 nächstgelegene ganze Zahl und entspricht
der Summe der Anzahl Protonen
nächstgelegene ganze Zahl und entspricht
der Summe der Anzahl Protonen 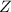 und Anzahl Neutronen
und Anzahl Neutronen 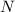 .
.
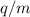 aufweisen. Sie stand
am Ursprung der Entdeckung der Isotopie (zwei Atome mit gleicher
Kernladungszahl
aufweisen. Sie stand
am Ursprung der Entdeckung der Isotopie (zwei Atome mit gleicher
Kernladungszahl 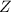 aber unterschiedlicher Massenzahl
aber unterschiedlicher Massenzahl 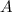 heissen
Isotope). Das Grundprinzip dieser Methode besteht darin, dass ein Strahl
geladener Teilchen mit unterschiedlichen Ladungs-Massenverhältnissen
heissen
Isotope). Das Grundprinzip dieser Methode besteht darin, dass ein Strahl
geladener Teilchen mit unterschiedlichen Ladungs-Massenverhältnissen
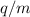 ein elektrisches und magnetisches Feld passiert und dadurch
räumlich getrennt wird. Neben der Analyse und Trennung von Isotopen
dient die Massenspektroskopie zur Analyse und Identifizierung von Stoffen
in der Chemie und der Restgas-Analyse in Vakuumsystemen in der Physik,
Chemie und Technik.
ein elektrisches und magnetisches Feld passiert und dadurch
räumlich getrennt wird. Neben der Analyse und Trennung von Isotopen
dient die Massenspektroskopie zur Analyse und Identifizierung von Stoffen
in der Chemie und der Restgas-Analyse in Vakuumsystemen in der Physik,
Chemie und Technik.
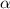 -Teilchen an Goldfolien und formulierte 1911
das nach ihm benannte Rutherfordsche Atommodell:
-Teilchen an Goldfolien und formulierte 1911
das nach ihm benannte Rutherfordsche Atommodell: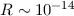 m, welcher beinahe
die gesamte Masse des Atoms enthält. Die Streuung von
m, welcher beinahe
die gesamte Masse des Atoms enthält. Die Streuung von 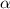 -Teilchen
erfolgt fast ausschliesslich an diesen Kernen.
-Teilchen
erfolgt fast ausschliesslich an diesen Kernen.
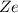 . Dabei bezeichnet
. Dabei bezeichnet
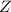 die Kernladungszahl.
die Kernladungszahl.
 -Teilchen und Atomkern ist rein
elektrostatisch und durch die Coulomb-Wechselwirkung bestimmt.
-Teilchen und Atomkern ist rein
elektrostatisch und durch die Coulomb-Wechselwirkung bestimmt.