In Kapitel 7 haben wir bereits die Struktur des Atoms kennengelernt. Ein Atom
besteht im Wesentlichen aus einem positiv geladenen Atomkern und den Atomkern
umkreisenden Elektronen. In diesem Kapitel knüpfen wir nun daran an. Wir werden
uns mit den Spektren der von Atomen ausgesandten elektromagnetischen Strahlung
auseinandersetzen. Die beobachteten diskreten Linienspektren deuten darauf hin,
dass Elektronen in einem Atom mit bestimmten diskreten Energiewerten an den
Atomkern gebunden sind. Dieses Phänomen konnte nicht mit den Mitteln der
klassischen Physik erklärt werden. Erst die Einführung der Quantenmechanik
erlaubte es ein tieferes Verständnis der elektronischen Eigenschaften von Atomen zu
gewinnen.
Als einfaches aber instruktives Beispiel zur Anwendung der Wellenmechanik von
Teilchen und einer ersten Nutzung der Quantenmechanik werden wir das Bohrsche
Atommodell zur Berechnung der grundlegenden Eigenschaften des Spektrums des
Wasserstoffatoms kennenlernen. Trotz seiner Einfachheit erlaubt dieses Modell nicht
nur die grundlegenden Eigenschaften von Wasserstoffatomen zu beschreiben, sondern
auch die von anderen Systemen, in denen eine positive Ladung von einer negativen
umkreist wird. Beispiele sind Rydberg-Atome oder Exzitonen in Halbleitern. Des
Weiteren diskutieren wir das Franck-Hertz-Experiment, in welchem die diskrete
Struktur der Bindungen von Elektronen im Atom in Stossexperimenten, im Einklang
mit dem Bohrschen Atommodell, beobachtbar ist. Wir betrachten ebenfalls eine
Erweiterung des Bohrschen Modells nach Arnold Sommerfeld und zeigen gleichzeitig
die Grenzen des Bohr-Sommerfeld-Modells auf. Anschliessend setzen wir uns mit
Rydberg-Atomen auseinander, die durch das Bohrsche Atommodell gut beschrieben
werden und auch ein Thema in der aktuellen Forschung sind. Zum Abschluss des
Kapitels folgt ein Exkurs zu den Einstein-Koeffizienten, die es erlauben die
Absorption und Emission von elektromagnetischer Strahlung in Atomen zu
beschreiben.
Im Allgemeinen beschreiben die in Messungen aufgenommenen Spektren von
atomaren oder molekularen Gasen die Frequenzabhängigkeit der Emission oder
Absorption von elektromagnetischer Strahlung in Atomen oder Molekülen. Diese
Spektren sind charakteristisch für die innere Struktur der Atome oder Moleküle.
Spektren können auch zur Untersuchung der Eigenschaften von Festkörpern und
Sternen aufgenommen werden. Optische Spektren sind eine wichtige Quelle für
Informationen über die elektronische Struktur und den Aufbau von Atomen und
daher ein wichtiges Hilfsmittel in der Atomphysik.
Zur Beobachtung von Emissionsspektren muss das zu untersuchende Objekt,
bzw. die zu untersuchende Substanz, zuvor angeregt worden sein. Dann
kann die Frequenzabhängigkeit der emittierten Strahlung untersucht werden.
Absorptionsspektren können aufgenommen werden, indem ein Objekt mit einem
kontinuierlichen Spektrum (z.B. dem eines schwarzen Strahlers) bestrahlt
wird und seine Absorption bei charakteristischen Frequenzen beobachtet
wird.
Häufig unterscheidet man drei verschiedene Typen von Spektren:
- Kontinuierliche Spektren
Heisse und dichte Objekte, z.B. leuchtende Festkörper oder Gase
mit hoher Dichte, zeigen ein kontinuierliches Spektrum. Solche
Spektren, wie z.B. das Spektrum der Sonne, lassen sich oft durch die
Schwarzkörperstrahlung annähern (siehe Kapitel 5).
- Linienspektren
Linienspektren sind typisch für Objekte bei niedrigen Temperaturen und
geringer Dichte, wie z.B. bei atomaren oder molekularen Gasen. Ein
solches Spektrum besteht aus einzelnen gut experimentell auflösbaren
diskreten Linien.
- Bandspektren
Bandenspektren können als eine teilweise kontinuierliche Überlagerung
von einer grossen Zahl von Linienspektren aufgefasst werden. Sie werden
vorwiegend in molekularen Gasen beobachtet.
In experimentell aufgenommenen Spektren wird die von einer Substanz emittierte
oder absorbierte Strahlungsleistung oder Intensität häufig gegen verschiedene für die
Frequenz der Strahlung charakteristische Messgrössen aufgetragen. Welche dieser
Grössen verwendet wird, hängt von den Gepflogenheiten der spezifischen
Fachrichtung ab.
- Wellenlänge
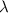
Die Wellenlänge wird in der Einheit m gemessen. Wellenlängenangaben
beziehen sich im allgemeinen auf das Vakuum
wobei der Brechungsindex 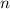 ebenfalls eine Funktion der Wellenlänge
ist (Dispersion). Gemessen werden solche Spektren mit Hilfe von
Beugungs-Gittern.
ebenfalls eine Funktion der Wellenlänge
ist (Dispersion). Gemessen werden solche Spektren mit Hilfe von
Beugungs-Gittern.
- Frequenz

Die Frequenz, welche im Gegensatz zur Wellenlänge nicht vom betrachteten
Medium abhängt, wird in der Einheit Hz gemessen. Der Zusammenhang zur
Wellenlänge ist gegeben durch
- Wellenzahl
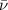
Die Wellenzahl wird in der Einheit 1/m gemessen und es gilt
- Energie
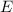
Die Energie 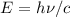 wird in der Einheit eV (Elektronenvolt) angegeben.
wird in der Einheit eV (Elektronenvolt) angegeben.
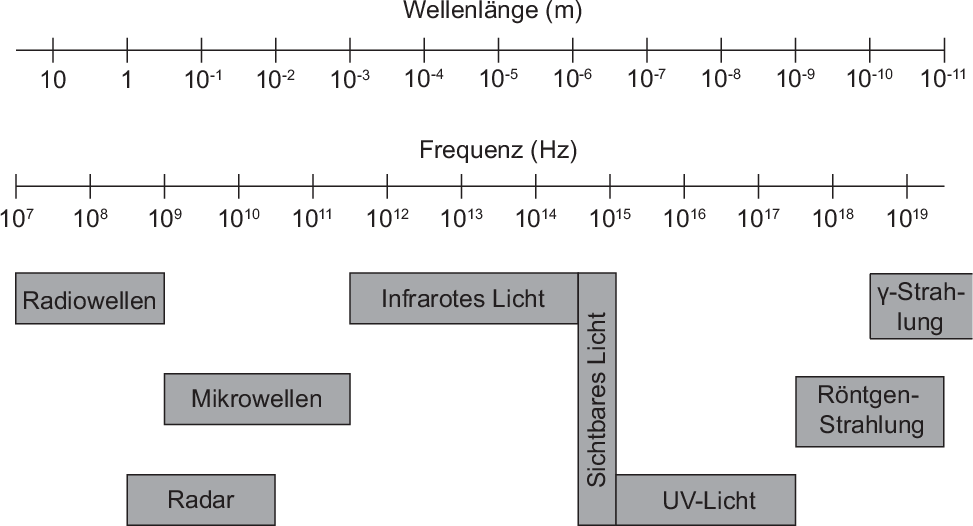
Spektren geben im gesamten Frequenzbereich elektromagnetischer Strahlung (siehe
Abb. 8.1), von Radiowellen bis Gammastrahlung, Auskunft über die Eigenschaften
von Substanzen.
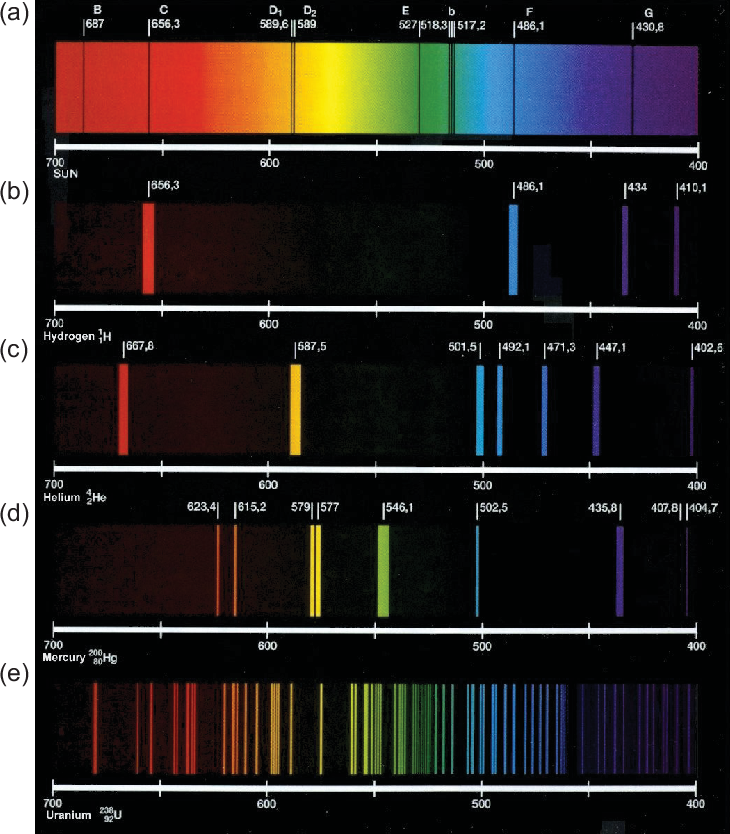
Nach den allgemeinen Bemerkungen zu den Spektren schauen wir uns als nächstes
ein paar Beispiele von Spektren an (siehe Abb. 8.2). Die Sonne als beinahe schwarzer
Strahler (siehe Abschnitt 5.4.7) zeigt ein kontinuierliches Spektrum. Atome, wie
z.B. Wasserstoff, Helium, Quecksilber oder Uran, zeigen wie für Atome typisch
Linienspektren, die sowohl in Absorption oder in Emission beobachtet werden
können.
Diskrete Emissions- und Absorptionsspektren von Atomen können nicht
mit Methoden der klassischen Physik erklärt werden. Klassische Theorien
würden beliebige Elektronenenergien und somit kontinuierliche Spektren
vorhersagen.
Man könnte aus der Tatsache, dass ein Atom bestimmte Frequenzen (Spektrallinien)
aussendet, schliessen, dass ein Atom als klassisches lineares Schwingsystem mit vielen
Freiheitsgraden aufgefasst werden kann. Doch selbst einfache Atome mit wenigen
Freiheitsgraden, wie z.B. das Wasserstoffatom, hat sehr viele Spektrallinien, die im
Oszillatormodell schwer zu verstehen wären. Selbst die Annahme, dass das Atom
durch ein anharmonisches Schwingsystem beschrieben sei, löst dieses Problem nicht.
Denn bei solchen Systemen hängen die Schwingungsperioden von den Amplituden ab,
so dass man keine scharfen Spektrallinien, sondern eher kontinuierliche Spektren
erwarten würde.
Nicht einmal die Stabilität des Elektrons auf seiner Bahn um den Atomkern, und
somit die Stabilität des Atoms selber, kann mit klassischen Methoden erklärt
werden.
Wir betrachten hier als Beispiel das einfachste Atom, das Wasserstoffatom. Es
besteht aus einem Proton, das von einem einzigen Elektron umkreist wird.
Wir nehmen an, dass sich das Elektron auf einer Kreisbahn mit zunächst
konstanter Winkelgeschwindigkeit bewegt. Für die zum Kern (Proton) gerichtete
Zentralbeschleunigung ist die Coulomb-Kraft verantwortlich. Der Kern ist einige
tausend Mal schwerer als das Elektron und kann daher als raumfest betrachtet
werden. Dieses System aus Proton und Elektron lässt sich somit als ein rotierender
elektrischer Dipol beschreiben. Die Kreisbewegung kann als Superposition einer
harmonischen Schwingung längs der x-Achse mit einer harmonischen Schwingung
längs der y-Achse aufgefasst werden (siehe Abb. 8.3). Ein oszillierender Dipol strahlt
elektromagnetische Wellen ab. Demzufolge verliert das Elektron auf seiner Bahn und
somit das Atom dauernd an Energie. Mit anderen Worten das Elektron verliert auf
seiner Bahn kinetische Energie und würde somit auf einer Spiralbahn mit
zunehmender Umlaufsfrequenz unaufhaltsam in den Kern stürzen. Wenn wir von
einem Bahnradius ausgehen, der etwa einem Atomradius entspricht, d.h. 1 Å , dann
wäre die Lebensdauer des Atoms von der Grössenordnung von 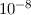 s. Dies
steht jedoch klar im Widerspruch mit der Tatsache, dass Atome (in ihrem
Grundzustand) stabil sind und dass Atome Licht bei diskreten Frequenzen
abstrahlen und kein kontinuierliches Spektrum haben (siehe Abschnitt 8.1.1).
s. Dies
steht jedoch klar im Widerspruch mit der Tatsache, dass Atome (in ihrem
Grundzustand) stabil sind und dass Atome Licht bei diskreten Frequenzen
abstrahlen und kein kontinuierliches Spektrum haben (siehe Abschnitt 8.1.1).
Hier bemerken wir, dass das von einem heissen Körper emittierte kontinuierliche
Spektrum auch von Atomen herrührt, die jedoch sehr stark miteinander gekoppelt
sind. Einzelne Atome haben jedoch diskrete Spektren.
Im Jahre 1908 fand Walter Ritz (Schweizer Mathematiker und Physiker) bei der
Betrachtung von Atomspektren eine Gesetzmässigkeit, die einen ersten Ansatzpunkt
zur Erklärung der Spektren von Atomen liefert. Diese wird auch als Ritzsches
Kombinationsprinzip bezeichnet:
Die Frequenz  jeder Spektrallinie eines Atoms lässt sich darstellen als die Differenz
zwischen zwei sogenannten Spektraltermen
jeder Spektrallinie eines Atoms lässt sich darstellen als die Differenz
zwischen zwei sogenannten Spektraltermen 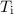 und
und 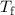
Jede Atomsorte hat einen für sie charakteristischen Satz von Spektraltermen
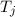 .
.
Als formales Beispiel betrachten wir ein System mit drei Spektraltermen 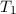 ,
, 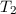 und
und 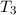 . Demzufolge lässt es folgende drei Frequenzen zu
. Demzufolge lässt es folgende drei Frequenzen zu
Aus 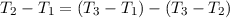 folgt, dass zwischen den drei Frequenzen die
folgende Beziehung gelten muss
folgt, dass zwischen den drei Frequenzen die
folgende Beziehung gelten muss
Aus diesen Betrachtungen ergibt sich folgende Interpretation für das
Kombinationsprinzip: Das System in unserem Beispiel hat drei diskrete Energieniveaus
 ,
,  und
und 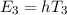 und kann unter Emission eines Photons von
einem Niveau in ein anderes übergehen, wobei die Energie
und kann unter Emission eines Photons von
einem Niveau in ein anderes übergehen, wobei die Energie 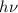 des Photons der
Differenz zwischen den beiden Energieniveaus entspricht (siehe Abb. 8.4).
des Photons der
Differenz zwischen den beiden Energieniveaus entspricht (siehe Abb. 8.4).
Bevor wir uns dem Bohrschen Atommodell zuwenden, welches die ersten
Erklärungsansätze zum Verständnis des Spektrums des Wasserstoffatoms lieferte,
setzen wir uns noch etwas genauer mit dem Wasserstoffatom auseinander.
Das Wasserstoffatom bestehend aus einem Proton und einem Elektron ist
das einfachste Atom. Es nahm daher während dem letzten Jahrhundert
immer wieder eine zentrale Rolle bei der Entwicklung von Atommodellen
ein.
Betrachten wir das Energieschema des Wasserstoffatoms (siehe Abb. 8.5) so
entspricht jedem Übergang zwischen einem Paar von Energieniveaus einer
Spektrallinie im Spektrum des Wasserstoffatoms. Im sichtbaren Wellenlängenbereich
gibt es drei charakteristische Linien (Wellenlängen: 656.3 nm, 486.1 nm und 434.0
nm), welche zusammen mit einer ganzen Schar von Linien im nahen UV-Bereich eine
sogenannte Serie von Spektrallinien bilden. Der Abstand der Linien dieser Serie
nimmt zu kleineren Wellenlängen ab, bis die Linien schlussendlich gegen einen
Grenzwert konvergieren. Diese Serie von Spektrallinien im Wasserstoffatom wird
Balmer-Serie genannt und wurde historisch, da sie im sichtbaren Frequenzbereich
liegt, als erste entdeckt. Der Namensgeber Johann Jakob Balmer (Schweizer
Mathematiker und Physiker) fand 1885 eine Formel für die Wellenlängen der
Serie
wobei 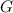 ein empirisch gefundener Zahlenwert ist.
ein empirisch gefundener Zahlenwert ist.
Weitere Untersuchungen zeigten, dass das Wasserstoffatom aus sehr vielen solchen
Serien besteht. Dabei spielte vor allem die Beobachtung von Licht, das von
astrophysikalischen Quellen ausgesandt wird, eine entscheidende Rolle, da es
zum Zeitpunkt dieser Untersuchungen schwierig war, auf der Erde reinen
Wasserstoff zu isolieren und experimentell zu untersuchen. Die Gesamtheit der
beobachteten Serien wird durch die sogenannte Rydberg-Formel, welche aus
rein empirischen Untersuchungen von Johannes Rydberg gefunden wurde,
beschrieben
wobei die ganzen Zahlen 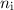 und
und 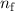 , die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und
, die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und 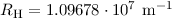 die
Rydberg-Konstante ist. Den Wert der Rydberg-Konstanten ermittelte Rydberg aus
experimentellen Daten des Wasserstoffspektrums. Die Rydberg-Kon-stante wird
auch häufig äquivalent in Einheiten von Energie, Wellenlänge oder Frequenz
angegeben.
die
Rydberg-Konstante ist. Den Wert der Rydberg-Konstanten ermittelte Rydberg aus
experimentellen Daten des Wasserstoffspektrums. Die Rydberg-Kon-stante wird
auch häufig äquivalent in Einheiten von Energie, Wellenlänge oder Frequenz
angegeben.
Die Balmer-Formel (8.9) ist ein Spezialfall der Rydberg-Formel (8.10) für 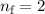 .
Die wichtigsten Serien beim Wasserstoffatom sind neben der Balmer-Serie die
Lyman-, Paschen-, Brackett und Pfund-Serie (siehe Tab. 8.1).
.
Die wichtigsten Serien beim Wasserstoffatom sind neben der Balmer-Serie die
Lyman-, Paschen-, Brackett und Pfund-Serie (siehe Tab. 8.1).
Der Vergleich der Rydberg-Formel (8.10) mit dem Ritzschen Kombinationsprinzip
aus Abschnitt 8.1.3 zeigt, dass der Ausdruck 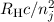 gerade den Spektraltermen
gerade den Spektraltermen
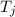 entspricht. Die Terme
entspricht. Die Terme 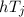 können somit als mögliche Energieniveaus des
Elektrons im Atom interpretiert werden für die das Bohrsche Atommodell eine erste
Erklärung lieferte.
können somit als mögliche Energieniveaus des
Elektrons im Atom interpretiert werden für die das Bohrsche Atommodell eine erste
Erklärung lieferte.
Das Bohrsche Atommodell war das erste einfache Modell zur Erklärung des
Spektrums des Wasserstoffatoms. Es wurde vom dänischen Physiker Niels Bohr um
1913 entwickelt. Einerseits ging er vom (klassischen) Rutherfordschen Atommodell
(siehe Abschnitt 7.5.2) aus, indem er annahm, dass sich im Wasserstoffatom das
negativ geladene Elektron auf einer Kreisbahn um den positiv geladenen Kern
bewegt. Andererseits formulierte er ausgehend von den experimentellen Erkenntnissen
über atomare Spektren drei Postulate. Das Modell wird daher auch oft als
semiklassisches Atommodell bezeichnet.
Wir beginnen mit dem klassischen Modell für die Bahnbewegung des Elektrons im
Wasserstoffatom. Das Elektron bewegt sich auf einer Kreisbahn um das Proton (siehe
Abb. 8.3). Diese Kreisbahn ergibt sich aus dem Gleichgewicht zwischen
der anziehenden Coulomb-Kraft 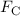 zwischen Elektron und Kern, und der
Zentripetalkraft
zwischen Elektron und Kern, und der
Zentripetalkraft 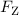 , die das Elektrons mit Masse
, die das Elektrons mit Masse 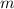 und Geschwindigkeit
und Geschwindigkeit  auf
seiner Bahn mit Radius
auf
seiner Bahn mit Radius  wahrnimmt
wahrnimmt
Daraus ergibt sich die folgende Bedingung für die Geschwindigkeit  des Elektrons,
um bei einem gegebenem Bahnradius
des Elektrons,
um bei einem gegebenem Bahnradius  zu einer stabilen Kreisbahn zu
führen
zu einer stabilen Kreisbahn zu
führen
Die Gesamtenergie des Elektrons auf einer solchen Bahn setzt sich aus kinetischer
und potentieller Energie zusammen. Für die kinetische Energie erhalten wir
mit (8.12)
Die potentielle Enegie 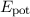 entspricht der Arbeit, die man gewinnt, wenn man das
Elektron aus dem Unendlichen unter Einwirkung der Coulomb-Kraft
entspricht der Arbeit, die man gewinnt, wenn man das
Elektron aus dem Unendlichen unter Einwirkung der Coulomb-Kraft 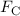 zum
Abstand
zum
Abstand  vom Kern bringt
vom Kern bringt
Dies entspricht der Bindungsenergie
und nimmt dementsprechend einen negativen Wert an. Damit erhalten wir für die
Gesamtenergie in diesem klassischen Modell
Wie wir in Abschnitt 8.1.2 gesehen haben, ist es mit einem solchen Modell
zusammen mit den Gesetzen aus der klassischen Elektrodynamik nicht möglich die
Stabilität von Atomen und insbesondere die Charakteristiken von atomaren
Spektren zu erklären. Um diese Lücke zwischen der klassischen Physik und
den experimentellen Beobachtungen zu schliessen, formulierte Bohr drei
Postulate:
- Elektronen in Atomen erfüllen zwar die klassischen Bewegungsgleichungen,
es sind aber nur ganz bestimmte diskrete Bahnen mit den Energien
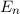 , die Energieterme des Atoms, erlaubt. Wie bei Rydberg wird
, die Energieterme des Atoms, erlaubt. Wie bei Rydberg wird 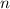 Hauptquantenzahl genannt.
Hauptquantenzahl genannt.
- Die Bewegung der Elektronen auf diesen Bahnen erfolgt strahlungslos. Es ist
jedoch für das Elektron möglich unter Emission von Strahlung (d.h. unter
Aussendung von Photonen) von einer Bahn mit geringerer Bindungsenergie
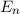 (also grösserem
(also grösserem  ) auf eine Bahn mit grösserer Bindungsenergie
) auf eine Bahn mit grösserer Bindungsenergie 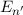 (kleinerem
(kleinerem  ) zu gelangen. Für das bei diesem Übergang emittierte Photon gilt
der folgende Zusammenhang
) zu gelangen. Für das bei diesem Übergang emittierte Photon gilt
der folgende Zusammenhang
Bei der Absorption von Photonen erfolgt der umgekehrte Prozess. Aus
dem Vergleich mit der Rydberg-Formel (8.10) schrieb Bohr für die
Energieterme
wobei 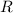 die Rydberg-Konstante bezeichnet. Das Minuszeichen zeigt an, dass
es sich dabei um Bindungsenergien handelt.
die Rydberg-Konstante bezeichnet. Das Minuszeichen zeigt an, dass
es sich dabei um Bindungsenergien handelt.
- Aus klassischer Sicht müsste die Umlauffrequenz der Elektronen auf
den klassischen Kreisbahnen gleich der Frequenz der emittierten oder
absorbierten Strahlung sein, was beim Wasserstoffatom insbesondere bei
kleinen Bahnradien nicht zutrifft. Nach Bohr gilt aber: Mit wachsendem
Bahnradius (d.h. mit wachsender Hauptquantenzahl n) stimmen diese beiden
Frequenzen überein oder allgemein ausgedrückt mit wachsendem Bahnradius
(d.h. mit wachsender Hauptquantenzahl
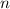 ) gehen die Gesetze der
Quantenmechanik in diejenige der klassischen Mechanik über. Dieses Prinzip
wird Korrespondenzprinzip genannt. Insbesondere lässt sich durch
das Korrespondenzprinzip mit Hilfe der ersten beiden Postulate die
Rydberg-Konstante
) gehen die Gesetze der
Quantenmechanik in diejenige der klassischen Mechanik über. Dieses Prinzip
wird Korrespondenzprinzip genannt. Insbesondere lässt sich durch
das Korrespondenzprinzip mit Hilfe der ersten beiden Postulate die
Rydberg-Konstante 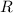 in (8.17) und (8.18) und damit auch die
Energieniveaus
in (8.17) und (8.18) und damit auch die
Energieniveaus 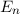 des Wasserstoffatoms durch atomaren Grössen
ausdrücken.
des Wasserstoffatoms durch atomaren Grössen
ausdrücken.
Ausgehend von diesen Postulaten berechnen wir nun die Rydberg-Konstante und
drücken sie durch atomare Grössen aus. Wir betrachten den Übergang eines
Elektrons zwischen benachbarten Bahnen, d.h. 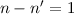 , bei grossem
, bei grossem 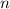 .
Aus (8.16), (8.17) und (8.18) erhalten wir für die Frequenz der dabei emittierten
Strahlung
.
Aus (8.16), (8.17) und (8.18) erhalten wir für die Frequenz der dabei emittierten
Strahlung
Als nächstes drücken wir den (klassischen) Ausdruck für die Energie 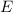 in (8.15) in
Abhängigkeit der (klassischen) Frequenz
in (8.15) in
Abhängigkeit der (klassischen) Frequenz 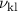 aus. Mit
aus. Mit 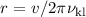 und (8.12)
erhalten wir
und (8.12)
erhalten wir
Auflösen nach dem Bahnradius  ergibt
ergibt
Einsetzen in (8.15) liefert schliesslich für die Energie 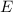 den Ausdruck
den Ausdruck
Nach Postulat 3 nehmen wir nun an, dass mit wachsender Hauptquantenzahl 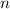 die Gesetze der Quantenmechanik in diejenige der klassischen Mechanik
übergehen und können deshalb
die Gesetze der Quantenmechanik in diejenige der klassischen Mechanik
übergehen und können deshalb 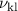 in (8.22) durch den Ausdruck in (8.19)
ersetzen
in (8.22) durch den Ausdruck in (8.19)
ersetzen
Gleichsetzen mit (8.17) ergibt
Daraus erhalten wir für die Rydberg-Konstante 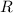 den folgenden Ausdruck
den folgenden Ausdruck
Dieser Ausdruck ist in guter Übereinstimmung mit dem empirisch gemessenen Wert
aus Abschnitt 8.2.
Ebenfalls erhalten wir einen Ausdruck für den n-ten Bahnradius 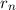 des Elektrons
im Wasserstoffatom. Gleichsetzen von (8.15) und (8.17) ergibt
des Elektrons
im Wasserstoffatom. Gleichsetzen von (8.15) und (8.17) ergibt
Einsetzen von (8.25) liefert für den n-ten Bahnradius 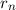
wobei der kleinste Bahnradius 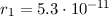 m Bohrscher Radius genannt wird
und üblicherweise mit
m Bohrscher Radius genannt wird
und üblicherweise mit 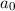 bezeichnet wird.
bezeichnet wird.
Weiter ergibt sich mit (8.12) und (8.27) für den Betrag des Bahndrehimpulses 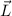 des Elektrons
des Elektrons
Mit 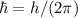 ergibt sich
ergibt sich
D.h. der Bahndrehimpuls ist ein ganzzahliges Vielfaches von 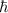 .
.
Als nächstes schauen wir uns zur besseren Veranschaulichung noch eine zweite
gleichwertige Formulierung des Bohrschen Atommodells an. Wir betrachten die
Bahnbewegung des Elektrons wiederum klassisch. Die Coulomb-Kraft ist
verantwortlich für eine Kreisbewegung und die Bahngeschwindigkeit ist gegeben
durch (8.12)
Ebenfalls ist die Gesamtenergie des Elektrons gegeben durch (8.15)
Als nächstes kommen wir zu den 3 Postulaten von Bohr. An den ersten beiden
Postulaten wird im Wesentlichen festgehalten: Für das Elektron im Wasserstoffatom
sind nur ganz bestimmte diskrete Bahnen mit den Energie 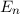 erlaubt, die
Bewegung auf diesen Bahnen erfolgt strahlungslos, jedoch kann Strahlung beim
Übergang eines Elektrons von einer Bahn auf eine andere emittiert oder absorbiert
werden, für diesen Übergang gilt
erlaubt, die
Bewegung auf diesen Bahnen erfolgt strahlungslos, jedoch kann Strahlung beim
Übergang eines Elektrons von einer Bahn auf eine andere emittiert oder absorbiert
werden, für diesen Übergang gilt 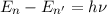 und die Energieniveaus sind nach
Rydberg gegeben durch
und die Energieniveaus sind nach
Rydberg gegeben durch 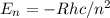 .
.
In der vorherigen Betrachtung resultierten nun die charakteristischen Grössen für die
Elektronenbahnen (Rydberg-Konstante (Energie), Radius, Bahndrehimpuls) aus der
Annahme, dass mit wachsendem Bahnradius (wachsender Hauptquantenzahl 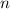 ) die
Gesetze der Quantenmechanik in diejenige der klassischen Mechanik übergehen und
der daraus resultierenden Grenzbetrachtung: Gleichsetzen der Umlauffrequenz auf
den klassischen Kreisbahnen mit der (quantenmechanischen) Frequenz der
emittierten oder absorbierten Strahlung für hohe
) die
Gesetze der Quantenmechanik in diejenige der klassischen Mechanik übergehen und
der daraus resultierenden Grenzbetrachtung: Gleichsetzen der Umlauffrequenz auf
den klassischen Kreisbahnen mit der (quantenmechanischen) Frequenz der
emittierten oder absorbierten Strahlung für hohe 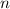 .
.
Anstelle dieser Grenzbetrachtung tritt zur Bestimmung der Elektronenbahnen nun
folgende gleichwertige Betrachtung: Wir betrachten die de Broglie-Wellenlänge 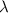 des Elektrons auf seiner klassischen Bahn um den Atomkern
des Elektrons auf seiner klassischen Bahn um den Atomkern
Mit (8.30) erhalten wir
Für das Elektron im Wasserstoffatom sind nun nur die Bahnradien  erlaubt für
die die Materiewelle des Elektrons mit sich selbst konstruktiv interferiert, d.h. die
Länge der Umlaufbahn
erlaubt für
die die Materiewelle des Elektrons mit sich selbst konstruktiv interferiert, d.h. die
Länge der Umlaufbahn 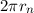 muss einem ganzzahligen Vielfachen der de
Broglie-Wellenlänge
muss einem ganzzahligen Vielfachen der de
Broglie-Wellenlänge 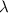 des Elektrons entsprechen. Oder in anderen Worten
ausgedrückt: Die Materiewelle muss nach einer Umdrehung wieder auf sich selber
treffen. Demzufolge lautet die Gleichung zur Bestimmung der Bahnradien
des Elektrons entsprechen. Oder in anderen Worten
ausgedrückt: Die Materiewelle muss nach einer Umdrehung wieder auf sich selber
treffen. Demzufolge lautet die Gleichung zur Bestimmung der Bahnradien 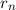 (Interferenzbedingung)
(Interferenzbedingung)
Wenn die Länge der Umlaufbahn kein ganzzahliges Vielfaches der de
Broglie-Wellenlänge ist, tritt destruktive Interferenz auf und die Bahn existiert nicht.
Aus (8.34) erhalten wir mit (8.33) in Übereinstimmung mit (8.27) für den n-ten
Bahnradius  des Elektrons
des Elektrons
Der Bahnradius 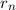 ist also quadratisch in der Hauptquantenzahl
ist also quadratisch in der Hauptquantenzahl 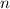 des Elektrons
im Wasserstoffatom.
des Elektrons
im Wasserstoffatom.
Analog zu (8.28) und (8.29) ergibt sich auch die Quantisierung des Betrags des
Bahndrehimpulses 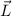 zu:
zu: 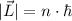 .
.
Für die Gesamtenergie 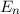 des Elektrons im Wasserstoffatom ergibt sich mit (8.35)
aus (8.31)
des Elektrons im Wasserstoffatom ergibt sich mit (8.35)
aus (8.31)
Gleichsetzen mit der Rydberg-Formulierung (8.17) ergibt in Übereinstimmung
mit (8.25) für die Rydberg-Konstante
Dabei ist zu beachten, dass die Energie des Elektrons 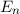 umgekehrt proportional
ist zum Quadrat der Hauptquantenzahl
umgekehrt proportional
ist zum Quadrat der Hauptquantenzahl 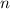 . Dieses Verhalten ist charakteristisch für
die
. Dieses Verhalten ist charakteristisch für
die  -Abhängigkeit des Coulomb-Potentials.
-Abhängigkeit des Coulomb-Potentials.
- Strahlung wird von einem Atom emittiert oder absorbiert, wenn
Elektronen ihre Bahn bzw. ihr Energieniveau wechseln.
- Bei Absorptionsübergängen gibt ein Photon seine Energie
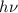 an ein
Elektron weiter, welches dadurch von einem tiefer liegenden Energieniveau
in ein höher liegendes Energieniveau wechselt.
an ein
Elektron weiter, welches dadurch von einem tiefer liegenden Energieniveau
in ein höher liegendes Energieniveau wechselt.
- Bei Emissionsübergängen fällt ein Elektron von einem höher liegenden
Energieniveau unter Abgabe eines Photons der Energie
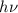 in ein tiefer
liegendes Energieniveau. Das Elektron muss zuvor durch Energiezufuhr
auf dieses höhere Energieniveau gebracht worden sein.
in ein tiefer
liegendes Energieniveau. Das Elektron muss zuvor durch Energiezufuhr
auf dieses höhere Energieniveau gebracht worden sein.
- Die eingezeichneten
Elektronenübergänge im Energieschema des Wasserstoffatoms in Abb. 8.5
sind demzufolge ausschliesslich Emissionsübergänge.
- Bei Raumtemperatur (
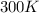 ) ist nur der Grundzustand
des Wasserstoffatoms (
) ist nur der Grundzustand
des Wasserstoffatoms (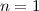 ) besetzt. Deshalb kann man bei normalen
Temperaturen nur die Lyman-Serie in Absorption beobachten. Bei höheren
Temperaturen, wie sie z.B. in der Atmosphäre von Sternen vorkommen,
ist auch der erste angeregte Zustand des Wasserstoffs (
) besetzt. Deshalb kann man bei normalen
Temperaturen nur die Lyman-Serie in Absorption beobachten. Bei höheren
Temperaturen, wie sie z.B. in der Atmosphäre von Sternen vorkommen,
ist auch der erste angeregte Zustand des Wasserstoffs (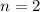 ) besetzt
und weitere Spektrallinien können beobachtet werden.
) besetzt
und weitere Spektrallinien können beobachtet werden.
Wie bereits erwähnt lässt sich das Bohrsche Atommodell auch zur Erklärung der
Spektren anderer wasserstoffähnlicher Systeme verwenden. Ein Beispiel sind Ionen
mit einem einzigen verbleibenden Elektron, das sich mit einer Geschwindigkeit 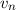 auf einer Kreisbahn mit Radius
auf einer Kreisbahn mit Radius 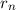 um einen positiv geladenen Kern mit
Kernladungszahl
um einen positiv geladenen Kern mit
Kernladungszahl 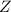 bewegt (z.B. He
bewegt (z.B. He oder Li
oder Li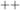 (siehe Abb. 8.6)).
(siehe Abb. 8.6)).
Aus dem Kräftegleichgewicht ergibt sich unter Beachtung der Kernladung
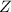
für die Bahngeschwindigkeit 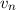 einer stabilen Bahn des Elektrons
einer stabilen Bahn des Elektrons
Die analoge Rechnung wie in Abschnitt 8.3 führt zu folgendem Ausdruck für die
Bahnradien 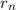 des Elektrons
des Elektrons
Die Gesamtenergie 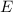 ist nach (8.13), (8.14) und (8.15) gegeben durch
ist nach (8.13), (8.14) und (8.15) gegeben durch
Einsetzen von (8.39) und (8.40) ergibt
Zum Abschluss geben wir noch die Frequenz  der emittierten oder absorbierten
Strahlung bei einem Elektronenübergang an. Mit (8.42) ergibt sich aus (8.16)
der emittierten oder absorbierten
Strahlung bei einem Elektronenübergang an. Mit (8.42) ergibt sich aus (8.16)
wobei 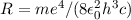 die Rydberg-Konstante ist. Somit erkennen wir, dass die
Bindungsenergie und auch die Energie der emittierten Photonen wie
die Rydberg-Konstante ist. Somit erkennen wir, dass die
Bindungsenergie und auch die Energie der emittierten Photonen wie 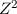 mit der
Kernladungszahl des ionisierten Atoms skaliert. Daher haben Ionen immer deutlich
höhere Übergangsfrequenzen als neutrale Atome.
mit der
Kernladungszahl des ionisierten Atoms skaliert. Daher haben Ionen immer deutlich
höhere Übergangsfrequenzen als neutrale Atome.
Bisher haben wir idealisiert angenommen, dass der Kern, um den sich das Elektron
bewegt in Ruhe ist. Dies ist nur der Fall, wenn der Kern unendlich schwer wäre. In
der Realität hat der Kern aber eine endliche Masse und bewegt sich mit dem
Elektron um einen gemeinsamen Schwerpunkt. Wir berücksichtigen diese
Mitbewegung des Kerns im Bohrschen Atommodell. Die dadurch hervorgerufene
Korrektur der Rydberg-Konstante kann den Unterschied zwischen dem gemessenen
Wert für die Rydberg-Konstante 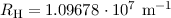 (siehe Abschnitt 8.2) und
dem theoretischen Wert
(siehe Abschnitt 8.2) und
dem theoretischen Wert 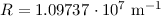 aus (8.25) beim Wasserstoffatom
erklären. Ausserdem erlaubt diese Betrachtung aus der genauen Vermessung des
elektronischen Spektrums eines Atoms, Isotope mit unterschiedlichen Kernmassen
experimentell nachzuweisen.
aus (8.25) beim Wasserstoffatom
erklären. Ausserdem erlaubt diese Betrachtung aus der genauen Vermessung des
elektronischen Spektrums eines Atoms, Isotope mit unterschiedlichen Kernmassen
experimentell nachzuweisen.
Die Bewegung des Kerns und des Elektrons mit den Massen 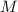 und
und 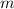 und Abstand
und Abstand  kann aufgefasst werden als die Bewegung eines fiktiven
Teilchens, das den Schwerpunkt im Abstand
kann aufgefasst werden als die Bewegung eines fiktiven
Teilchens, das den Schwerpunkt im Abstand  umläuft und die reduzierte
Masse
umläuft und die reduzierte
Masse 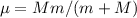 besitzt. Die Masse
besitzt. Die Masse 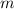 des Elektrons muss also
durch die reduzierte Masse
des Elektrons muss also
durch die reduzierte Masse 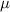 ersetzt werden. Damit erhalten wir für die
korrigierte Rydberg-Konstante, die wir mit
ersetzt werden. Damit erhalten wir für die
korrigierte Rydberg-Konstante, die wir mit 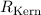 bezeichnen, folgenden
Ausdruck
bezeichnen, folgenden
Ausdruck
Für das Wasserstoffatom ist für 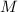 die Protonenmasse einzusetzen. Es ergibt sich
der folgende Wert
die Protonenmasse einzusetzen. Es ergibt sich
der folgende Wert
was in dieser Genauigkeit mit dem gemessenen Wert 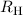 übereinstimmt.
übereinstimmt.
Nach dieser Betrachtung können wir folgendes Fazit ziehen: Die Spektren aller
Einelektronensysteme (Atome oder Ionen mit einem einzigen Elektron) stimmen bis
auf den Faktor 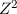 und die Rydberg-Konstante
und die Rydberg-Konstante 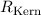 überein
überein
Dies deckt sich mit den experimentellen Resultaten. Insbesondere wurden für He diverse Serien von Spektrallinien gefunden die durch (8.46) beschrieben werden. Wie
bereits erwähnt, können solche Bohrschen Atommodelle auch andere Phänomene
erklären, z.B. wenn in einem Halbleiter ein einzelnes Elektron mit einem positiv
geladenen Kern einen gebundenen Zustand bildet und damit ein sogenanntes Exziton
formt.
diverse Serien von Spektrallinien gefunden die durch (8.46) beschrieben werden. Wie
bereits erwähnt, können solche Bohrschen Atommodelle auch andere Phänomene
erklären, z.B. wenn in einem Halbleiter ein einzelnes Elektron mit einem positiv
geladenen Kern einen gebundenen Zustand bildet und damit ein sogenanntes Exziton
formt.
Betrachtet man die optischen Spektren von Atomen mit einer höheren Auflö-sung, so
zeigt sich, dass einzelne Linien eine Substruktur aus mehreren Linien aufweisen, die
sogenannte Feinstruktur. Aufgrund der Beobachtung solcher Feinstrukturen beim
Wasserstoffatom und beim He -Ion postulierte Sommerfeld um 1915 eine
Erweiterung des Bohrschen Atommodells.
-Ion postulierte Sommerfeld um 1915 eine
Erweiterung des Bohrschen Atommodells.
Im Bohrschen Atommodell haben wir angenommen, dass sich die Elektronen auf
Kreisbahnen um den Kern bewegen. Aus der Betrachtung der mechanischen Gesetze
folgerte Sommerfeld, dass neben den Kreisbahnen auch Ellipsenbahnen möglich sind.
Zur Beschreibung dieser Bahnen ist neben der Hauptquantenzahl 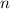 eine
zweite Quantenzahl notwendig. Die Hauptquantenzahl bestimmt weiterhin die
Gesamtenergie
eine
zweite Quantenzahl notwendig. Die Hauptquantenzahl bestimmt weiterhin die
Gesamtenergie 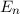 nach der Formel
nach der Formel
Zugleich bestimmt sie auch die grosse Hauptachse 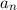 der Ellipse. Zur Festlegung
der kleinen Hauptachse
der Ellipse. Zur Festlegung
der kleinen Hauptachse 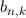 ist nun die neue Quantenzahl
ist nun die neue Quantenzahl 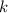 verantwortlich: Der
Betrag des Bahndrehimpulses muss ein Vielfaches von
verantwortlich: Der
Betrag des Bahndrehimpulses muss ein Vielfaches von 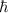 sein
sein
Der Vergleich mit (8.29) zeigt, dass wenn 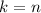 ist, die Ellipsenbahn zu einem
Kreis wird. Zusammenfassend können wir sagen, dass zu jeder Hauptquantenzahl
ist, die Ellipsenbahn zu einem
Kreis wird. Zusammenfassend können wir sagen, dass zu jeder Hauptquantenzahl 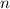 (und damit zur Energie
(und damit zur Energie 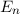 ) eine grosse Hauptachse
) eine grosse Hauptachse 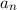 gehört, jedoch
verschiedene kleine Hauptachsen
gehört, jedoch
verschiedene kleine Hauptachsen 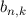 , welche durch die zweite Quantenzahl
, welche durch die zweite Quantenzahl 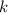 festgelegt werden.
festgelegt werden.
Wir wissen nun, dass zu jeder Energie 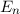 zwar verschiedene Bahnen gehören,
jedoch ist die Zahl der beobachtbaren Linien im Spektrum gleich geblieben, d.h. das
bisherige Modell liefert noch keine Erklärung für die anfangs erwähnte Feinstruktur
in atomaren Spektren. Sommerfeld postulierte 1916 daher eine weitere Erweiterung:
Die Berücksichtigung der bisher vernachlässigten Relativitätstheorie. Dadurch wird
die Masse
zwar verschiedene Bahnen gehören,
jedoch ist die Zahl der beobachtbaren Linien im Spektrum gleich geblieben, d.h. das
bisherige Modell liefert noch keine Erklärung für die anfangs erwähnte Feinstruktur
in atomaren Spektren. Sommerfeld postulierte 1916 daher eine weitere Erweiterung:
Die Berücksichtigung der bisher vernachlässigten Relativitätstheorie. Dadurch wird
die Masse 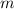 zu einer Grösse die von der Geschwindigkeit abhängt. Ein qualitatives
Verständnis liefert die Anwendung des 2. Keplerschen Gesetzes auf Atome: Zieht man
eine Verbindungslinie zwischen Kern und Elektron so überstreicht diese in gleichen
Zeiten gleich grosse Flächen. Folglich bewegen sich die Elektronen auf ihren
Ellipsenbahnen näher am Kern schneller und sind daher auch schwerer. Dies
führt zu einer Änderung der Bahnform und der Energie: Das Elektron führt
eine Art Rosettenbewegung durch und für die Energie
zu einer Grösse die von der Geschwindigkeit abhängt. Ein qualitatives
Verständnis liefert die Anwendung des 2. Keplerschen Gesetzes auf Atome: Zieht man
eine Verbindungslinie zwischen Kern und Elektron so überstreicht diese in gleichen
Zeiten gleich grosse Flächen. Folglich bewegen sich die Elektronen auf ihren
Ellipsenbahnen näher am Kern schneller und sind daher auch schwerer. Dies
führt zu einer Änderung der Bahnform und der Energie: Das Elektron führt
eine Art Rosettenbewegung durch und für die Energie 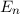 ergibt sich nach
Sommerfeld
ergibt sich nach
Sommerfeld
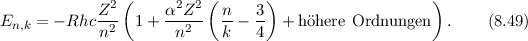
Dabei bezeichnet  die Feinstrukturkonstante, welche gegeben ist durch
die Feinstrukturkonstante, welche gegeben ist durch
Die Grössenordnung dieser relativistischen Korrekutur ist 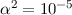 und daher eher
klein.
und daher eher
klein.
Mit dem Bohrschen Atommodell inkl. den Erweiterungen durch Sommerfeld ist es
möglich das Spektrum des Wasserstoffatoms zu beschreiben. Bei der Betrachtung von
anderen Atomen kommen jedoch schnell die Grenzen dieses Modells zum Vorschein,
auf die wir nun im nächsten Abschnitt eingehen.
Das Bohr-Sommerfeld-Modell beschreibt einige grundlegende Eigenschaften des
Wasserstoffatoms in guter Näherung. Das Modell erlaubt es aber nicht korrekte
Vorhersagen für Atome mit mehreren Elektronen zu treffen.
Selbst beim Wasserstoffatom macht das Modell nur Aussagen über die Frequenz der
emittierten oder absorbierten Strahlung. Angaben über relative Intensitäten der von
verschiedenen Übergängen emittierten Strahlung können kaum gemacht werden. Bohr
versuchte diese Schwachpunkte durch das Korrespondenzprinzip auszumerzen. Wie in
Abschnitt 8.3 werden dazu Grössen wie Frequenz oder auch Strahlungsintensität
klassisch berechnet und durch Grenzbetrachtungen in die Quantentheorie
übertragen.
Ebenfalls ist die Beschreibung der Eigenschaften des Wasserstoffs in elektrischen oder
magnetischen Feldern in diesem Modell nur begrenzt möglich. Abhilfe schafft nur eine
Betrachtung eines Modells, das ausschliesslich auf der Quantenmechanik basiert(siehe
Kapitel 9).
In diesem Abschnitt betrachten wir Atome bei denen sich ein Elektron in einem
Zustand mit einer sehr grossen Hauptquantenzahl 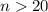 befindet. Solche
Atome werden Rydberg-Atome genannt und sind ein wichtiger Bestandteil der
Grundlagenforschung über die Wechselwirkung einzelner Photonen mit einzelnen
Atomen. Rydberg-Atome besitzen folgende Eigenschaften:
befindet. Solche
Atome werden Rydberg-Atome genannt und sind ein wichtiger Bestandteil der
Grundlagenforschung über die Wechselwirkung einzelner Photonen mit einzelnen
Atomen. Rydberg-Atome besitzen folgende Eigenschaften:
- Das Elektron mit der grossen Hauptquantenzahl bewegt sich auf einer
Bahn mit sehr grossem Radius
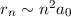 . In Experimenten wurden
bereits Rydberg-Atome mit einem Durchmesser von bis zu
. In Experimenten wurden
bereits Rydberg-Atome mit einem Durchmesser von bis zu 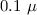 m
erzeugt. Dadurch sind Rydberg-Atome im Vergleich zu einem Atom im
Grundzustand bis
m
erzeugt. Dadurch sind Rydberg-Atome im Vergleich zu einem Atom im
Grundzustand bis 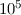 mal grösser.
mal grösser.
- Dieses Elektron auf Bahnen mit grossen Radien befindet sich weit
ausserhalb des Atomrumpfs und der anderen Elektronen. Es bewegt sich
also im Feld des Kerns, welcher durch alle anderen Elektronen abgeschirmt
wird und deshalb effektiv die Ladung
 besitzt. Rydberg-Atome
verhalten sich also wie Wasserstoffatome mit hoher Hauptquantenzahl
besitzt. Rydberg-Atome
verhalten sich also wie Wasserstoffatome mit hoher Hauptquantenzahl
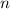 und können durch das Bohr-Sommerfeld-Modell annähernd gut
beschrieben werden.
und können durch das Bohr-Sommerfeld-Modell annähernd gut
beschrieben werden.
- Rydberg-Atome zeichnen sich durch hohe Dipolmomente
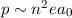 aus
und zeigen daher eine sehr starke Wechselwirkung mit Licht.
aus
und zeigen daher eine sehr starke Wechselwirkung mit Licht.
- Ändert das äusserste Elektron seine Bahn und emittiert Licht, so liegen die
Übergangsfrequenzen im fernen Infrarot- oder Mikrowellenbereich. Zum Beispiel
ergibt sich für ein Elektron mit Hauptquantenzahl
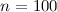 beim wechseln der
Bahn (Verringerung der Hauptquantenzahl
beim wechseln der
Bahn (Verringerung der Hauptquantenzahl 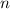 um 1) nach (8.19) eine
Übergangsfrequenz
um 1) nach (8.19) eine
Übergangsfrequenz  von
von
- Rydberg-Atome weisen lange Lebensdauern von bis zu einer Sekunde auf. Diese
langen Lebensdauern sind auch durch die niedrigen Übergangsfrequenzen der
Rydberg-Atome begründet und der daraus resultierenden geringeren spontanen
Emissionsrate. Im Vergleich dazu leben niedrigere Anregungszustände von
Atomen etwa
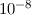 s.
s.
- Rydberg-Atome können leicht ionisiert werden, da die Bindungsenergie
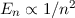 bei grossen
bei grossen 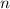 sehr klein wird.
sehr klein wird.
In der Realität kann man Rydberg-Atome mit Hauptquantenzahlen 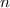 bis zu 350
beobachten. Mit Hilfe von Rydberg-Atome konnte man Grössen wie Energieniveaus
oder Lebensdauern für Quantenzahlen experimentell bestimmen, die bis dahin nur
theoretisch zugänglich waren.
bis zu 350
beobachten. Mit Hilfe von Rydberg-Atome konnte man Grössen wie Energieniveaus
oder Lebensdauern für Quantenzahlen experimentell bestimmen, die bis dahin nur
theoretisch zugänglich waren.
Bisher haben wir in spektroskopischen Experimenten beobachtet, dass die
Bindungsenergie von Elektronen in Atomen quantisiert ist. Wir betrachten nun ein
Elektronenstoss-Versuch, mit welchem James Franck und Gustav Hertz 1914 (unabhängig
von optischer Spektroskopie) die Existenz von diskreten Energieniveaus im Atom
nachwiesen.
Beim Franck-Hertz-Experiment (siehe Abb. 8.7) werden in einer mit Quecksilberdampf
(von kleinem Druck) gefüllten Röhre Elektronen von der Glühkathode K emittiert
und im elektrischen Feld zwischen Kathode K und Gitter G beschleunigt. Weiter
aussen befindet sich die Auffängerelektrode A, die gegen das Gitter eine negative
Spannung von 0.5 V hat.
Gemessen wird nun der Strom 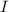 im Auffängerkreis als Funktion der
Beschleunigungsspannung
im Auffängerkreis als Funktion der
Beschleunigungsspannung 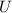 . Aus dem Messergebnis (siehe Abb. 8.8) wird
ersichtlich, dass der Auffängerstrom Maxima durchläuft, die von mehr oder weniger
scharfen Einbrüchen gefolgt sind. Die Maxima sind gleichmässig verteilt mit einem
Abstand von jeweils 4.86 V.
. Aus dem Messergebnis (siehe Abb. 8.8) wird
ersichtlich, dass der Auffängerstrom Maxima durchläuft, die von mehr oder weniger
scharfen Einbrüchen gefolgt sind. Die Maxima sind gleichmässig verteilt mit einem
Abstand von jeweils 4.86 V.
Die Interpretation für das erhaltene Messresultat ist folgende: Die beschleunigten
Elektronen stossen mit den Quecksilberatomen zusammen. Wenn die kinetische
Energie 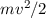 des Elektrons 4.86 eV übersteigt, werden inelastische Stösse
möglich. Dabei handelt es sich aber um besondere inelastische Stösse: Der
Energieverlust des Elektrons beträgt jedes Mal ziemlich genau 4.86 eV. Da das
Massenverhältnis der Stosspartner sehr klein ist (Elektronenmasse
des Elektrons 4.86 eV übersteigt, werden inelastische Stösse
möglich. Dabei handelt es sich aber um besondere inelastische Stösse: Der
Energieverlust des Elektrons beträgt jedes Mal ziemlich genau 4.86 eV. Da das
Massenverhältnis der Stosspartner sehr klein ist (Elektronenmasse 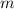 / Masse
Quecksilberatom
/ Masse
Quecksilberatom 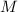 =
= 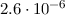 ), wird nach dem Impulserhaltungssatz nur
ein sehr kleiner Bruchteil (Grössenordnung
), wird nach dem Impulserhaltungssatz nur
ein sehr kleiner Bruchteil (Grössenordnung 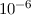 ) der kinetischen Energie
des Elektrons in Form von kinetischer Energie auf das Quecksilberatom
übertragen. Beinahe der gesamte Energieverlust des Stosselektrons wird in der
Elektronenhülle des Quecksilberatoms gespeichert. Die kinetische Energie
des Elektrons nach dem inelastischen Stoss ist deshalb annähernd gegeben
durch
) der kinetischen Energie
des Elektrons in Form von kinetischer Energie auf das Quecksilberatom
übertragen. Beinahe der gesamte Energieverlust des Stosselektrons wird in der
Elektronenhülle des Quecksilberatoms gespeichert. Die kinetische Energie
des Elektrons nach dem inelastischen Stoss ist deshalb annähernd gegeben
durch

wobei 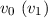 die Geschwindigkeit vor (nach) dem Stoss ist. Dabei haben wir die
Approximation
die Geschwindigkeit vor (nach) dem Stoss ist. Dabei haben wir die
Approximation 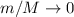 vorgenommen, was nach den oben aufgeführten
Betrachtungen gerechtfertigt ist. Ausserdem wird die thermische Geschwindigkeit der
Quecksilberatome und die Geschwindigkeitsverteilung der aus der Kathode
austretenden Elektronen vernachlässigt.
vorgenommen, was nach den oben aufgeführten
Betrachtungen gerechtfertigt ist. Ausserdem wird die thermische Geschwindigkeit der
Quecksilberatome und die Geschwindigkeitsverteilung der aus der Kathode
austretenden Elektronen vernachlässigt.
Wir gehen noch etwas genauer auf die charakteristische Form der Messkurve ein. Der
erste Abfall des Auffängerstroms wird bei der Beschleunigungsspannung
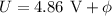 beginnen, wobei
beginnen, wobei 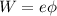 die Austrittsarbeit der Elektronen aus
der Kathode ist. Das Elektron wird in diesem Fall gerade noch einen inelastischen
Stoss machen können und danach still stehen. Wenn die kinetische Energie des
Elektrons nach dem Stoss mehr als 0.5 V beträgt, so vermag es noch gegen die
Gegenspannung von 0.5 V anzulaufen und trägt zum Auffängerstrom bei. Folglich
wird bis zu einer Beschleunigungsspannung von
die Austrittsarbeit der Elektronen aus
der Kathode ist. Das Elektron wird in diesem Fall gerade noch einen inelastischen
Stoss machen können und danach still stehen. Wenn die kinetische Energie des
Elektrons nach dem Stoss mehr als 0.5 V beträgt, so vermag es noch gegen die
Gegenspannung von 0.5 V anzulaufen und trägt zum Auffängerstrom bei. Folglich
wird bis zu einer Beschleunigungsspannung von 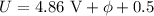 V der
Auffängerstrom sinken und beim Überschreiten dieser Spannung wieder ansteigen. Bei
weiterer Steigerung der Beschleunigungsspannung vermag das Elektron noch einen
zweiten, dritten, vierten ... inelastischen Zusammenstoss ausführen. Da es jedes Mal
die Energie von 4.86 eV verliert folgen die Maxima bzw. Abfälle der
V der
Auffängerstrom sinken und beim Überschreiten dieser Spannung wieder ansteigen. Bei
weiterer Steigerung der Beschleunigungsspannung vermag das Elektron noch einen
zweiten, dritten, vierten ... inelastischen Zusammenstoss ausführen. Da es jedes Mal
die Energie von 4.86 eV verliert folgen die Maxima bzw. Abfälle der 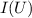 -Kurve in
Abständen von 4.86 V aufeinander.
-Kurve in
Abständen von 4.86 V aufeinander.
Wir schliessen aus diesen Beobachtungen, dass die Elektronenhülle eines
Quecksilberatoms Energie nur in diskreten Quanten von 4.86 eV aufnehmen kann.
Dies ist ein weiterer unabhängiger Hinweis auf das Vorhandensein von diskreten
Energieniveaus in Atomen. In diesem Experiment wird das Quecksilberatom aus dem
Grundzustand in einen angeregten Zustand gehoben, dessen Energie um 4.86
eV höher liegt. Tatsächlich findet man auch eine entsprechende Linie im
optischen Spektrum des Quecksilberatoms bei 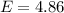 eV bzw.
eV bzw. 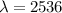 Å .
Å .
Es bleibt jetzt noch die Frage zu klären, was mit dieser Energie geschieht, die in der
Elektronenhülle des gestossenen Quecksilberatoms gespeichert ist. Es zeigt sich, dass
die Quecksilberatome nicht lange in diesem angeregten Zustand bleiben,
sondern innerhalb einer Zeit von ungefähr 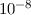 s unter Emission eines
Photons der Energie
s unter Emission eines
Photons der Energie 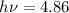 eV in den Grundzustand zurückfallen. Die
Wellenlänge des emittierten Lichts ist gegeben durch
eV in den Grundzustand zurückfallen. Die
Wellenlänge des emittierten Lichts ist gegeben durch 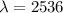 Å . Diese
Strahlung kann im Franck-Hertz-Experiment ebenfalls direkt beobachtet
werden.
Å . Diese
Strahlung kann im Franck-Hertz-Experiment ebenfalls direkt beobachtet
werden.
Bei einer verfeinerten Messanordnung erhält man mehrere Maxima und Minima
in der 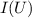 -Messkurve. Es zeigt sich also auch im Stossexperiment die
Tatsache, dass das Quecksilberatom viele angeregte Zustände, d.h. viele
diskrete Energieniveaus besitzt. Es kann auch vorkommen, dass ein Atom durch
einen ersten Elektronenstoss in ein langlebiges, ein sogenanntes metastabiles
Energieniveau gehoben wird. Bevor es dann in den Grundzustand zurückfällt,
kann es durch einen zweiten Stoss in ein noch höhere Energieniveau gehoben
werden.
-Messkurve. Es zeigt sich also auch im Stossexperiment die
Tatsache, dass das Quecksilberatom viele angeregte Zustände, d.h. viele
diskrete Energieniveaus besitzt. Es kann auch vorkommen, dass ein Atom durch
einen ersten Elektronenstoss in ein langlebiges, ein sogenanntes metastabiles
Energieniveau gehoben wird. Bevor es dann in den Grundzustand zurückfällt,
kann es durch einen zweiten Stoss in ein noch höhere Energieniveau gehoben
werden.
Die Absorption und Emission von elektromagnetischer Strahlung durch
Atome werden durch die sogenannten Einstein-Koeffizienten beschrieben.
Im thermischen Gleichgewicht erlauben sie eine alternative Herleitung des
Planckschen Strahlungsgesetzes (5.22), das wir bereits in Kapitel 5 kennengelernt
haben.
Wir betrachten 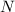 Atome im thermischen Gleichgewicht mit einem
elektromagnetischen Strahlungsfeld der spektralen Energiedichte
Atome im thermischen Gleichgewicht mit einem
elektromagnetischen Strahlungsfeld der spektralen Energiedichte 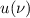 bei einer
Temperatur
bei einer
Temperatur 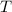 . Des Weiteren betrachten wir Atome mit diskreten Energieniveaus,
wie wir sie in diesem Kapitel kennen gelernt haben. Betrachten wir nun vereinfachend
nur zwei dieser Energieniveaus
. Des Weiteren betrachten wir Atome mit diskreten Energieniveaus,
wie wir sie in diesem Kapitel kennen gelernt haben. Betrachten wir nun vereinfachend
nur zwei dieser Energieniveaus 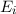 und
und 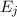 , so gibt es nach Einstein drei
verschiedene physikalische Prozesse, die für einen Übergang zwischen diesen Niveaus
verantwortlich sind (siehe Abb. 8.9):
, so gibt es nach Einstein drei
verschiedene physikalische Prozesse, die für einen Übergang zwischen diesen Niveaus
verantwortlich sind (siehe Abb. 8.9):
- Durch Absorption eines Photons der Energie
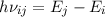 aus dem
elektromagnetischen Feld wird das Atom vom tieferen Energieniveau
aus dem
elektromagnetischen Feld wird das Atom vom tieferen Energieniveau 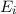 ins höhere Energieniveau
ins höhere Energieniveau 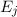 angehoben.
angehoben.
- Es ist möglich, dass ein Atom im Energieniveau
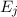 nach einer
gewissen Zeit (mittlere Lebensdauer des Energieniveaus) spontan unter
Emission eines Photons der Energie
nach einer
gewissen Zeit (mittlere Lebensdauer des Energieniveaus) spontan unter
Emission eines Photons der Energie 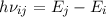 ins tiefer liegende
Energieniveau
ins tiefer liegende
Energieniveau 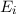 fällt. Dementsprechend wird dieser Vorgang spontane
Emission genannt.
fällt. Dementsprechend wird dieser Vorgang spontane
Emission genannt.
- Bei der stimulierten Emission wird der Übergang des Atoms von
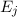 nach
nach 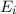 durch ein Photon der Energie
durch ein Photon der Energie 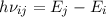 aus dem
elektromagnetischen Feld eingeleitet oder wie es der Name sagt stimuliert.
Dabei wird ein weiteres Photon der Energie
aus dem
elektromagnetischen Feld eingeleitet oder wie es der Name sagt stimuliert.
Dabei wird ein weiteres Photon der Energie 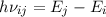 ausgesendet.
Es sei hier bemerkt, dass die stimulierte Emission in Lasern zur Erzeugung
von kohärentem Licht eingesetzt wird.
ausgesendet.
Es sei hier bemerkt, dass die stimulierte Emission in Lasern zur Erzeugung
von kohärentem Licht eingesetzt wird.
Wir nehmen nun an, dass sich 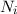 Atome im Zustand
Atome im Zustand 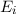 und
und 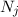 Atome im
Zustand
Atome im
Zustand 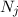 befinden, wobei gilt
befinden, wobei gilt 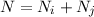 . Wir betrachten die Übergänge von
. Wir betrachten die Übergänge von
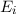 nach
nach 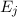 und
und 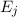 nach
nach 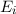 getrennt:
getrennt:
- Die Anzahl
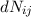 der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte
der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte 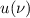 in einem
Zeitintervall
in einem
Zeitintervall 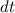 durch Absorption eines Photons von
durch Absorption eines Photons von 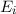 nach
nach 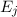 übergehen,
ist gegeben durch
übergehen,
ist gegeben durch
wobei 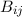 der Einsteinsche B-Koeffizient ist und für die Wahrscheinlichkeit
steht, dass ein Atom ein Photon der Frequenz
der Einsteinsche B-Koeffizient ist und für die Wahrscheinlichkeit
steht, dass ein Atom ein Photon der Frequenz 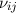 absorbiert.
absorbiert.
- Die Anzahl
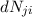 der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte
der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte 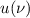 im Zeitintervall
im Zeitintervall
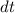 durch spontane oder stimulierte Emission eines Photons von
durch spontane oder stimulierte Emission eines Photons von 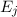 nach
nach 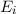 übergehen, ist gegeben durch
übergehen, ist gegeben durch
Dabei ist 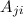 der Einsteinsche A-Koeffizient und steht für die Wahrscheinlichkeit,
dass ein Atom spontan ein Photon der Frequenz
der Einsteinsche A-Koeffizient und steht für die Wahrscheinlichkeit,
dass ein Atom spontan ein Photon der Frequenz 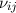 emittiert.
emittiert. 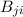 ist ein
weiterer Einsteinscher B-Koeffizient und steht für die Wahrscheinlichkeit,
dass ein Atom durch Wechselwirkung mit einem Photon der Frequenz
ist ein
weiterer Einsteinscher B-Koeffizient und steht für die Wahrscheinlichkeit,
dass ein Atom durch Wechselwirkung mit einem Photon der Frequenz
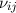 zur Emission eines weiteren Photons der Frequenz
zur Emission eines weiteren Photons der Frequenz 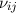 stimuliert
wird.
stimuliert
wird.
Aus (8.53) und (8.54) ergeben sich die Differentialgleichungen für den zeitlichen
Verlauf der Anzahl Atome 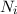 und
und 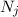 in den Zuständen
in den Zuständen 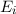 und
und 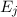 . Die
Änderung
. Die
Änderung 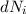 pro Zeitintervall
pro Zeitintervall  der Anzahl Atome im Zustand
der Anzahl Atome im Zustand 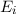 ergibt sich
aus der Differenz zwischen der Anzahl Atome
ergibt sich
aus der Differenz zwischen der Anzahl Atome 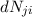 , die im Zeitintervall
, die im Zeitintervall 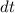 von
von
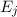 nach
nach 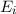 übergehen und der Anzahl Atome
übergehen und der Anzahl Atome 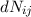 , die im Zeitintervall
, die im Zeitintervall 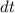 von
von
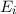 nach
nach 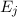 übergehen
übergehen
Analog ergibt sich die Änderung 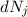 pro Zeitintervall
pro Zeitintervall 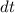 der Anzahl Atome im
Zustand
der Anzahl Atome im
Zustand 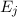 aus der Differenz zwischen der Anzahl Atome
aus der Differenz zwischen der Anzahl Atome 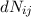 , die im
Zeitintervall
, die im
Zeitintervall 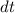 von
von  nach
nach 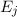 übergehen und der Anzahl Atome
übergehen und der Anzahl Atome  , die im
Zeitintervall
, die im
Zeitintervall 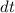 von
von 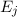 nach
nach 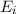 übergehen
übergehen
Einsetzen von (8.53) und (8.54) liefert die folgenden Differentialgleichungen
Im thermischen Gleichgewicht streben die Anzahl Atome 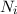 und
und 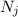 in den
Zuständen
in den
Zuständen 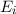 und
und 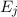 gegen einen konstanten Wert (siehe Abb. 8.10), d.h. die
Ableitungen
gegen einen konstanten Wert (siehe Abb. 8.10), d.h. die
Ableitungen 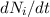 und
und 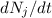 verschwinden.
verschwinden.
Daraus folgt
Diese Gleichung ist gleichbedeutend mit der Aussage, dass im thermischen
Gleichgewicht die Anzahl Übergänge von 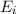 nach
nach 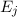 im Zeitintervall
im Zeitintervall 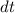 identisch
mit den Anzahl Übergängen im Zeitintervall
identisch
mit den Anzahl Übergängen im Zeitintervall 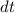 von
von 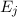 nach
nach 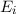 ist, d.h. es
gilt
ist, d.h. es
gilt
Aus (8.59) ergibt sich für die spektrale Energiedichte 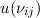 der folgende
Ausdruck
der folgende
Ausdruck
Wir nehmen an, dass die Anzahl der Atome 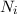 und
und 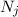 in den Zuständen
in den Zuständen 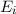 und
und
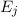 im thermischen Gleichgewicht durch die klassische Maxwell-Boltzmann-Verteilung
gegeben ist
im thermischen Gleichgewicht durch die klassische Maxwell-Boltzmann-Verteilung
gegeben ist
wobei 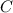 eine Konstante ist. Damit folgt für das Verhältnis der Zahl der Atome
eine Konstante ist. Damit folgt für das Verhältnis der Zahl der Atome 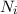 im Zustand
im Zustand 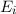 zur Zahl der Atome
zur Zahl der Atome 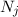 im Zustand
im Zustand 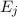
Einsetzen in (8.61) ergibt
Für 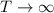 muss gelten
muss gelten 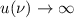 . Daraus folgt, dass die beiden B-Koeffizien-ten
identisch sein müssen
. Daraus folgt, dass die beiden B-Koeffizien-ten
identisch sein müssen
D.h. die Wahrscheinlichkeiten für Absorption und stimulierte Emission sind gleich.
Damit ergibt sich für die spektrale Energiedichte 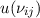
Für sehr kleine Frequenzen, d.h. 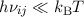 gilt das Rayleigh-Jeans-Gesetz
gilt das Rayleigh-Jeans-Gesetz
Entwickeln wir nun (8.67) für kleine Frequenzen (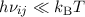 ) dann erhalten
wir
) dann erhalten
wir
Der Vergleich mit dem Rayleigh-Jeans-Gesetz (8.68) liefert für das Verhältnis der
Einstein-Koeffizienten
Mit anderen Worten die Wahrscheinlichkeiten für spontane Emission und Absorption
sind proportional zueinander. Einsetzen in (8.67) liefert nun das folgende
Resultat
Dies ist das Plancksche Strahlungsgesetz (5.22), das wir bereits in Kapitel 5
kennengelernt haben, hergeleitet aus den Prozessen der Absorption und Emission
von elektromagnetischer Strahlung in einem Atom der Übergangsfrequenz
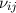 .
.
- Betrachtet man Emissions- oder Absorptionsspektren von Atomen, so
beobachtet man diskrete Linienspektren, was darauf hindeutet, dass
Elektronen in einem Atom mit bestimmten diskreten Energiewerten an
den Atomkern gebunden sind. Neben Linienspektren kommen in der Natur
auch kontinuierliche Spektren (Festkörper oder Gase) oder Bandspektren
(molekulare Gase) vor.
Diese Beobachtung kann mit Methoden der klassischen Physik nicht
erklärt werden. Klassische Theorien würden beliebige Elektronenenergien
und somit kontinuierliche Spektren vorhersagen, zudem versagen sie bei
der Erklärung der Stabilität von Atomen.
Als erster Ansatzpunkt zur Erklärung der Spektren von Atomen gilt
das Ritzsche Kombinationsprinzip, das besagt, dass die Frequenz  jeder Spektrallinie eines Atoms als Differenz zwischen zwei sogenannten
Spektraltermen
jeder Spektrallinie eines Atoms als Differenz zwischen zwei sogenannten
Spektraltermen 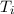 und
und 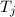 darstellen lässt und dass jede Atomsorte
einen für sie charakteristischen Satz von Spektraltermen
darstellen lässt und dass jede Atomsorte
einen für sie charakteristischen Satz von Spektraltermen 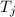 besitzt.
besitzt.
- Das Wasserstoffspektrum besteht aus einer Vielzahl von Serien, wie z.B. die
Balmer-Serie im sichtbaren Bereich. Die Gesamtheit aller Serien wird durch die
Rydberg-Formel beschrieben
wobei die ganzen Zahlen 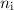 und
und 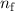 , die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und
, die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und 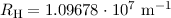 die Rydberg-Konstante ist.
die Rydberg-Konstante ist.
- Das erste einfache Modell zur Beschreibung des Spektrum des Wasserstoffatoms
ist das Bohrsche Atommodell. Einerseits ging Bohr vom Rutherfordschen
Atommodell aus, indem er annahm, dass sich im Wasserstoffatom das negativ
geladene Elektron auf einer Kreisbahn um den positiv geladenen Kern
bewegt. Andererseits formulierte er ausgehend von den experimentellen
Erkenntnissen über atomare Spektren drei Postulate. Daraus erhielt er folgende
Resultate:
- Rydberkonstante
- Bahnradius
wobei der kleinste Bahnradius 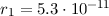 m Bohrscher Radius
genannt wird und üblicherweise mit
m Bohrscher Radius
genannt wird und üblicherweise mit 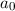 bezeichnet wird.
bezeichnet wird.
- Bahndrehimpuls
- Die Resultate des Bohrschen Atommodells lassen sich auf wasserstoffähnliche
Systeme wie Ionen mit einem Elektron, das sich um einen Kern mit
Kernladungszahl
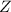 bewegt, erweitern. Berücksichtigt man zudem noch die
Bewegung des Kerns, so ergibt sich zur Beschreibung der Spektren von
wasserstoffähnlichen Systemen folgende allgemeine Formel
bewegt, erweitern. Berücksichtigt man zudem noch die
Bewegung des Kerns, so ergibt sich zur Beschreibung der Spektren von
wasserstoffähnlichen Systemen folgende allgemeine Formel
wobei 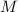 die Kernmasse bezeichnet.
die Kernmasse bezeichnet.
- Aufgrund von beobachteten Feinstrukturen im Wasserstoffspektrum,
postulierte Sommerfeld eine Erweiterung des Bohrschen Atommodells. Unter
Berücksichtigung, dass für Elektronen neben Kreisbahnen auch Ellipsenbahnen
möglich sind sowie der Relativitätstheorie, erhielt er für die Energiewerte
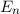 der Elektronen
der Elektronen
Dabei ist 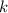 eine zweite Quantenzahl und
eine zweite Quantenzahl und 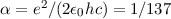 die
Feinstrukturkonstante.
die
Feinstrukturkonstante.
- Das Bohr-Sommerfeld-Modell beschreibt einige grundlegende Eigenschaften des
Wasserstoffatoms in guter Näherung. Es weist aber seine Grenzen auf, wie
z.B. dass mit dem Modell keine korrekten Vorhersagen für Atome mit mehreren
Elektronen möglich sind. Eine genaue Beschreibung ist nur in einem rein
quantenmechanischen Modell möglich.
- Atome, welche sich annähernd durch das Bohr-Sommerfeld-Modell beschreiben
lassen, sind Rydberg-Atome. Das sind Atome, bei denen sich ein Elektron
in einem Zustand mit einer sehr grossen Hauptquantenzahl
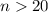 befindet und die ein wichtiger Bestandteil der Grundlagenforschung
sind.
befindet und die ein wichtiger Bestandteil der Grundlagenforschung
sind.
- Unabhängig von optischer Spektroskopie wurde die Existenz von diskreten
Energieniveaus im Atom durch das Franck-Hertz-Experiment nachgewiesen: Im
Experiment treffen beschleunigte Elektronen auf Quecksilberatome und es zeigt
sich, dass diese Atome nur Energie in diskreten Quanten aufnehmen
können.
- Betrachtet man zwei Energieniveaus
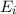 und
und 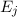 eines Atoms, so gibt es nach
Einstein die drei physikalischen Prozesse Absorption, spontane und stimulierte
Emission, die für einen Übergang zwischen diesen Niveaus verantwortlich sind.
Diese Prozesse werden durch sogenannte Einstein-Koeffizienten beschrieben. Im
thermischen Gleichgewicht erlauben sie eine alternative Herleitung des
Planckschen Strahlungsgesetzes.
eines Atoms, so gibt es nach
Einstein die drei physikalischen Prozesse Absorption, spontane und stimulierte
Emission, die für einen Übergang zwischen diesen Niveaus verantwortlich sind.
Diese Prozesse werden durch sogenannte Einstein-Koeffizienten beschrieben. Im
thermischen Gleichgewicht erlauben sie eine alternative Herleitung des
Planckschen Strahlungsgesetzes.
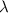
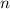 ebenfalls eine Funktion der Wellenlänge
ist (Dispersion). Gemessen werden solche Spektren mit Hilfe von
Beugungs-Gittern.
ebenfalls eine Funktion der Wellenlänge
ist (Dispersion). Gemessen werden solche Spektren mit Hilfe von
Beugungs-Gittern.

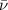
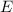
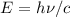 wird in der Einheit eV (Elektronenvolt) angegeben.
wird in der Einheit eV (Elektronenvolt) angegeben.


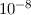 s. Dies
steht jedoch klar im Widerspruch mit der Tatsache, dass Atome (in ihrem
Grundzustand) stabil sind und dass Atome Licht bei diskreten Frequenzen
abstrahlen und kein kontinuierliches Spektrum haben (siehe Abschnitt
s. Dies
steht jedoch klar im Widerspruch mit der Tatsache, dass Atome (in ihrem
Grundzustand) stabil sind und dass Atome Licht bei diskreten Frequenzen
abstrahlen und kein kontinuierliches Spektrum haben (siehe Abschnitt 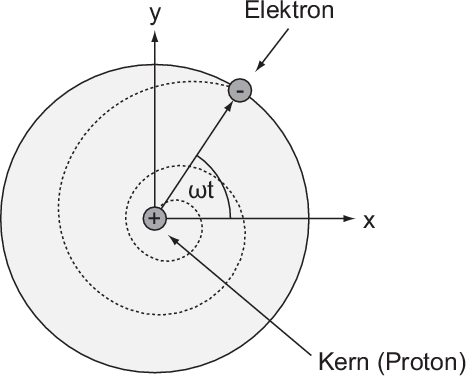
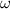 . Nach der klassischen
Vorstellung würde das Elektron auf seiner Bahn kinetische Energie verlieren und
auf einer Spiralbahn in den Kern stürzen.
. Nach der klassischen
Vorstellung würde das Elektron auf seiner Bahn kinetische Energie verlieren und
auf einer Spiralbahn in den Kern stürzen. jeder Spektrallinie eines Atoms lässt sich darstellen als die Differenz
zwischen zwei sogenannten
jeder Spektrallinie eines Atoms lässt sich darstellen als die Differenz
zwischen zwei sogenannten 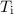 und
und 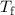

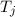 .
.
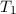 ,
, 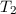 und
und 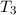 . Demzufolge lässt es folgende drei Frequenzen zu
. Demzufolge lässt es folgende drei Frequenzen zu

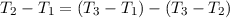 folgt, dass zwischen den drei Frequenzen die
folgende Beziehung gelten muss
folgt, dass zwischen den drei Frequenzen die
folgende Beziehung gelten muss

 ,
,  und
und 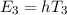 und kann unter Emission eines Photons von
einem Niveau in ein anderes übergehen, wobei die Energie
und kann unter Emission eines Photons von
einem Niveau in ein anderes übergehen, wobei die Energie 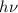 des Photons der
Differenz zwischen den beiden Energieniveaus entspricht (siehe Abb.
des Photons der
Differenz zwischen den beiden Energieniveaus entspricht (siehe Abb. 

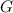 ein empirisch gefundener Zahlenwert ist.
ein empirisch gefundener Zahlenwert ist. 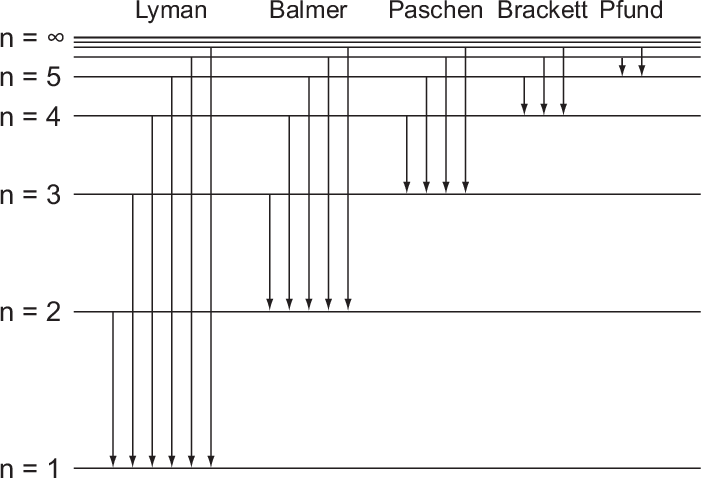

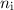 und
und 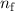 , die sogenannten
, die sogenannten 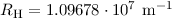 die
die
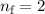 .
Die wichtigsten Serien beim Wasserstoffatom sind neben der Balmer-Serie die
Lyman-, Paschen-, Brackett und Pfund-Serie (siehe Tab.
.
Die wichtigsten Serien beim Wasserstoffatom sind neben der Balmer-Serie die
Lyman-, Paschen-, Brackett und Pfund-Serie (siehe Tab. 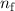
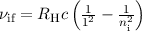
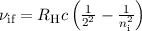
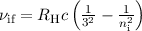
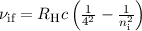
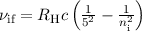
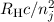 gerade den Spektraltermen
gerade den Spektraltermen
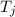 entspricht. Die Terme
entspricht. Die Terme 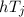 können somit als mögliche Energieniveaus des
Elektrons im Atom interpretiert werden für die das Bohrsche Atommodell eine erste
Erklärung lieferte.
können somit als mögliche Energieniveaus des
Elektrons im Atom interpretiert werden für die das Bohrsche Atommodell eine erste
Erklärung lieferte.
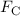 zwischen Elektron und Kern, und der
Zentripetalkraft
zwischen Elektron und Kern, und der
Zentripetalkraft 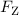 , die das Elektrons mit Masse
, die das Elektrons mit Masse 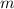 und Geschwindigkeit
und Geschwindigkeit  auf
seiner Bahn mit Radius
auf
seiner Bahn mit Radius  wahrnimmt
wahrnimmt

 des Elektrons,
um bei einem gegebenem Bahnradius
des Elektrons,
um bei einem gegebenem Bahnradius  zu einer stabilen Kreisbahn zu
führen
zu einer stabilen Kreisbahn zu
führen


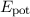 entspricht der Arbeit, die man gewinnt, wenn man das
Elektron aus dem Unendlichen unter Einwirkung der Coulomb-Kraft
entspricht der Arbeit, die man gewinnt, wenn man das
Elektron aus dem Unendlichen unter Einwirkung der Coulomb-Kraft 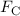 zum
Abstand
zum
Abstand  vom Kern bringt
vom Kern bringt

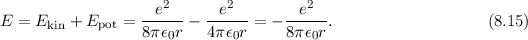
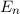 , die Energieterme des Atoms, erlaubt. Wie bei Rydberg wird
, die Energieterme des Atoms, erlaubt. Wie bei Rydberg wird 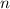 Hauptquantenzahl genannt.
Hauptquantenzahl genannt.
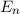 (also grösserem
(also grösserem  ) auf eine Bahn mit grösserer Bindungsenergie
) auf eine Bahn mit grösserer Bindungsenergie 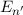 (kleinerem
(kleinerem  ) zu gelangen. Für das bei diesem Übergang emittierte Photon gilt
der folgende Zusammenhang
) zu gelangen. Für das bei diesem Übergang emittierte Photon gilt
der folgende Zusammenhang


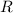 die Rydberg-Konstante bezeichnet. Das Minuszeichen zeigt an, dass
es sich dabei um Bindungsenergien handelt.
die Rydberg-Konstante bezeichnet. Das Minuszeichen zeigt an, dass
es sich dabei um Bindungsenergien handelt.
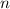 ) gehen die Gesetze der
Quantenmechanik in diejenige der klassischen Mechanik über. Dieses Prinzip
wird
) gehen die Gesetze der
Quantenmechanik in diejenige der klassischen Mechanik über. Dieses Prinzip
wird 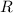 in (
in (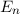 des Wasserstoffatoms durch atomaren Grössen
ausdrücken.
des Wasserstoffatoms durch atomaren Grössen
ausdrücken.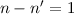 , bei grossem
, bei grossem 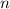 .
Aus (
.
Aus (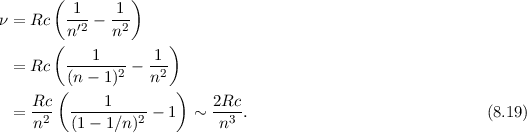
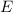 in (
in (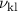 aus. Mit
aus. Mit 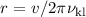 und (
und (
 ergibt
ergibt

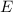 den Ausdruck
den Ausdruck

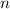 die Gesetze der Quantenmechanik in diejenige der klassischen Mechanik
übergehen und können deshalb
die Gesetze der Quantenmechanik in diejenige der klassischen Mechanik
übergehen und können deshalb 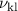 in (
in (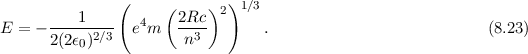
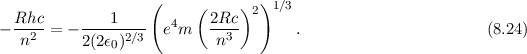
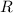 den folgenden Ausdruck
den folgenden Ausdruck

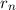 des Elektrons
im Wasserstoffatom. Gleichsetzen von (
des Elektrons
im Wasserstoffatom. Gleichsetzen von (
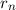
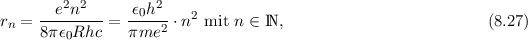
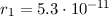 m
m 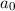 bezeichnet wird.
bezeichnet wird.
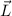 des Elektrons
des Elektrons
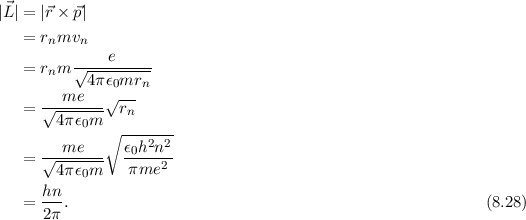
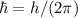 ergibt sich
ergibt sich

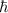 .
.


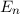 erlaubt, die
Bewegung auf diesen Bahnen erfolgt strahlungslos, jedoch kann Strahlung beim
Übergang eines Elektrons von einer Bahn auf eine andere emittiert oder absorbiert
werden, für diesen Übergang gilt
erlaubt, die
Bewegung auf diesen Bahnen erfolgt strahlungslos, jedoch kann Strahlung beim
Übergang eines Elektrons von einer Bahn auf eine andere emittiert oder absorbiert
werden, für diesen Übergang gilt 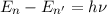 und die Energieniveaus sind nach
Rydberg gegeben durch
und die Energieniveaus sind nach
Rydberg gegeben durch 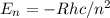 .
.
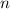 ) die
Gesetze der Quantenmechanik in diejenige der klassischen Mechanik übergehen und
der daraus resultierenden Grenzbetrachtung: Gleichsetzen der Umlauffrequenz auf
den klassischen Kreisbahnen mit der (quantenmechanischen) Frequenz der
emittierten oder absorbierten Strahlung für hohe
) die
Gesetze der Quantenmechanik in diejenige der klassischen Mechanik übergehen und
der daraus resultierenden Grenzbetrachtung: Gleichsetzen der Umlauffrequenz auf
den klassischen Kreisbahnen mit der (quantenmechanischen) Frequenz der
emittierten oder absorbierten Strahlung für hohe 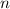 .
.
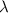 des Elektrons auf seiner klassischen Bahn um den Atomkern
des Elektrons auf seiner klassischen Bahn um den Atomkern


 erlaubt für
die die Materiewelle des Elektrons mit sich selbst konstruktiv interferiert, d.h. die
Länge der Umlaufbahn
erlaubt für
die die Materiewelle des Elektrons mit sich selbst konstruktiv interferiert, d.h. die
Länge der Umlaufbahn 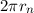 muss einem ganzzahligen Vielfachen der de
Broglie-Wellenlänge
muss einem ganzzahligen Vielfachen der de
Broglie-Wellenlänge 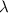 des Elektrons entsprechen. Oder in anderen Worten
ausgedrückt: Die Materiewelle muss nach einer Umdrehung wieder auf sich selber
treffen. Demzufolge lautet die Gleichung zur Bestimmung der Bahnradien
des Elektrons entsprechen. Oder in anderen Worten
ausgedrückt: Die Materiewelle muss nach einer Umdrehung wieder auf sich selber
treffen. Demzufolge lautet die Gleichung zur Bestimmung der Bahnradien 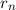 (Interferenzbedingung)
(Interferenzbedingung)

 des Elektrons
des Elektrons

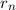 ist also quadratisch in der Hauptquantenzahl
ist also quadratisch in der Hauptquantenzahl 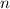 des Elektrons
im Wasserstoffatom.
des Elektrons
im Wasserstoffatom.
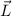 zu:
zu: 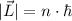 .
.
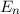 des Elektrons im Wasserstoffatom ergibt sich mit (
des Elektrons im Wasserstoffatom ergibt sich mit (

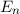 umgekehrt proportional
ist zum Quadrat der Hauptquantenzahl
umgekehrt proportional
ist zum Quadrat der Hauptquantenzahl 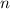 . Dieses Verhalten ist charakteristisch für
die
. Dieses Verhalten ist charakteristisch für
die  -Abhängigkeit des Coulomb-Potentials.
-Abhängigkeit des Coulomb-Potentials.
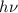 an ein
Elektron weiter, welches dadurch von einem tiefer liegenden Energieniveau
in ein höher liegendes Energieniveau wechselt.
an ein
Elektron weiter, welches dadurch von einem tiefer liegenden Energieniveau
in ein höher liegendes Energieniveau wechselt.
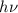 in ein tiefer
liegendes Energieniveau. Das Elektron muss zuvor durch Energiezufuhr
auf dieses höhere Energieniveau gebracht worden sein.
in ein tiefer
liegendes Energieniveau. Das Elektron muss zuvor durch Energiezufuhr
auf dieses höhere Energieniveau gebracht worden sein.
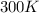 ) ist nur der Grundzustand
des Wasserstoffatoms (
) ist nur der Grundzustand
des Wasserstoffatoms (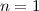 ) besetzt. Deshalb kann man bei normalen
Temperaturen nur die Lyman-Serie in Absorption beobachten. Bei höheren
Temperaturen, wie sie z.B. in der Atmosphäre von Sternen vorkommen,
ist auch der erste angeregte Zustand des Wasserstoffs (
) besetzt. Deshalb kann man bei normalen
Temperaturen nur die Lyman-Serie in Absorption beobachten. Bei höheren
Temperaturen, wie sie z.B. in der Atmosphäre von Sternen vorkommen,
ist auch der erste angeregte Zustand des Wasserstoffs (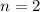 ) besetzt
und weitere Spektrallinien können beobachtet werden.
) besetzt
und weitere Spektrallinien können beobachtet werden.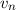 auf einer Kreisbahn mit Radius
auf einer Kreisbahn mit Radius 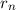 um einen positiv geladenen Kern mit
Kernladungszahl
um einen positiv geladenen Kern mit
Kernladungszahl 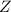 bewegt (z.B. He
bewegt (z.B. He oder Li
oder Li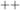 (siehe Abb.
(siehe Abb. 
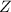 ) mit einer Geschwindigkeit
) mit einer Geschwindigkeit 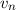 auf einer Kreisbahn mit
Radius
auf einer Kreisbahn mit
Radius 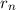 umkreist.
umkreist.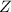

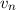 einer stabilen Bahn des Elektrons
einer stabilen Bahn des Elektrons

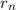 des Elektrons
des Elektrons

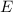 ist nach (
ist nach (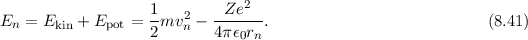

 der emittierten oder absorbierten
Strahlung bei einem Elektronenübergang an. Mit (
der emittierten oder absorbierten
Strahlung bei einem Elektronenübergang an. Mit (
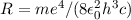 die Rydberg-Konstante ist. Somit erkennen wir, dass die
Bindungsenergie und auch die Energie der emittierten Photonen wie
die Rydberg-Konstante ist. Somit erkennen wir, dass die
Bindungsenergie und auch die Energie der emittierten Photonen wie 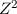 mit der
Kernladungszahl des ionisierten Atoms skaliert. Daher haben Ionen immer deutlich
höhere Übergangsfrequenzen als neutrale Atome.
mit der
Kernladungszahl des ionisierten Atoms skaliert. Daher haben Ionen immer deutlich
höhere Übergangsfrequenzen als neutrale Atome.
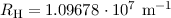 (siehe Abschnitt
(siehe Abschnitt 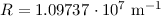 aus (
aus (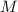 und
und 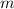 und Abstand
und Abstand  kann aufgefasst werden als die Bewegung eines fiktiven
Teilchens, das den Schwerpunkt im Abstand
kann aufgefasst werden als die Bewegung eines fiktiven
Teilchens, das den Schwerpunkt im Abstand  umläuft und die reduzierte
Masse
umläuft und die reduzierte
Masse 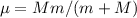 besitzt. Die Masse
besitzt. Die Masse 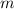 des Elektrons muss also
durch die reduzierte Masse
des Elektrons muss also
durch die reduzierte Masse 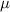 ersetzt werden. Damit erhalten wir für die
korrigierte Rydberg-Konstante, die wir mit
ersetzt werden. Damit erhalten wir für die
korrigierte Rydberg-Konstante, die wir mit 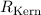 bezeichnen, folgenden
Ausdruck
bezeichnen, folgenden
Ausdruck

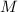 die Protonenmasse einzusetzen. Es ergibt sich
der folgende Wert
die Protonenmasse einzusetzen. Es ergibt sich
der folgende Wert

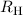 übereinstimmt.
übereinstimmt.
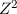 und die Rydberg-Konstante
und die Rydberg-Konstante 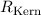 überein
überein

 diverse Serien von Spektrallinien gefunden die durch (
diverse Serien von Spektrallinien gefunden die durch ( -Ion postulierte Sommerfeld um 1915 eine
Erweiterung des Bohrschen Atommodells.
-Ion postulierte Sommerfeld um 1915 eine
Erweiterung des Bohrschen Atommodells.
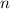 eine
zweite Quantenzahl notwendig. Die Hauptquantenzahl bestimmt weiterhin die
Gesamtenergie
eine
zweite Quantenzahl notwendig. Die Hauptquantenzahl bestimmt weiterhin die
Gesamtenergie 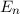 nach der Formel
nach der Formel

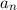 der Ellipse. Zur Festlegung
der kleinen Hauptachse
der Ellipse. Zur Festlegung
der kleinen Hauptachse 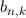 ist nun die neue Quantenzahl
ist nun die neue Quantenzahl 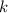 verantwortlich: Der
Betrag des Bahndrehimpulses muss ein Vielfaches von
verantwortlich: Der
Betrag des Bahndrehimpulses muss ein Vielfaches von 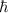 sein
sein

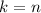 ist, die Ellipsenbahn zu einem
Kreis wird. Zusammenfassend können wir sagen, dass zu jeder Hauptquantenzahl
ist, die Ellipsenbahn zu einem
Kreis wird. Zusammenfassend können wir sagen, dass zu jeder Hauptquantenzahl 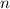 (und damit zur Energie
(und damit zur Energie 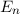 ) eine grosse Hauptachse
) eine grosse Hauptachse 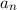 gehört, jedoch
verschiedene kleine Hauptachsen
gehört, jedoch
verschiedene kleine Hauptachsen 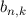 , welche durch die zweite Quantenzahl
, welche durch die zweite Quantenzahl 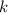 festgelegt werden.
festgelegt werden.
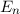 zwar verschiedene Bahnen gehören,
jedoch ist die Zahl der beobachtbaren Linien im Spektrum gleich geblieben, d.h. das
bisherige Modell liefert noch keine Erklärung für die anfangs erwähnte Feinstruktur
in atomaren Spektren. Sommerfeld postulierte 1916 daher eine weitere Erweiterung:
Die Berücksichtigung der bisher vernachlässigten Relativitätstheorie. Dadurch wird
die Masse
zwar verschiedene Bahnen gehören,
jedoch ist die Zahl der beobachtbaren Linien im Spektrum gleich geblieben, d.h. das
bisherige Modell liefert noch keine Erklärung für die anfangs erwähnte Feinstruktur
in atomaren Spektren. Sommerfeld postulierte 1916 daher eine weitere Erweiterung:
Die Berücksichtigung der bisher vernachlässigten Relativitätstheorie. Dadurch wird
die Masse 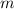 zu einer Grösse die von der Geschwindigkeit abhängt. Ein qualitatives
Verständnis liefert die Anwendung des 2. Keplerschen Gesetzes auf Atome: Zieht man
eine Verbindungslinie zwischen Kern und Elektron so überstreicht diese in gleichen
Zeiten gleich grosse Flächen. Folglich bewegen sich die Elektronen auf ihren
Ellipsenbahnen näher am Kern schneller und sind daher auch schwerer. Dies
führt zu einer Änderung der Bahnform und der Energie: Das Elektron führt
eine Art Rosettenbewegung durch und für die Energie
zu einer Grösse die von der Geschwindigkeit abhängt. Ein qualitatives
Verständnis liefert die Anwendung des 2. Keplerschen Gesetzes auf Atome: Zieht man
eine Verbindungslinie zwischen Kern und Elektron so überstreicht diese in gleichen
Zeiten gleich grosse Flächen. Folglich bewegen sich die Elektronen auf ihren
Ellipsenbahnen näher am Kern schneller und sind daher auch schwerer. Dies
führt zu einer Änderung der Bahnform und der Energie: Das Elektron führt
eine Art Rosettenbewegung durch und für die Energie 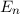 ergibt sich nach
Sommerfeld
ergibt sich nach
Sommerfeld
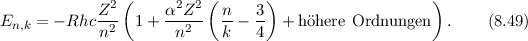
 die
die 
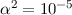 und daher eher
klein.
und daher eher
klein.
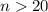 befindet. Solche
Atome werden
befindet. Solche
Atome werden 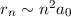 . In Experimenten wurden
bereits Rydberg-Atome mit einem Durchmesser von bis zu
. In Experimenten wurden
bereits Rydberg-Atome mit einem Durchmesser von bis zu 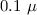 m
erzeugt. Dadurch sind Rydberg-Atome im Vergleich zu einem Atom im
Grundzustand bis
m
erzeugt. Dadurch sind Rydberg-Atome im Vergleich zu einem Atom im
Grundzustand bis 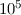 mal grösser.
mal grösser.
 besitzt. Rydberg-Atome
verhalten sich also wie Wasserstoffatome mit hoher Hauptquantenzahl
besitzt. Rydberg-Atome
verhalten sich also wie Wasserstoffatome mit hoher Hauptquantenzahl
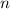 und können durch das Bohr-Sommerfeld-Modell annähernd gut
beschrieben werden.
und können durch das Bohr-Sommerfeld-Modell annähernd gut
beschrieben werden.
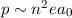 aus
und zeigen daher eine sehr starke Wechselwirkung mit Licht.
aus
und zeigen daher eine sehr starke Wechselwirkung mit Licht.
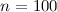 beim wechseln der
Bahn (Verringerung der Hauptquantenzahl
beim wechseln der
Bahn (Verringerung der Hauptquantenzahl 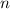 um 1) nach (
um 1) nach ( von
von 
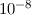 s.
s.
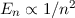 bei grossen
bei grossen  sehr klein wird.
sehr klein wird.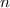 bis zu 350
beobachten. Mit Hilfe von Rydberg-Atome konnte man Grössen wie Energieniveaus
oder Lebensdauern für Quantenzahlen experimentell bestimmen, die bis dahin nur
theoretisch zugänglich waren.
bis zu 350
beobachten. Mit Hilfe von Rydberg-Atome konnte man Grössen wie Energieniveaus
oder Lebensdauern für Quantenzahlen experimentell bestimmen, die bis dahin nur
theoretisch zugänglich waren.
 im Auffängerkreis als Funktion der
Beschleunigungsspannung
im Auffängerkreis als Funktion der
Beschleunigungsspannung 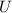 . Aus dem Messergebnis (siehe Abb.
. Aus dem Messergebnis (siehe Abb. 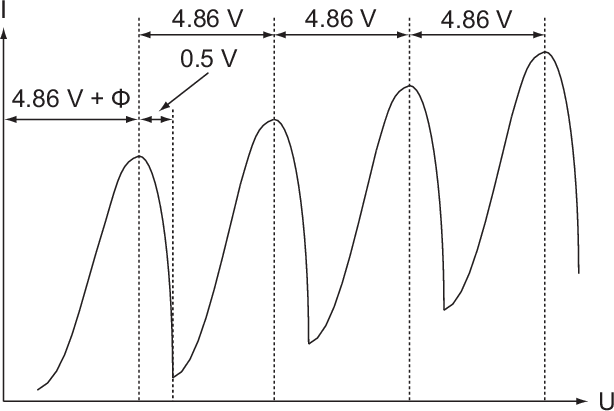
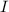 als
Funktion der Beschleunigungsspannung
als
Funktion der Beschleunigungsspannung 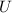 .
.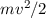 des Elektrons 4.86 eV übersteigt, werden inelastische Stösse
möglich. Dabei handelt es sich aber um besondere inelastische Stösse: Der
Energieverlust des Elektrons beträgt jedes Mal ziemlich genau 4.86 eV. Da das
Massenverhältnis der Stosspartner sehr klein ist (Elektronenmasse
des Elektrons 4.86 eV übersteigt, werden inelastische Stösse
möglich. Dabei handelt es sich aber um besondere inelastische Stösse: Der
Energieverlust des Elektrons beträgt jedes Mal ziemlich genau 4.86 eV. Da das
Massenverhältnis der Stosspartner sehr klein ist (Elektronenmasse 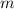 / Masse
Quecksilberatom
/ Masse
Quecksilberatom 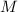 =
= 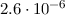 ), wird nach dem Impulserhaltungssatz nur
ein sehr kleiner Bruchteil (Grössenordnung
), wird nach dem Impulserhaltungssatz nur
ein sehr kleiner Bruchteil (Grössenordnung 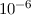 ) der kinetischen Energie
des Elektrons in Form von kinetischer Energie auf das Quecksilberatom
übertragen. Beinahe der gesamte Energieverlust des Stosselektrons wird in der
Elektronenhülle des Quecksilberatoms gespeichert. Die kinetische Energie
des Elektrons nach dem inelastischen Stoss ist deshalb annähernd gegeben
durch
) der kinetischen Energie
des Elektrons in Form von kinetischer Energie auf das Quecksilberatom
übertragen. Beinahe der gesamte Energieverlust des Stosselektrons wird in der
Elektronenhülle des Quecksilberatoms gespeichert. Die kinetische Energie
des Elektrons nach dem inelastischen Stoss ist deshalb annähernd gegeben
durch

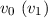 die Geschwindigkeit vor (nach) dem Stoss ist. Dabei haben wir die
Approximation
die Geschwindigkeit vor (nach) dem Stoss ist. Dabei haben wir die
Approximation 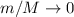 vorgenommen, was nach den oben aufgeführten
Betrachtungen gerechtfertigt ist. Ausserdem wird die thermische Geschwindigkeit der
Quecksilberatome und die Geschwindigkeitsverteilung der aus der Kathode
austretenden Elektronen vernachlässigt.
vorgenommen, was nach den oben aufgeführten
Betrachtungen gerechtfertigt ist. Ausserdem wird die thermische Geschwindigkeit der
Quecksilberatome und die Geschwindigkeitsverteilung der aus der Kathode
austretenden Elektronen vernachlässigt.
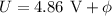 beginnen, wobei
beginnen, wobei 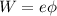 die Austrittsarbeit der Elektronen aus
der Kathode ist. Das Elektron wird in diesem Fall gerade noch einen inelastischen
Stoss machen können und danach still stehen. Wenn die kinetische Energie des
Elektrons nach dem Stoss mehr als 0.5 V beträgt, so vermag es noch gegen die
Gegenspannung von 0.5 V anzulaufen und trägt zum Auffängerstrom bei. Folglich
wird bis zu einer Beschleunigungsspannung von
die Austrittsarbeit der Elektronen aus
der Kathode ist. Das Elektron wird in diesem Fall gerade noch einen inelastischen
Stoss machen können und danach still stehen. Wenn die kinetische Energie des
Elektrons nach dem Stoss mehr als 0.5 V beträgt, so vermag es noch gegen die
Gegenspannung von 0.5 V anzulaufen und trägt zum Auffängerstrom bei. Folglich
wird bis zu einer Beschleunigungsspannung von 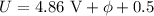 V der
Auffängerstrom sinken und beim Überschreiten dieser Spannung wieder ansteigen. Bei
weiterer Steigerung der Beschleunigungsspannung vermag das Elektron noch einen
zweiten, dritten, vierten ... inelastischen Zusammenstoss ausführen. Da es jedes Mal
die Energie von 4.86 eV verliert folgen die Maxima bzw. Abfälle der
V der
Auffängerstrom sinken und beim Überschreiten dieser Spannung wieder ansteigen. Bei
weiterer Steigerung der Beschleunigungsspannung vermag das Elektron noch einen
zweiten, dritten, vierten ... inelastischen Zusammenstoss ausführen. Da es jedes Mal
die Energie von 4.86 eV verliert folgen die Maxima bzw. Abfälle der 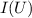 -Kurve in
Abständen von 4.86 V aufeinander.
-Kurve in
Abständen von 4.86 V aufeinander.
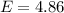 eV bzw.
eV bzw. 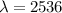 Å .
Å .
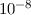 s unter Emission eines
Photons der Energie
s unter Emission eines
Photons der Energie 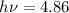 eV in den Grundzustand zurückfallen. Die
Wellenlänge des emittierten Lichts ist gegeben durch
eV in den Grundzustand zurückfallen. Die
Wellenlänge des emittierten Lichts ist gegeben durch 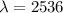 Å . Diese
Strahlung kann im Franck-Hertz-Experiment ebenfalls direkt beobachtet
werden.
Å . Diese
Strahlung kann im Franck-Hertz-Experiment ebenfalls direkt beobachtet
werden.
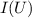 -Messkurve. Es zeigt sich also auch im Stossexperiment die
Tatsache, dass das Quecksilberatom viele angeregte Zustände, d.h. viele
diskrete Energieniveaus besitzt. Es kann auch vorkommen, dass ein Atom durch
einen ersten Elektronenstoss in ein langlebiges, ein sogenanntes
-Messkurve. Es zeigt sich also auch im Stossexperiment die
Tatsache, dass das Quecksilberatom viele angeregte Zustände, d.h. viele
diskrete Energieniveaus besitzt. Es kann auch vorkommen, dass ein Atom durch
einen ersten Elektronenstoss in ein langlebiges, ein sogenanntes 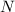 Atome im thermischen Gleichgewicht mit einem
elektromagnetischen Strahlungsfeld der spektralen Energiedichte
Atome im thermischen Gleichgewicht mit einem
elektromagnetischen Strahlungsfeld der spektralen Energiedichte 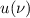 bei einer
Temperatur
bei einer
Temperatur 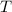 . Des Weiteren betrachten wir Atome mit diskreten Energieniveaus,
wie wir sie in diesem Kapitel kennen gelernt haben. Betrachten wir nun vereinfachend
nur zwei dieser Energieniveaus
. Des Weiteren betrachten wir Atome mit diskreten Energieniveaus,
wie wir sie in diesem Kapitel kennen gelernt haben. Betrachten wir nun vereinfachend
nur zwei dieser Energieniveaus 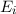 und
und 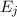 , so gibt es nach Einstein drei
verschiedene physikalische Prozesse, die für einen Übergang zwischen diesen Niveaus
verantwortlich sind (siehe Abb.
, so gibt es nach Einstein drei
verschiedene physikalische Prozesse, die für einen Übergang zwischen diesen Niveaus
verantwortlich sind (siehe Abb. 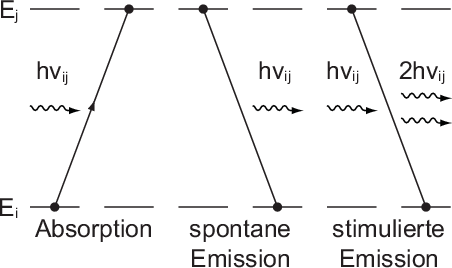
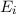 und
und 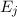 .
.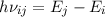 aus dem
elektromagnetischen Feld wird das Atom vom tieferen Energieniveau
aus dem
elektromagnetischen Feld wird das Atom vom tieferen Energieniveau 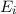 ins höhere Energieniveau
ins höhere Energieniveau 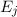 angehoben.
angehoben.
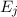 nach einer
gewissen Zeit (mittlere Lebensdauer des Energieniveaus) spontan unter
Emission eines Photons der Energie
nach einer
gewissen Zeit (mittlere Lebensdauer des Energieniveaus) spontan unter
Emission eines Photons der Energie 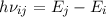 ins tiefer liegende
Energieniveau
ins tiefer liegende
Energieniveau 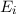 fällt. Dementsprechend wird dieser Vorgang
fällt. Dementsprechend wird dieser Vorgang 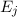 nach
nach 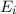 durch ein Photon der Energie
durch ein Photon der Energie 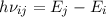 aus dem
elektromagnetischen Feld eingeleitet oder wie es der Name sagt stimuliert.
Dabei wird ein weiteres Photon der Energie
aus dem
elektromagnetischen Feld eingeleitet oder wie es der Name sagt stimuliert.
Dabei wird ein weiteres Photon der Energie 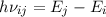 ausgesendet.
Es sei hier bemerkt, dass die stimulierte Emission in Lasern zur Erzeugung
von kohärentem Licht eingesetzt wird.
ausgesendet.
Es sei hier bemerkt, dass die stimulierte Emission in Lasern zur Erzeugung
von kohärentem Licht eingesetzt wird.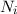 Atome im Zustand
Atome im Zustand 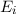 und
und 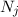 Atome im
Zustand
Atome im
Zustand 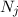 befinden, wobei gilt
befinden, wobei gilt 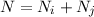 . Wir betrachten die Übergänge von
. Wir betrachten die Übergänge von
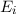 nach
nach 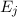 und
und 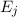 nach
nach 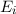 getrennt:
getrennt:
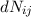 der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte
der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte 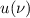 in einem
Zeitintervall
in einem
Zeitintervall 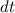 durch Absorption eines Photons von
durch Absorption eines Photons von 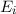 nach
nach 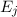 übergehen,
ist gegeben durch
übergehen,
ist gegeben durch 
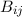 der
der 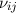 absorbiert.
absorbiert.
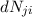 der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte
der Atome, die durch Wechselwirkung mit dem
elektromagnetischen Feld der spektralen Energiedichte 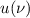 im Zeitintervall
im Zeitintervall
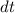 durch spontane oder stimulierte Emission eines Photons von
durch spontane oder stimulierte Emission eines Photons von 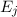 nach
nach 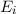 übergehen, ist gegeben durch
übergehen, ist gegeben durch 
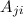 der
der 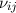 emittiert.
emittiert. 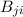 ist ein
weiterer
ist ein
weiterer 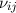 zur Emission eines weiteren Photons der Frequenz
zur Emission eines weiteren Photons der Frequenz 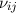 stimuliert
wird.
stimuliert
wird.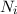 und
und 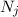 in den Zuständen
in den Zuständen 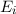 und
und 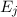 . Die
Änderung
. Die
Änderung 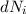 pro Zeitintervall
pro Zeitintervall  der Anzahl Atome im Zustand
der Anzahl Atome im Zustand 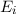 ergibt sich
aus der Differenz zwischen der Anzahl Atome
ergibt sich
aus der Differenz zwischen der Anzahl Atome 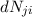 , die im Zeitintervall
, die im Zeitintervall 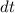 von
von
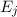 nach
nach 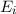 übergehen und der Anzahl Atome
übergehen und der Anzahl Atome 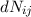 , die im Zeitintervall
, die im Zeitintervall 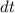 von
von
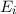 nach
nach 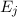 übergehen
übergehen

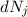 pro Zeitintervall
pro Zeitintervall 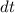 der Anzahl Atome im
Zustand
der Anzahl Atome im
Zustand 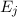 aus der Differenz zwischen der Anzahl Atome
aus der Differenz zwischen der Anzahl Atome 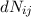 , die im
Zeitintervall
, die im
Zeitintervall 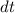 von
von  nach
nach 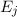 übergehen und der Anzahl Atome
übergehen und der Anzahl Atome  , die im
Zeitintervall
, die im
Zeitintervall 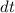 von
von 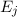 nach
nach 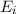 übergehen
übergehen

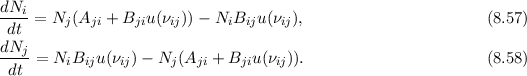
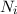 und
und 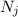 in den
Zuständen
in den
Zuständen 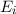 und
und  gegen einen konstanten Wert (siehe Abb.
gegen einen konstanten Wert (siehe Abb.  und
und  verschwinden.
verschwinden. 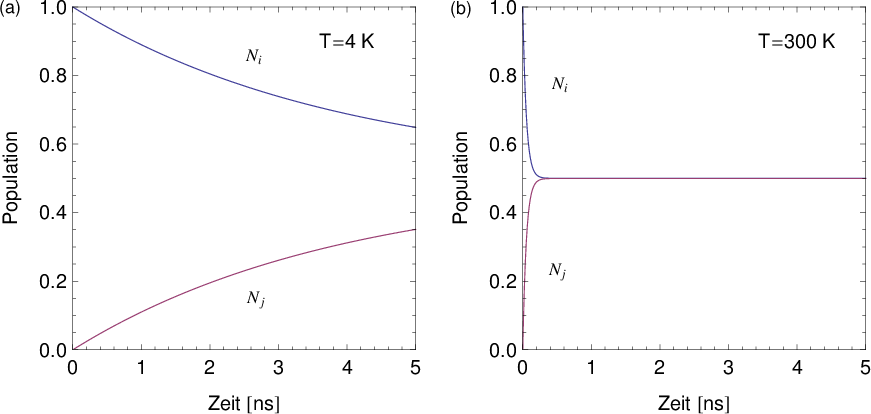
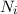 und
und 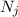 in den Zuständen
in den Zuständen 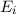 und
und 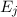 als Funktion der Zeit für die Temperaturen (a)
als Funktion der Zeit für die Temperaturen (a) 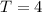 K und (b)
K und (b) 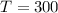 K.
Als Anfangszustände haben wir jeweils
K.
Als Anfangszustände haben wir jeweils 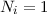 und
und 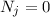 gewählt.
gewählt.
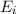 nach
nach 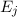 im Zeitintervall
im Zeitintervall 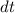 identisch
mit den Anzahl Übergängen im Zeitintervall
identisch
mit den Anzahl Übergängen im Zeitintervall 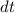 von
von 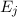 nach
nach 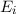 ist, d.h. es
gilt
ist, d.h. es
gilt

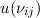 der folgende
Ausdruck
der folgende
Ausdruck

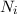 und
und 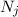 in den Zuständen
in den Zuständen 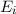 und
und
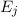 im thermischen Gleichgewicht durch die klassische Maxwell-Boltzmann-Verteilung
gegeben ist
im thermischen Gleichgewicht durch die klassische Maxwell-Boltzmann-Verteilung
gegeben ist

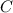 eine Konstante ist. Damit folgt für das Verhältnis der Zahl der Atome
eine Konstante ist. Damit folgt für das Verhältnis der Zahl der Atome 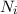 im Zustand
im Zustand 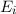 zur Zahl der Atome
zur Zahl der Atome 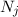 im Zustand
im Zustand 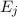


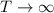 muss gelten
muss gelten 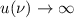 . Daraus folgt, dass die beiden B-Koeffizien-ten
identisch sein müssen
. Daraus folgt, dass die beiden B-Koeffizien-ten
identisch sein müssen

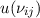

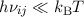 gilt das Rayleigh-Jeans-Gesetz
gilt das Rayleigh-Jeans-Gesetz

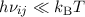 ) dann erhalten
wir
) dann erhalten
wir



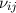 .
.
 jeder Spektrallinie eines Atoms als Differenz zwischen zwei sogenannten
Spektraltermen
jeder Spektrallinie eines Atoms als Differenz zwischen zwei sogenannten
Spektraltermen 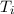 und
und 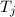 darstellen lässt und dass jede Atomsorte
einen für sie charakteristischen Satz von Spektraltermen
darstellen lässt und dass jede Atomsorte
einen für sie charakteristischen Satz von Spektraltermen 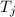 besitzt.
besitzt.

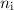 und
und 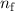 , die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und
, die sogenannten Hauptquantenzahlen, den
Anfangszustand bzw. den Endzustand bezeichnen und 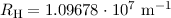 die Rydberg-Konstante ist.
die Rydberg-Konstante ist.

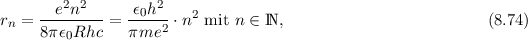
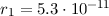 m Bohrscher Radius
genannt wird und üblicherweise mit
m Bohrscher Radius
genannt wird und üblicherweise mit 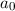 bezeichnet wird.
bezeichnet wird.

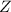 bewegt, erweitern. Berücksichtigt man zudem noch die
Bewegung des Kerns, so ergibt sich zur Beschreibung der Spektren von
wasserstoffähnlichen Systemen folgende allgemeine Formel
bewegt, erweitern. Berücksichtigt man zudem noch die
Bewegung des Kerns, so ergibt sich zur Beschreibung der Spektren von
wasserstoffähnlichen Systemen folgende allgemeine Formel
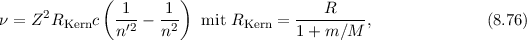
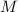 die Kernmasse bezeichnet.
die Kernmasse bezeichnet.
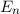 der Elektronen
der Elektronen
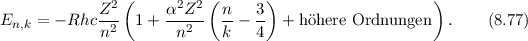
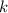 eine zweite Quantenzahl und
eine zweite Quantenzahl und 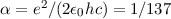 die
die
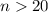 befindet und die ein wichtiger Bestandteil der Grundlagenforschung
sind.
befindet und die ein wichtiger Bestandteil der Grundlagenforschung
sind.
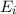 und
und 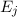 eines Atoms, so gibt es nach
Einstein die drei physikalischen Prozesse Absorption, spontane und stimulierte
Emission, die für einen Übergang zwischen diesen Niveaus verantwortlich sind.
Diese Prozesse werden durch sogenannte Einstein-Koeffizienten beschrieben. Im
thermischen Gleichgewicht erlauben sie eine alternative Herleitung des
Planckschen Strahlungsgesetzes.
eines Atoms, so gibt es nach
Einstein die drei physikalischen Prozesse Absorption, spontane und stimulierte
Emission, die für einen Übergang zwischen diesen Niveaus verantwortlich sind.
Diese Prozesse werden durch sogenannte Einstein-Koeffizienten beschrieben. Im
thermischen Gleichgewicht erlauben sie eine alternative Herleitung des
Planckschen Strahlungsgesetzes.