 )
des Wasserstoffatoms oder die Aufspaltung der Natrium-D-Linie in zwei
Linien.
)
des Wasserstoffatoms oder die Aufspaltung der Natrium-D-Linie in zwei
Linien.
Wie in Kapitel 13 angedeutet, befassen wir uns in diesem Kapitel mit der
Wechselwirkung zwischen dem Elektronspin und dem Bahndrehimpuls des Elektrons.
Diese Wechselwirkung wird Spin-Bahn-Kopplung genannt und liefert die
Erklärung der im Experiment beobachteten Feinstruktur. D.h. sie erklärt
z.B. die Aufspaltung der ersten Linie der Balmer-Serie ( )
des Wasserstoffatoms oder die Aufspaltung der Natrium-D-Linie in zwei
Linien.
)
des Wasserstoffatoms oder die Aufspaltung der Natrium-D-Linie in zwei
Linien.
Wir beginnen mit einer klassischen Beschreibung und geben eine Abschätz-ung der Grössenordnung der Spin-Bahn-Kopplung an. Anschliessend erfolgt ein kurzer Abriss der quantenmechanischen Behandlung und zum Abschluss des Kapitels befassen wir uns mit dem Einfluss eines externen Magnetfelds auf das Energiediagramm eines Atoms unter Einbezug des Elektronspins, d.h. dem sogenannten anomalen Zeeman-Effekt.
Wir zeigen in einem semiklassischen Modell wie man die Aufspaltung der
Energieniveaus mit Bahndrehimpulsquantenzahl 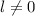 bei Einelektronenatomen und
damit insbesondere beim Wasserstoffatom, mit der Hilfe der Hypothese des
Elektronspins erklären kann. Dazu betrachten wir eine Momentaufnahme eines
Atoms mit einem Elektron, das den Kern der Ladung
bei Einelektronenatomen und
damit insbesondere beim Wasserstoffatom, mit der Hilfe der Hypothese des
Elektronspins erklären kann. Dazu betrachten wir eine Momentaufnahme eines
Atoms mit einem Elektron, das den Kern der Ladung 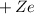 umkreist einerseits aus
der Sicht eines Beobachters im Ruhesystem des Kerns (siehe Abb. 14.1(a)) und
andererseits aus der Sicht eines Beobachters im Ruhesystem des Elektrons (siehe
Abb. 14.1(b)). In diesem rotierenden Bezugssystem des Elektrons erzeugt die
Bahnbewegung des positiv geladenen Kerns ein Magnetfeld
umkreist einerseits aus
der Sicht eines Beobachters im Ruhesystem des Kerns (siehe Abb. 14.1(a)) und
andererseits aus der Sicht eines Beobachters im Ruhesystem des Elektrons (siehe
Abb. 14.1(b)). In diesem rotierenden Bezugssystem des Elektrons erzeugt die
Bahnbewegung des positiv geladenen Kerns ein Magnetfeld 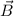 . Dieses wechselwirkt
mit dem magnetischen Moment
. Dieses wechselwirkt
mit dem magnetischen Moment 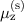 des Elektronspins und daher erhält das
Elektron die zusätzliche potentielle Energie
des Elektronspins und daher erhält das
Elektron die zusätzliche potentielle Energie 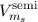 , welche nach Abschnitt 13.2
gegeben ist durch
, welche nach Abschnitt 13.2
gegeben ist durch
D.h. jeder elektronische Zustand in einem Einelektronensystem mit nichtverschwindendem Bahndrehimpuls spaltet aufgrund der Spin-Bahn-Kopplung in zwei Zustände mit unterschiedlicher Energie auf. Auf die Begründung und die Bestimmung des Magnetfelds, welches ein Beobachter im Ruhesystem des Elektrons wahrnimmt und die daraus resultierende Aufspaltung der Energieniveaus gehen wir nun etwas genauer ein.
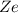 : Aus der Sicht eines Beobachters (a), (c) im
Ruhesystem des Kern und (b), (d) im Ruhesystem des Elektrons.
: Aus der Sicht eines Beobachters (a), (c) im
Ruhesystem des Kern und (b), (d) im Ruhesystem des Elektrons.Im Ruhesystem xyz des Kerns (siehe Abb. 14.1(c)) befinde sich das Elektron im
betrachteten Augenblick im Ursprung. Einfachheitshalber nehmen wir an, dass die
Geschwindigkeit des Elektrons in diesem Moment entlang der x-Achse gerichtet sei.
Ein in diesem System xyz ruhender Beobachter sagt dann, dass der Kern ein
elektrisches Feld erzeugt, das im Ursprung parallel zur y-Achse gerichtet ist und den
Betrag 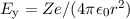 hat, wobei
hat, wobei  der Abstand zwischen Kern und Elektron
ist. In dieser Betrachtung vernachlässigen wir das (kleine) magnetische Moment des
Kerns und deshalb nimmt der Beobachter im Ruhesystem des Kerns kein Magnetfeld
wahr.
der Abstand zwischen Kern und Elektron
ist. In dieser Betrachtung vernachlässigen wir das (kleine) magnetische Moment des
Kerns und deshalb nimmt der Beobachter im Ruhesystem des Kerns kein Magnetfeld
wahr.
Wir wechseln nun zu einem Beobachter im Ruhesystem x y
y z
z des Elektrons
(siehe Abb. 14.1(d)) und fragen uns, welche elektromagnetischen Felder
dieser wahrnimmt. Die Anwendung der Transformationsformeln der speziellen
Relativitätstheorie ergeben für die Komponenten des Magnetfelds
des Elektrons
(siehe Abb. 14.1(d)) und fragen uns, welche elektromagnetischen Felder
dieser wahrnimmt. Die Anwendung der Transformationsformeln der speziellen
Relativitätstheorie ergeben für die Komponenten des Magnetfelds 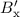 ,
, 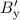 und
und 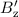 , welches der Beobachter im Ruhesystem x
, welches der Beobachter im Ruhesystem x y
y z
z des Elektrons
feststellt
des Elektrons
feststellt
wobei 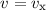 und wir im letzten Schritt die Näherung
und wir im letzten Schritt die Näherung  getroffen haben.
Der Beobachter im Ruhesystem x
getroffen haben.
Der Beobachter im Ruhesystem x y
y z
z des Elektrons stellt also ein Feld
des Elektrons stellt also ein Feld 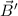 fest,
das senkrecht steht auf
fest,
das senkrecht steht auf 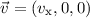 und
und 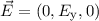 . Allgemein können wir
dies durch ein Vektorprodukt ausdrücken. Es gilt
. Allgemein können wir
dies durch ein Vektorprodukt ausdrücken. Es gilt
wobei wir die Geschwindigkeit 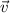 durch den Impuls
durch den Impuls 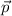 ausgedrückt haben. Das
elektrische Feld
ausgedrückt haben. Das
elektrische Feld 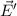 im System x
im System x y
y z
z ist in der Näherung
ist in der Näherung 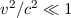 identisch
mit dem elektrischen Feld
identisch
mit dem elektrischen Feld 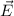 im System xyz, denn es gilt
im System xyz, denn es gilt
Das Magnetfeld 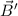 , welches das Elektron aufgrund seiner Relativbewegung zum
Kern wahrnimmt, hat zur Folge, dass das Elektron in den beiden Spinzuständen, die
durch die Quantenzahl
, welches das Elektron aufgrund seiner Relativbewegung zum
Kern wahrnimmt, hat zur Folge, dass das Elektron in den beiden Spinzuständen, die
durch die Quantenzahl 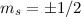 charakterisiert sind, verschiedene Energie hat.
Die Aufspaltung
charakterisiert sind, verschiedene Energie hat.
Die Aufspaltung 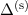 ist nach (13.17) gegeben durch
ist nach (13.17) gegeben durch
Mit (14.5), 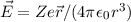 und
und 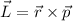 erhalten wir
erhalten wir
Dieser Ausdruck ist nicht ganz korrekt, da wir angenommen haben, dass sich das
Elektron geradlinig bewege. Da das Elektron aufgrund des Spins einen kleinen Kreisel
darstellt, spielt es eine Rolle, ob es geradeaus läuft oder den Atomkern umkreist, wie
von Llewellyn Thomas um 1926 gezeigt wurde. Die Berücksichtigung dieser
sogenannten Thomas-Präzession reduziert die Aufspaltung 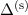 um einen Faktor
zwei1. Demzufolge lautet
die korrekte Formel2
um einen Faktor
zwei1. Demzufolge lautet
die korrekte Formel2
Die Energiedifferenz 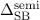 wird Spin-Bahn-Aufspaltung genannt, weshalb
wir den Index SB hinzugefügt haben. Den oberen Index s haben wir durch
den oberen Index semi ersetzt, der andeuten soll, dass unsere Herleitung
semiklassisch erfolgte. Diese Spin-Bahn-Aufspaltung erklärt insbesondere die
Aufspaltung der Spektrallinien beim Wasserstoffatom und die Aufspaltung der
Natrium-D-Linie.
wird Spin-Bahn-Aufspaltung genannt, weshalb
wir den Index SB hinzugefügt haben. Den oberen Index s haben wir durch
den oberen Index semi ersetzt, der andeuten soll, dass unsere Herleitung
semiklassisch erfolgte. Diese Spin-Bahn-Aufspaltung erklärt insbesondere die
Aufspaltung der Spektrallinien beim Wasserstoffatom und die Aufspaltung der
Natrium-D-Linie.
Ausgehend von der Formel (14.5) für die Spin-Bahn-Aufspaltung 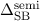 schätzen
wir die Grössenordnung der Spin-Bahn-Kopplung auf der Grundlage des Bohrschen
Atommodells (siehe Kapitel 8) für ein Einelektronenatom ab. D.h. wir nehmen an,
dass das Elektron den Kern (Ladung
schätzen
wir die Grössenordnung der Spin-Bahn-Kopplung auf der Grundlage des Bohrschen
Atommodells (siehe Kapitel 8) für ein Einelektronenatom ab. D.h. wir nehmen an,
dass das Elektron den Kern (Ladung 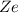 ) auf einer Kreisbahn mit Radius
) auf einer Kreisbahn mit Radius
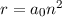 (8.27) umkreist und einen Bahndrehimpuls
(8.27) umkreist und einen Bahndrehimpuls 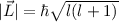 (11.47)
besitzt. Damit ergibt sich für die Spin-Bahn-Aufspaltung
(11.47)
besitzt. Damit ergibt sich für die Spin-Bahn-Aufspaltung 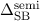 die folgende
Abschätzung
die folgende
Abschätzung
Einsetzen von 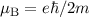 und
und 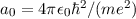 ergibt
ergibt
wobei wir verwendet haben, dass 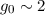 , die Feinstrukturkonstante
, die Feinstrukturkonstante 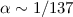 (siehe Gl. (8.50)) und die Rydberg-Energie
(siehe Gl. (8.50)) und die Rydberg-Energie 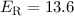 eV (siehe Abschnitt
11.2.3). Da man die Spin-Bahn-Aufspaltung Feinstruktur nennt, ergibt sich in
diesem Zusammenhang die Begründung des Namen Feinstrukturkonstante für
eV (siehe Abschnitt
11.2.3). Da man die Spin-Bahn-Aufspaltung Feinstruktur nennt, ergibt sich in
diesem Zusammenhang die Begründung des Namen Feinstrukturkonstante für
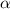 .
.
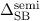 für Einelektronenatome mit
steigender Kernladungszahl
für Einelektronenatome mit
steigender Kernladungszahl 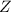 zunimmt, was im Experiment bestätigt
wird. Insbesondere wird dieser Effekt auch bei den Alkali-Atomen (siehe
Abschnitt 16.4.1) beobachtet.
zunimmt, was im Experiment bestätigt
wird. Insbesondere wird dieser Effekt auch bei den Alkali-Atomen (siehe
Abschnitt 16.4.1) beobachtet.
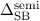 verschwindet, wenn die Bahndrehimpulsquantenzahl
verschwindet, wenn die Bahndrehimpulsquantenzahl  und somit der
Betrag des Bahndrehimpulses gleich null ist. Tatsächlich trifft dies zu, die
Spin-Bahn-Kopplung
und somit der
Betrag des Bahndrehimpulses gleich null ist. Tatsächlich trifft dies zu, die
Spin-Bahn-Kopplung 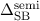 verschwindet für
verschwindet für  -Zustände. Dies kommt
auch im Erwartungswert
-Zustände. Dies kommt
auch im Erwartungswert 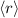 für den Bahnradius zum Ausdruck, der
für
für den Bahnradius zum Ausdruck, der
für  -Zustände verschwindet. Es sei an dieser Stelle bemerkt, dass
das Verschwinden der z-Komponente des Bahndrehimpulses (
-Zustände verschwindet. Es sei an dieser Stelle bemerkt, dass
das Verschwinden der z-Komponente des Bahndrehimpulses ( )
keine ausreichende, sondern nur eine notwendige Bedingung für das
Verschwinden der Spin-Bahn-Aufspaltung
)
keine ausreichende, sondern nur eine notwendige Bedingung für das
Verschwinden der Spin-Bahn-Aufspaltung 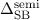 darstellt.
darstellt.
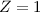 ) für den
) für den 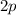 -Zustand
-Zustand 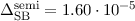 eV.
eV.
Die bisherigen Betrachtungen beruhen im Wesentlichen auf dem Bohrschen
Atommodell. Jedoch ist dieses Modell und daher auch die Ausführungen in
Abschnitt 14.1 zur Spin-Bahn-Kopplung nur begrenzt gültig (siehe Abschnitt 8.6).
Abhilfe schafft nur die rein quantenmechanische Beschreibung, auf die wir nun
in diesem Abschnitt eingehen werden. Wir beschränken uns dabei auf die
Behandlung des Wasserstoffatoms (Einelektronenatom mit Kernladungszahl
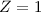 ).
).
Zur Bestimmung des Hamilton-Operators 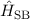 der Spin-Bahn-Kopplung des
Wasserstoffatoms stellen wir als erstes die entsprechende Hamilton-Funktion
der Spin-Bahn-Kopplung des
Wasserstoffatoms stellen wir als erstes die entsprechende Hamilton-Funktion 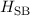 auf. Sie ist gegeben durch die Energie des magnetischen Moments (in Analogie zu
Gl. (12.8))
auf. Sie ist gegeben durch die Energie des magnetischen Moments (in Analogie zu
Gl. (12.8))
des Elektronspins 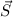 im Magnetfeld (siehe Gl. (14.5))
im Magnetfeld (siehe Gl. (14.5))
welches das Elektron in seinem Ruhesystem wahrnimmt. Damit ergibt sich mit
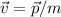 ,
, 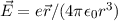 und
und 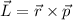 für die Hamilton-Funktion
für die Hamilton-Funktion  den
folgenden Ausdruck
den
folgenden Ausdruck
wobei 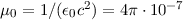 Vs/(Am) die magnetische Feldkonstante ist. Analog
zu Abschnitt 14.1 reduziert die Berücksichtigung der Thomas-Präzession diesen
Ausdruck um zwei und wir erhalten für den Hamilton-Operator
Vs/(Am) die magnetische Feldkonstante ist. Analog
zu Abschnitt 14.1 reduziert die Berücksichtigung der Thomas-Präzession diesen
Ausdruck um zwei und wir erhalten für den Hamilton-Operator 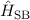 der
Spin-Bahn-Kopplung
der
Spin-Bahn-Kopplung
Damit ergibt sich für den Hamilton-Operator 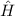 des Wasserstoffatoms unter
Berücksichtigung der Spin-Bahn-Kopplung
des Wasserstoffatoms unter
Berücksichtigung der Spin-Bahn-Kopplung
wobei wir den Hamilton-Operator ohne Spin-Bahn-Kopplung mit 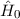 bezeichnet
haben.
bezeichnet
haben.
Ein Elektron mit Spin wird durch die Ortsvariablen  ,
, 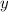 und
und  , sowie
die klassisch nicht deutbare, abstrakte Spinvariable
, sowie
die klassisch nicht deutbare, abstrakte Spinvariable 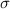 beschrieben (siehe
Kapitel 13). Diese kann nur zwei verschiedene Werte annehmen, die wir mit
„
beschrieben (siehe
Kapitel 13). Diese kann nur zwei verschiedene Werte annehmen, die wir mit
„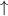 “ und „
“ und „ “ bezeichnen. Diese Eigenschaft widerspiegelt sich auch in den
Eigenwerten des Operators
“ bezeichnen. Diese Eigenschaft widerspiegelt sich auch in den
Eigenwerten des Operators 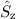 , welche gegeben sind durch
, welche gegeben sind durch 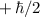 und
und
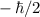 .
.
Wie zu den Ortsvariablen  ,
, 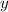 und
und  die Ortswellenfunktion
die Ortswellenfunktion 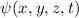 gehört,
ist der Spinvariablen
gehört,
ist der Spinvariablen 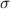 die abstrakte Spinwellenfunktion
die abstrakte Spinwellenfunktion 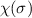 zugeordnet. Es stellt
sich nun die Frage, wie diese beiden bisher unabhängig voneinander betrachteten
Systeme (Ort und Spin) kombiniert werden können. Oder in anderen Worten: Das
Ziel ist, dass wir den Zustand eines Elektrons, welches durch die Variablen
zugeordnet. Es stellt
sich nun die Frage, wie diese beiden bisher unabhängig voneinander betrachteten
Systeme (Ort und Spin) kombiniert werden können. Oder in anderen Worten: Das
Ziel ist, dass wir den Zustand eines Elektrons, welches durch die Variablen  ,
, 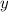 ,
,
 und
und 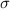 beschrieben wird, durch eine Gesamtwellenfunktion
beschrieben wird, durch eine Gesamtwellenfunktion 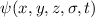 charakterisieren können, die die Spinvariable
charakterisieren können, die die Spinvariable 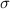 enthält und folgendermassen zu
deuten ist:
enthält und folgendermassen zu
deuten ist:
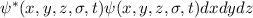 ist die Wahrscheinlichkeit, dass man ein
Elektron zur Zeit
ist die Wahrscheinlichkeit, dass man ein
Elektron zur Zeit 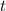 im Volumenelement
im Volumenelement 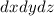 am Ort (
am Ort (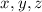 ) mit dem Wert
) mit dem Wert
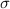 der Spinvariablen antrifft. Entsprechend ist die Wahrscheinlichkeit, dass man das
Elektron zur Zeit
der Spinvariablen antrifft. Entsprechend ist die Wahrscheinlichkeit, dass man das
Elektron zur Zeit  im besagten Volumenelement antrifft entweder mit dem Wert
„
im besagten Volumenelement antrifft entweder mit dem Wert
„ “ oder „
“ oder „ “ der Spinvariablen gegeben durch
“ der Spinvariablen gegeben durch
Dieser Ausdruck erfüllt die Normierungsbedingung, d.h. das Integral über den gesamten Ortsraum ergibt 1.
Im Zusammenhang mit der Verknüpfung der Spinvariablen 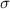 mit der
Ortswellenfunktion
mit der
Ortswellenfunktion 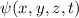 ergeben sich wie zum Teil schon angedeutet die
folgenden Fragen:
ergeben sich wie zum Teil schon angedeutet die
folgenden Fragen:
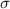 als von den Ortskoordinaten
als von den Ortskoordinaten  ,
, 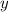 ,
,  unabhängige Variable betrachtet werden?
unabhängige Variable betrachtet werden?
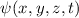 und die Spinwellenfunktion
und die Spinwellenfunktion 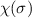 mit der Wellenfunktion
mit der Wellenfunktion 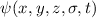 zusammen?
zusammen?
Wir werden hier auf diese Fragen eingehen. Wie in Kapitel 11 wechseln wir dazu von
den kartesischen Ortskoordinaten  ,
,  und
und  zu den Kugelkoordinaten
zu den Kugelkoordinaten  ,
, 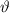 und
und 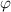 , d.h. das Elektron des Wasserstoffatoms wird durch die Ortskoordinaten
, d.h. das Elektron des Wasserstoffatoms wird durch die Ortskoordinaten  ,
,
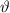 und
und 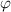 und die Spinvariable
und die Spinvariable 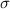 charakterisiert.
charakterisiert.
Wir vernachlässigen in einem ersten Schritt die Spin-Bahn-Kopplung und werden sie
erst in den nächsten Abschnitten wieder in unsere Betrachtungen einbinden. Damit
ist die Frage 1 beantwortet, da in diesem Fall die Spinvariable 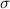 von den
Ortsvariablen
von den
Ortsvariablen  ,
, 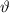 und
und 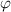 unabhängig ist. Wir kommen nun zu den Fragen 2 und
3.
unabhängig ist. Wir kommen nun zu den Fragen 2 und
3.
Wie erwähnt ist unser Ziel, die Wellenfunktion 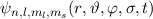 als Funktion
der Ortswellenfunktion
als Funktion
der Ortswellenfunktion 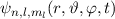 und der Spinwellenfunktion
und der Spinwellenfunktion 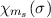 des
Wasserstoffatoms auszudrücken. Die Frage, die sich nun stellt, ist nach welchen
Kriterien wir dabei vorgehen müssen. Dabei wird sich die Tatsache, dass bei
vernachlässigter Spin-Bahn-Kopplung die beiden Spinoperatoren
des
Wasserstoffatoms auszudrücken. Die Frage, die sich nun stellt, ist nach welchen
Kriterien wir dabei vorgehen müssen. Dabei wird sich die Tatsache, dass bei
vernachlässigter Spin-Bahn-Kopplung die beiden Spinoperatoren  und
und 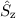 einzeln mit den Ortsoperatoren
einzeln mit den Ortsoperatoren 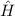 ,
, 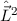 und
und 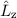 kommutieren, als entscheidend
erweisen.
kommutieren, als entscheidend
erweisen.
Zur Festlegung eines Kriteriums betrachten wir das Ort- und Spinsystem nochmals einzeln und untersuchen, durch was ein Zustand im jeweiligen System eindeutig bestimmt ist. Im Ortssystem gibt es verschiedene Möglichkeiten einen Zustand eindeutig festzulegen:
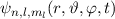 .
.
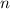 ,
, 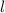 und
und 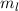 .
.
 , Quadrat des Bahndrehimpulsvektors
, Quadrat des Bahndrehimpulsvektors
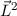 und z-Komponente des Bahndrehimpulsvektors
und z-Komponente des Bahndrehimpulsvektors  , d.h. Angabe
der Eigenwerte zur gemeinsamen Eigenfunktion
, d.h. Angabe
der Eigenwerte zur gemeinsamen Eigenfunktion 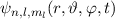 der
kommutierenden Operatoren
der
kommutierenden Operatoren 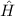 ,
, 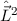 und
und 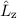 . In anderen Worten, ein
Zustand wird durch die Angabe der Eigenwerte der drei kommutierenden
Operatoren
. In anderen Worten, ein
Zustand wird durch die Angabe der Eigenwerte der drei kommutierenden
Operatoren  ,
, 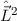 und
und 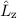 vollständig beschrieben. Man sagt dann:
Die drei Operatoren
vollständig beschrieben. Man sagt dann:
Die drei Operatoren 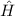 ,
, 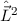 und
und 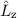 bilden einen vollständigen Satz
kommutierender Operatoren.
bilden einen vollständigen Satz
kommutierender Operatoren.Analog ergeben sich für das Spinsystem die folgenden Möglichkeiten einen Zustand eindeutig festzulegen:
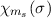 .
.
 und
und 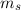 .
.
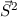 und
z-Komponente des Spinvektors
und
z-Komponente des Spinvektors  , d.h. Angabe der Eigenwerte zur
gemeinsamen Eigenfunktion
, d.h. Angabe der Eigenwerte zur
gemeinsamen Eigenfunktion 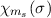 der kommutierenden Operatoren
der kommutierenden Operatoren
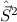 und
und 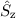 . In anderen Worten, ein Zustand wird durch die Angabe der
Eigenwerte der zwei kommutierenden Operatoren
. In anderen Worten, ein Zustand wird durch die Angabe der
Eigenwerte der zwei kommutierenden Operatoren 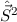 und
und 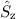 vollständig
beschrieben. Man sagt dann: Die zwei Operatoren
vollständig
beschrieben. Man sagt dann: Die zwei Operatoren 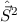 und
und 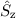 bilden
einen vollständigen Satz kommutierender Operatoren.
bilden
einen vollständigen Satz kommutierender Operatoren.Daraus wird ersichtlich, dass die den Zustand beschreibende Wellenfunktion
Eigenfunktion eines vollständigen Satzes kommutierender Operatoren ist. Wir haben
nun also ein Kriterium gefunden, mit dem wir die Gesamtwellenfunktion
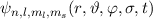 in Verbindung mit der Ortswellenfunktion
in Verbindung mit der Ortswellenfunktion 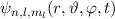 und der Spinwellenfunktion
und der Spinwellenfunktion 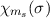 bringen können.
bringen können.
Der naheliegendste Ansatz für einen vollständigen Satz kommutierender
Operatoren für das Gesamtsystem (Ort und Spin) ist, den vollständigen Satz der
kommutierenden Operatoren des Ortssystems 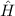 ,
, 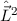 und
und 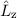 mit dem des
Spinsystems
mit dem des
Spinsystems 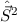 und
und 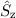 zusammenzufügen. Tatsächlich ist dies bei vernachlässigter
Spin-Bahn-Kopplung der richtige Ansatz, da in diesem Fall das Ort- und Spinsystem
zwei unabhängige Systeme darstellen und daher die Spinoperatoren
zusammenzufügen. Tatsächlich ist dies bei vernachlässigter
Spin-Bahn-Kopplung der richtige Ansatz, da in diesem Fall das Ort- und Spinsystem
zwei unabhängige Systeme darstellen und daher die Spinoperatoren 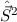 und
und 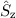 einzeln mit den Ortsoperatoren
einzeln mit den Ortsoperatoren 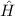 ,
, 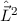 und
und 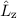 kommutieren. Folglich ist die
Gesamtwellenfunktion
kommutieren. Folglich ist die
Gesamtwellenfunktion 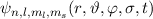 so durch die Ortswellenfunktion
so durch die Ortswellenfunktion
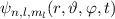 und Spinwellenfunktion
und Spinwellenfunktion 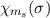 auszudrücken, dass diese
gleichzeitig Eigenfunktion der Operatoren
auszudrücken, dass diese
gleichzeitig Eigenfunktion der Operatoren 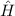 ,
, 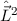 ,
, 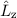 ,
, 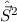 und
und 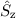 ist.
ist.
Aufgrund der Unabhängigkeit von Ort- und Spinsystem ist nun auch dieser letzte
Schritt einfach. Wir werden zeigen, dass sich sich die Gesamtwellenfunktion
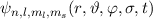 als Produkt von Ortswellenfunktion
als Produkt von Ortswellenfunktion 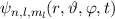 und
Spinwellenfunktion
und
Spinwellenfunktion 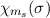 schreiben lässt, d.h. dass
schreiben lässt, d.h. dass
Wir überprüfen die Richtigkeit dieser Darstellung, indem wir die Operatoren 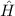 ,
, 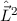 ,
,
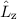 ,
, 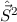 und
und 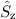 auf die durch (14.20) definierte Funktion
auf die durch (14.20) definierte Funktion 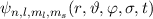 anwenden:
anwenden:
Aufgrund der vernachlässigten Spin-Bahn-Kopplung ist der Hamilton-Operator
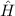 nach (11.6) gegeben durch
nach (11.6) gegeben durch
und hängt folglich nicht von der Spinvariable 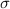 , sondern nur von den
Ortsvariablen
, sondern nur von den
Ortsvariablen  ,
, 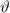 und
und 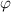 ab. Daher wirkt
ab. Daher wirkt 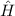 nur auf den ortsabhängigen
Teil
nur auf den ortsabhängigen
Teil 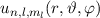 der Wellenfunktion
der Wellenfunktion 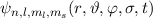 , d.h. wir
erhalten mit (11.85)
, d.h. wir
erhalten mit (11.85)
Analog erhalten wir mit (11.93)
Analog erhalten wir mit (11.94)
Analog erhalten wir mit (13.11)
Analog erhalten wir mit (13.10)
Somit ist die Richtigkeit der Darstellung (14.20) der Gesamtwellenfunktion
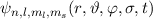 gezeigt: Die Gesamtwellenfunktion
gezeigt: Die Gesamtwellenfunktion 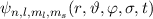 ist
das Produkt aus Ortswellenfunktion
ist
das Produkt aus Ortswellenfunktion 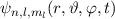 und Spinwellenfunktion
und Spinwellenfunktion
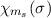 . Dies ist die Antwort auf die Frage 2. Diese Begründung der
Gesamtwellenfunktion zeigt zudem, dass Erwartungswerte, Eigenwerte und
Eigenfunktionen von Operatoren für das Gesamtsystem Ort und Spin sich aufgrund
der Tatsache berechnen lassen, dass Spinoperatoren nur auf die Spinwellenfunktion
. Dies ist die Antwort auf die Frage 2. Diese Begründung der
Gesamtwellenfunktion zeigt zudem, dass Erwartungswerte, Eigenwerte und
Eigenfunktionen von Operatoren für das Gesamtsystem Ort und Spin sich aufgrund
der Tatsache berechnen lassen, dass Spinoperatoren nur auf die Spinwellenfunktion
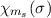 wirken und die Ortsoperatoren nur auf die Ortswellenfunktion
wirken und die Ortsoperatoren nur auf die Ortswellenfunktion
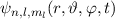 .
.
Es wird sich im Hinblick auf die quantenmechanische Behandlung der
Spin-Bahn-Kopplung (siehe Abschnitt 14.2.4) und die Betrachtung von
Mehrelektronenatomen (siehe Kapitel 16) als hilfreich erweisen, den Gesamtdrehimpuls
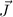 einzuführen:
einzuführen:
Definition 14.1 Der Gesamtdrehimpuls 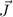 eines Einelektronensystems ist
definiert als Summe von Bahndrehimpuls
eines Einelektronensystems ist
definiert als Summe von Bahndrehimpuls 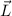 und Spin
und Spin 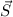
Der entsprechende Gesamtdrehimpulsoperator 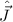 ergibt sich analog zu
ergibt sich analog zu
Die im letzten Abschnitt 14.2.2 kennengelernten Produktwellenfunktionen
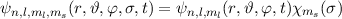 sind zwar auch Eigenfunktionen der
z-Komponente des Gesamtdrehimpulsoperators
sind zwar auch Eigenfunktionen der
z-Komponente des Gesamtdrehimpulsoperators 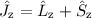 zum Eigenwert
zum Eigenwert
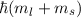 , jedoch nicht vom Quadrat des Gesamtdrehimpulsoperators
, jedoch nicht vom Quadrat des Gesamtdrehimpulsoperators  ,
da
,
da
Jedoch ist es für die zu Beginn erwähnten Fragestellungen von Vorteil mit Zuständen
zu rechnen, die auch Eigenfunktion von 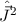 sind. Wir wechseln daher vom bisherigen
vollständigen Satz kommutierender Operatoren
sind. Wir wechseln daher vom bisherigen
vollständigen Satz kommutierender Operatoren 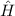 ,
, 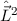 ,
,  ,
, 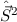 und
und 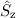 zum
neuen ebenfalls vollständigen Satz kommutierender Operatoren
zum
neuen ebenfalls vollständigen Satz kommutierender Operatoren 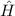 ,
, 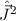 ,
, 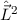 ,
, 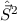 und
und 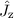 und suchen die entsprechenden Eigenfunktionen
und suchen die entsprechenden Eigenfunktionen 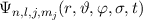 mit
den Eigenwerten
mit
den Eigenwerten 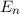 ,
, 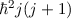 ,
, 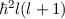 ,
, 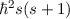 und
und 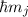 . D.h. unsere
Aufgaben sind:
. D.h. unsere
Aufgaben sind:
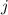 annehmen kann.
Dadurch sind dann auch die Werte von
annehmen kann.
Dadurch sind dann auch die Werte von 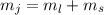 bestimmt
bestimmt
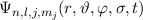 durch die
Produktwellenfunktionen
durch die
Produktwellenfunktionen  .
.Wir verzichten hier auf eine ausführliche Herleitung und geben direkt die Lösung für das Wasserstoffatom an3:
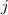 kann die Werte
kann die Werte 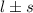 annehmen, d.h.
annehmen, d.h. 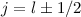 ,
wobei
,
wobei 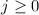 .
.
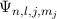 sind gegeben durch
sind gegeben durch dabei haben wir für eine bessere Übersichtlichkeit auf das Aufführen der
unabhängigen Variablen  ,
, 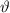 ,
, 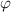 ,
, 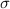 und
und 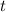 verzichtet.
verzichtet.
Wir betrachten als Beispiel den 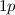 -Zustand, d.h.
-Zustand, d.h. 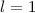 und
und 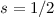 . Die
Quantenzahl
. Die
Quantenzahl 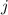 kann dann die beiden Werte
kann dann die beiden Werte 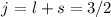 und
und 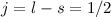 annehmen. Die entsprechenden Eigenfunktionen
annehmen. Die entsprechenden Eigenfunktionen 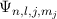 sind in Tab. 14.1
dargestellt und Abb. 14.2 zeigt die graphische Darstellung der entsprechenden
Gesamtdrehimpulsvektoren im Bezug zur z-Achse.
sind in Tab. 14.1
dargestellt und Abb. 14.2 zeigt die graphische Darstellung der entsprechenden
Gesamtdrehimpulsvektoren im Bezug zur z-Achse.
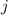 | 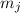 | 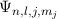 |
| 3/2 | -3/2 | 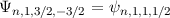 |
| -1/2 | 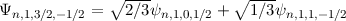 |
|
| 1/2 | 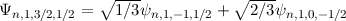 |
|
| 3/2 | 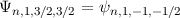 |
|
| 1/2 | -1/2 | 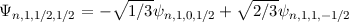 |
| 1/2 | 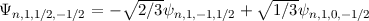 |
|
 des vollständigen Satzes von
kommutierenden Operatoren
des vollständigen Satzes von
kommutierenden Operatoren  ,
, 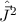 ,
, 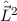 ,
, 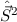 und
und 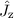 zu den
entsprechenden Quantenzahlen
zu den
entsprechenden Quantenzahlen 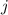 und
und 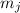 für den
für den 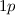 -Zustand.
-Zustand.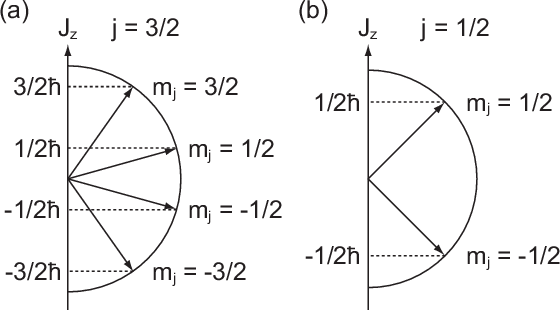
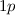 -Zustand: Für die Quantenzahlen (a)
-Zustand: Für die Quantenzahlen (a) 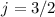 und (b)
und (b) 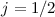 sind jeweils
die möglichen Gesamtdrehimpulsvektoren im Bezug zur z-Achse eingezeichnet.
sind jeweils
die möglichen Gesamtdrehimpulsvektoren im Bezug zur z-Achse eingezeichnet.Bevor wir auf die rein quantenmechanische Behandlung eingehen werden, befassen wir uns mit einem weiteren semiklassischen Modell der Spin-Bahn-Kopplung.
Als erstes drücken wir den Hamilton-Operator 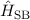 , welcher die Spin-Bahn-Kopplung
beschreibt, durch den Gesamtdrehimpulsoperator
, welcher die Spin-Bahn-Kopplung
beschreibt, durch den Gesamtdrehimpulsoperator 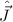 aus und zeigen, dass die
Wellenfunktionen
aus und zeigen, dass die
Wellenfunktionen  Eigenfunktionen von
Eigenfunktionen von 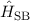 sind. Da die Operatoren
sind. Da die Operatoren 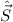 und
und 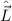 kommutieren, gilt
kommutieren, gilt
und damit
Einsetzen in (14.17) liefert
und damit
Damit sind die Eigenfunktionen 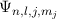 Eigenfunktionen des Hamilton-Opera-tors
Eigenfunktionen des Hamilton-Opera-tors
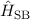 mit den Eigenwerten
mit den Eigenwerten
wobei die Spin-Bahn-Kopplungskonstante 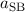 gegeben ist durch
gegeben ist durch
Indem wir den klassischen Bahnradius  stehengelassen und in die
Spin-Bahn-Kopplungskonstante
stehengelassen und in die
Spin-Bahn-Kopplungskonstante 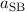 integriert haben, sind wir an dieser Stelle von
der rein quantenmechanischen Behandlung abgekommen und zu einer semiklassischen
Betrachtung übergegangen.
integriert haben, sind wir an dieser Stelle von
der rein quantenmechanischen Behandlung abgekommen und zu einer semiklassischen
Betrachtung übergegangen.
Die Wellenfunktionen 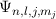 sind Eigenfunktionen des Hamilton-Opera-tors
sind Eigenfunktionen des Hamilton-Opera-tors
 zum Eigenwert
zum Eigenwert 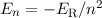 . Mit (14.37) ergibt sich somit für die
Eigenwerte des Gesamt-Hamilton-Operators
. Mit (14.37) ergibt sich somit für die
Eigenwerte des Gesamt-Hamilton-Operators 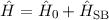 und damit für
die Energiewerte
und damit für
die Energiewerte 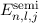 des Wasserstoffatoms unter Berücksichtigung der
Spin-Bahn-Kopplung
des Wasserstoffatoms unter Berücksichtigung der
Spin-Bahn-Kopplung
wobei wir für die Energiewerte neu die Indizes 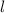 und
und 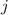 eingeführt haben. Wir
werden als nächstes diese semiklassische Betrachtung fortsetzen und die daraus
abgeleiteten Konsequenzen für das Energiediagramm des Wasserstoffatoms
betrachten.
eingeführt haben. Wir
werden als nächstes diese semiklassische Betrachtung fortsetzen und die daraus
abgeleiteten Konsequenzen für das Energiediagramm des Wasserstoffatoms
betrachten.
Die Energiewerte 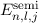 des Wasserstoffatom hängen neu zusätzlich von den
Quantenzahlen
des Wasserstoffatom hängen neu zusätzlich von den
Quantenzahlen 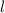 und
und 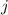 ab. Für feste Quantenzahlen
ab. Für feste Quantenzahlen 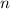 und
und 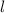 ergibt sich mit
Ausnahme für die
ergibt sich mit
Ausnahme für die  -Zustände (
-Zustände (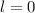 ) damit eine Aufspaltung in zwei Energiewerte
) damit eine Aufspaltung in zwei Energiewerte
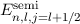 und
und 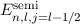 . Die Energiedifferenz
. Die Energiedifferenz 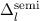 dieser beiden Zustände
ist gegeben durch
dieser beiden Zustände
ist gegeben durch
Wir führen nun eine neue in der Literatur übliche Symbolik für die Benennung der Zustände ein:
Ein Zustand mit Hauptquantenzahl 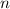 , Bahndrehimpulsquantenzahl
, Bahndrehimpulsquantenzahl 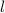 ,
Spinquantenzahl
,
Spinquantenzahl  und Gesamtdrehimpulsquantenzahl
und Gesamtdrehimpulsquantenzahl 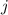 erhält folgende
Bezeichnung
erhält folgende
Bezeichnung
wobei für 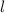 jeweils der entsprechende Buchstabe
jeweils der entsprechende Buchstabe 
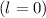 ,
, 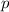
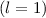 , ...
einzusetzen ist.
, ...
einzusetzen ist.
In Tab. 14.2 sind die Zustände 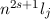 und die entsprechenden Energiewerte
und die entsprechenden Energiewerte
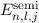 des Wasserstoffatoms (
des Wasserstoffatoms (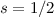 ) für die Hauptquantenzahlen
) für die Hauptquantenzahlen 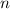 = 1, 2 und
3 zusammengestellt. Das entsprechende Energiediagramm (siehe Abb. 14.3) lässt die
Spin-Bahn-Kopplung-Aufspaltung für Zustände mit Bahndrehimpulsquantenzahl
= 1, 2 und
3 zusammengestellt. Das entsprechende Energiediagramm (siehe Abb. 14.3) lässt die
Spin-Bahn-Kopplung-Aufspaltung für Zustände mit Bahndrehimpulsquantenzahl
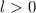 erkennen.
erkennen.
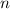 | 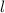 | 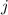 | 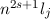 | 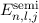 |
| 1 | 0 | 1/2 | 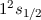 | 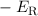 |
| 2 | 0 | 1/2 | 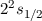 | 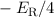 |
| 1 | 1/2 | 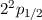 | 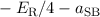 |
|
| 3/2 | 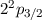 | 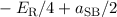 |
||
| 3 | 0 | 1/2 | 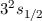 | 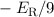 |
| 1 | 1/2 | 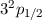 | 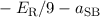 |
|
| 3/2 | 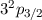 | 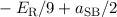 |
||
| 2 | 3/2 | 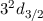 | 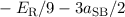 |
|
| 5/2 | 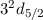 | 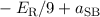 |
||
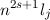 und die entsprechenden Energiewerten
und die entsprechenden Energiewerten
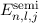 des Wasserstoffatoms unter Berücksichtigung der Spin-Bahn-Kopplung
für die Hauptquantenzahlen
des Wasserstoffatoms unter Berücksichtigung der Spin-Bahn-Kopplung
für die Hauptquantenzahlen  = 1, 2 und 3.
= 1, 2 und 3.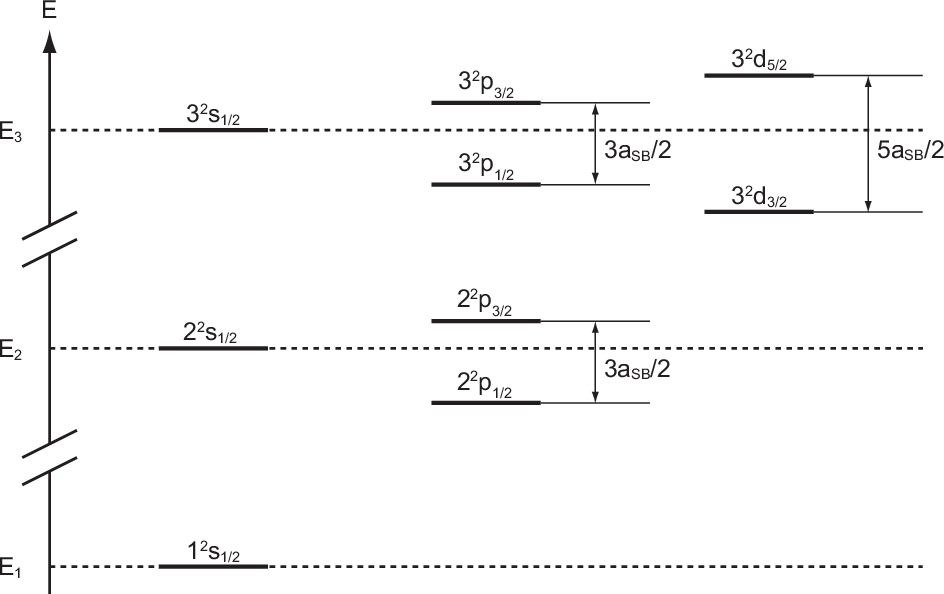
 = 1, 2 und
3. Die gestrichelten Linien geben die Energieterme
= 1, 2 und
3. Die gestrichelten Linien geben die Energieterme 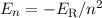 bei
vernachlässigter Spin-Bahn-Kopplung an.
bei
vernachlässigter Spin-Bahn-Kopplung an.Da wir die wesentlichen Merkmale der Spin-Bahn-Kopplung und deren Auswirkungen auf das Energiediagramm des Wasserstoffatoms bereits mit unserem semiklassischen Modell beschreiben konnten, werden wir nur einen kurzen Überblick über die wesentlichen Schritte und Resultate der quantenmechanischen Berechnung geben und für genauere Ausführungen auf weiterführende Literatur [11] verweisen.
Die rein quantenmechanische Behandlung erfolgt innerhalb der
Rayleigh-Schrödinger-Störungstheorie indem man vom Hamilton-Operator 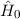 ausgeht
und den Hamilton-Operator
ausgeht
und den Hamilton-Operator 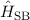 der Spin-Bahn-Kopplung als Störung einführt. Die
Energieverschiebung
der Spin-Bahn-Kopplung als Störung einführt. Die
Energieverschiebung 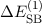 in 1. Ordnung ist dabei durch den Erwartungswert
in 1. Ordnung ist dabei durch den Erwartungswert 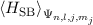 gegeben4.
Mit (14.17) und
gegeben4.
Mit (14.17) und  erhalten wir
erhalten wir
Wir verzichten auf die Berechnung des Erwartungswerts 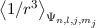 und geben
hier nur das Resultat wider. Es ergibt sich
und geben
hier nur das Resultat wider. Es ergibt sich
Einsetzen in (14.42) liefert
Es sei bemerkt, dass dieser Ausdruck für 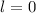 divergiert und daher nur
für
divergiert und daher nur
für 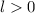 gilt. Für
gilt. Für 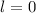 verschwindet
verschwindet 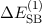 . Damit ergeben sich unter
Berücksichtigung der Spin-Bahn-Kopplung die folgenden Energiewerte
. Damit ergeben sich unter
Berücksichtigung der Spin-Bahn-Kopplung die folgenden Energiewerte 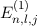 für das
Wasserstoffatom
für das
Wasserstoffatom
Wir haben bisher davon gesprochen, dass die Spin-Bahn-Kopplung für die
Fein-struktur verantwortlich ist. Um genau zu sein, ist dies nicht ganz korrekt, da
neben der Energiekorrektur 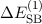 , bewirkt durch die Spin-Bahn-Kopplung, noch
zwei weitere Korrekturterme existieren. Alle drei Korrekturen werden unter
dem Namen relativistische Korrekturen zusammengefasst und bewirken die
Feinstrukturaufspaltung. Wir geben als nächstes eine kurze Auflistung der beiden
zusätzlichen Korrekturterme an und gehen dann auf die Gesamtlösung für die
relativistisch korrigierten Energiewerte des Wasserstoffatoms ein.
, bewirkt durch die Spin-Bahn-Kopplung, noch
zwei weitere Korrekturterme existieren. Alle drei Korrekturen werden unter
dem Namen relativistische Korrekturen zusammengefasst und bewirken die
Feinstrukturaufspaltung. Wir geben als nächstes eine kurze Auflistung der beiden
zusätzlichen Korrekturterme an und gehen dann auf die Gesamtlösung für die
relativistisch korrigierten Energiewerte des Wasserstoffatoms ein.
Bisher haben wir das Elektron als nicht-relativistisches Teilchen betrachtet.
Entwickelt man jedoch den relativistischen Ausdruck für die Energie 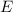 für
kleine Werte von
für
kleine Werte von 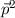 ergibt sich
ergibt sich
Terme höherer Ordnung können vernachlässigt werden, wenn 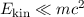 ,
d.h.
,
d.h. 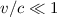 , was beim Wasserstoffatom für kleine Werte der magnetischen
Quantenzahl
, was beim Wasserstoffatom für kleine Werte der magnetischen
Quantenzahl 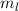 gegeben ist. Damit ergibt sich zum Hamilton-Operator
gegeben ist. Damit ergibt sich zum Hamilton-Operator 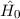 als Störung der relativistische Hamilton-Operator
als Störung der relativistische Hamilton-Operator
Die entsprechende Energiewertkorrektur 1. Ordnung ist gegeben durch
Das Elektron des Wasserstoffatoms ist nicht genau lokalisiert sondern schwankt
bzgl. seiner Position im Bereich von 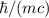 . Diese „Zitterbewegung“ wird
durch den zusätzlichen Hamilton-Operator
. Diese „Zitterbewegung“ wird
durch den zusätzlichen Hamilton-Operator 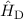 berücksichtigt, welcher
gegeben ist durch
berücksichtigt, welcher
gegeben ist durch
wobei 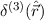 den Diracschen Deltaoperator in drei Dimensionen bezeichnet.
Damit ergibt sich in 1. Ordnung der folgende Korrekturterm
den Diracschen Deltaoperator in drei Dimensionen bezeichnet.
Damit ergibt sich in 1. Ordnung der folgende Korrekturterm
D.h. der Darwin-Term liefert nur einen Beitrag für 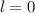 .
.
Die drei Korrekturen 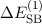 ,
, 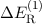 und
und 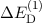 führen zusammen zu folgendem
Ausdruck für die Energiewerte
führen zusammen zu folgendem
Ausdruck für die Energiewerte 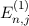 des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen
des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen
D.h. die Energiewerte 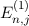 des Wasserstoffatoms hängen nur von den
Quantenzahlen
des Wasserstoffatoms hängen nur von den
Quantenzahlen 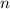 und
und 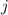 , aber nicht von der Bahndrehimpulsquantenzahl
, aber nicht von der Bahndrehimpulsquantenzahl 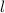 ab5.
Die Berücksichtigung aller drei relativistischen Korrekturen liefert also eine Korrektur
gegenüber dem Ausdruck (14.45) für die Energiewerte
ab5.
Die Berücksichtigung aller drei relativistischen Korrekturen liefert also eine Korrektur
gegenüber dem Ausdruck (14.45) für die Energiewerte 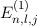 des Wasserstoffatoms
unter Berücksichtigung der Spin-Bahn-Kopplung. Die korrigierten Energiewerte
des Wasserstoffatoms
unter Berücksichtigung der Spin-Bahn-Kopplung. Die korrigierten Energiewerte 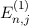 zu den Zuständen
zu den Zuständen  des Wasserstoffatoms für die Hauptquantenzahlen
des Wasserstoffatoms für die Hauptquantenzahlen 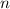 =
1, 2 und 3 sind in Tab. 14.3 zusammengestellt. Das entsprechende Energiediagramm
(siehe Abb. 14.4) gibt die Feinstrukturaufspaltung beim Wasserstoffatom wieder.
=
1, 2 und 3 sind in Tab. 14.3 zusammengestellt. Das entsprechende Energiediagramm
(siehe Abb. 14.4) gibt die Feinstrukturaufspaltung beim Wasserstoffatom wieder.
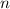 | 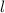 | 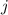 | 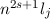 | 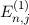 |
| 1 | 0 | 1/2 | 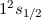 | 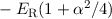 |
| 2 | 0 | 1/2 | 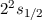 | 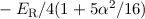 |
| 1 | 1/2 | 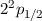 | 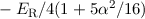 |
|
| 3/2 | 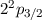 | 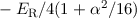 |
||
| 3 | 0 | 1/2 | 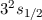 | 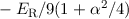 |
| 1 | 1/2 | 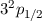 | 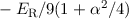 |
|
| 3/2 | 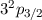 | 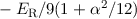 |
||
| 2 | 3/2 | 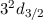 | 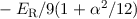 |
|
| 5/2 | 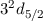 | 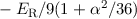 |
||
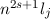 und die entsprechenden Energiewerten
und die entsprechenden Energiewerten
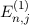 des Wasserstoffatoms unter Berücksichtigung der drei relativistischen
Korrekturen Spin-Bahn-Kopplung, Relativistische Korrektur und Darwin-Term
für die Hauptquantenzahlen
des Wasserstoffatoms unter Berücksichtigung der drei relativistischen
Korrekturen Spin-Bahn-Kopplung, Relativistische Korrektur und Darwin-Term
für die Hauptquantenzahlen  = 1, 2 und 3.
= 1, 2 und 3.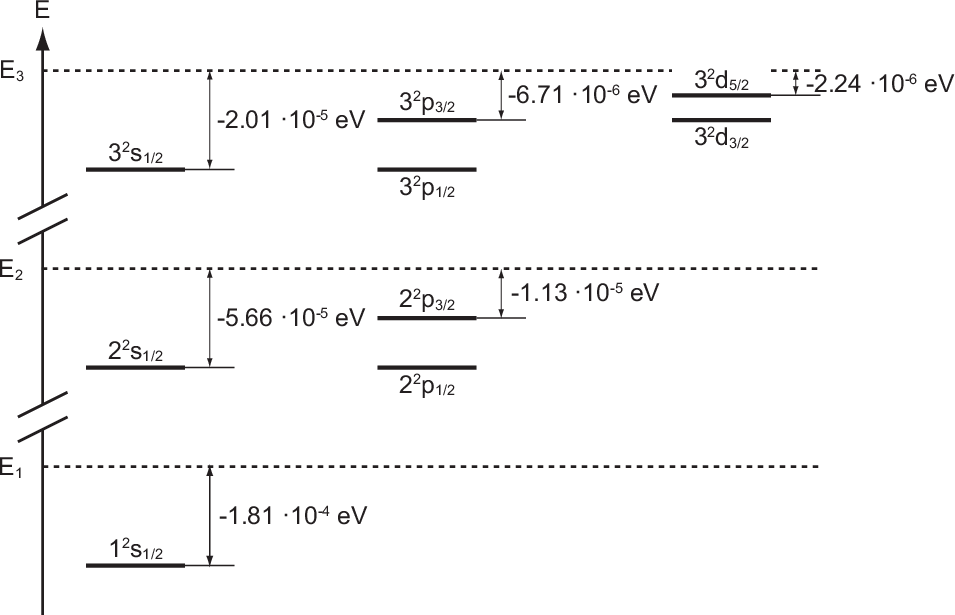
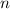 = 1, 2 und 3. Die
gestrichelten Linien geben die Energieterme
= 1, 2 und 3. Die
gestrichelten Linien geben die Energieterme 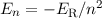 an.
an.Neben diesen relativistischen Korrekturen, welche für die Feinstrukturaufspaltung des Wasserstoffatoms verantwortlich sind, ergeben sich noch weitere Korrekturen, wenn man noch zusätzlich den Kern-Spin berücksichtigt. Diese Korrekturen bestimmen die sogenannte Hyperfeinstruktur.
In Kapitel 12 haben wir den sogenannten normalen Zeeman-Effekt besprochen,
d.h. den Effekt eines homogenen externen Magnetfelds auf die Energieniveaus und
damit das Spektrum des Wasserstoffatoms unter Vernachlässigung des Elektronspins.
Wir berücksichtigen nun den Elektronspin, d.h. wir betrachten den Effekt eines
homogenen externen Magnetfelds 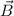 auf die Energieniveaus
auf die Energieniveaus 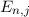 (siehe
Gl. (14.51)) des Wasserstoffatoms.
(siehe
Gl. (14.51)) des Wasserstoffatoms.
Der Gesamt-Hamilton-Operator 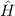 setzt sich nun aus
setzt sich nun aus 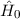 den drei relativistischen
Korrekturen
den drei relativistischen
Korrekturen 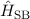 ,
, 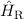 und
und 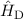 , sowie dem Zeeman-Term
, sowie dem Zeeman-Term 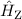 zusammen. Mit
zusammen. Mit
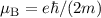 , (13.16) und (13.18) ist
, (13.16) und (13.18) ist 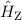 gegeben durch
gegeben durch
wobei wir angenommen haben, dass 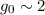 . Wir beschränken uns hier auf den Fall
kleiner Magnetfelder, d.h.
. Wir beschränken uns hier auf den Fall
kleiner Magnetfelder, d.h. 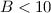 T. In diesem Fall können wir den Zeeman-Term
T. In diesem Fall können wir den Zeeman-Term
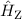 als Störung gegenüber dem Hamilton-Operator
als Störung gegenüber dem Hamilton-Operator 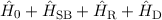 betrachten und die durch das homogene externe Magnetfeld
betrachten und die durch das homogene externe Magnetfeld 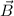 bewirkte
Energieverschiebung
bewirkte
Energieverschiebung 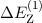 mittels Rayleigh-Schrödinger-Störungstheorie
berechnen. Dann ist
mittels Rayleigh-Schrödinger-Störungstheorie
berechnen. Dann ist 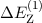 gegeben durch den Erwartungswert
gegeben durch den Erwartungswert 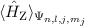 des
Zeeman-Terms6
und wir erhalten mit (14.52)
des
Zeeman-Terms6
und wir erhalten mit (14.52)
Wir verzichten hier auf die Berechnung des Erwartungswerts 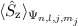 und geben
direkt das Resultat für
und geben
direkt das Resultat für 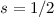 an
an
Für genaue Ausführungen verweisen wir auf weiterführende Literatur [11]. Einsetzen in (14.53) liefert
wobei der Landé-Faktor 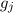 gegeben ist durch
gegeben ist durch
Wir fassen zusammen:
Für die Energiewerte 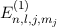 des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen im homogenen externen Magnetfeld
des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen im homogenen externen Magnetfeld 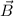 ergibt sich das
folgende Schlussresultat
ergibt sich das
folgende Schlussresultat
wobei der Landé-Faktor 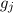 gegeben ist durch
gegeben ist durch
Abb. 14.5 zeigt die durch den anomalen Zeeman-Effekt bewirkte Aufspaltung der
Zustände 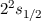 ,
, 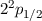 und
und 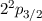 des Wasserstoffatoms.
des Wasserstoffatoms.
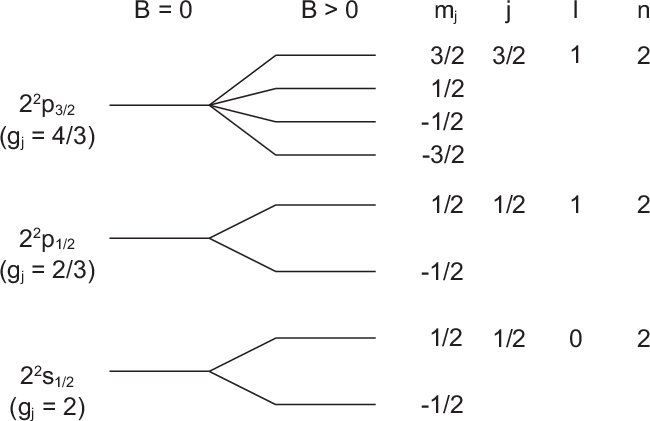
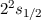 ,
, 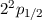 und
und 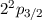 des
Wasserstoffatoms aufgrund des anomalen Zeeman-Effekts.
des
Wasserstoffatoms aufgrund des anomalen Zeeman-Effekts.
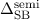 den
Ausdruck
den
Ausdruck
Das Modell zeigt damit in Übereinstimmung mit dem Experiment, dass die
Spin-Bahn-Aufspaltung mit steigender Kernladungszahl 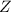 zunimmt und für
den Wert null für die Bahndrehimpulsquantenzahl
zunimmt und für
den Wert null für die Bahndrehimpulsquantenzahl 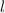 verschwindet. Zudem
liefert es die Grössenordnung für die Spin-Bahn-Aufspaltung. Für den
verschwindet. Zudem
liefert es die Grössenordnung für die Spin-Bahn-Aufspaltung. Für den
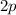 -Zustand des Wasserstoffatoms erhalten wir zum Beispiel einen Wert von
der Grössenordnung
-Zustand des Wasserstoffatoms erhalten wir zum Beispiel einen Wert von
der Grössenordnung 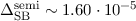 eV.
eV.
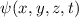 und die Spinwellenfunktion
und die Spinwellenfunktion 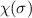 zu
einer Gesamtwellenfunktion
zu
einer Gesamtwellenfunktion 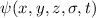 zu kombinieren. Unter
Vernachlässigung der Spin-Bahn-Kopplung können Ort- und Spinsystem
voneinander unabhängig betrachtet werden und die Gesamtwellenfunktion
zu kombinieren. Unter
Vernachlässigung der Spin-Bahn-Kopplung können Ort- und Spinsystem
voneinander unabhängig betrachtet werden und die Gesamtwellenfunktion
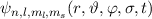 des Wasserstoffatoms lässt sich dann als Produkt von
Ortswellenfunktion
des Wasserstoffatoms lässt sich dann als Produkt von
Ortswellenfunktion 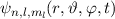 und Spinwellenfunktion
und Spinwellenfunktion 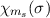 schreiben.
schreiben.
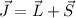 einzuführen. Die Produktwellenfunktionen
einzuführen. Die Produktwellenfunktionen
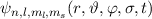 sind zwar auch Eigenfunktionen der z-Komponente
des Gesamtdrehimpulsoperators
sind zwar auch Eigenfunktionen der z-Komponente
des Gesamtdrehimpulsoperators 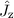 , jedoch nicht vom Quadrat des
Gesamtdrehimpulsoperators
, jedoch nicht vom Quadrat des
Gesamtdrehimpulsoperators 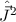 . Daher wechselt man vom bisherigen
vollständigen Satz kommutierender Operatoren
. Daher wechselt man vom bisherigen
vollständigen Satz kommutierender Operatoren  ,
, 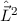 ,
, 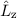 ,
, 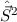 und
und 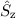 zum neuen ebenfalls vollständigen Satz kommutierender Operatoren
zum neuen ebenfalls vollständigen Satz kommutierender Operatoren 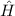 ,
, 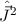 ,
,
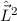 ,
, 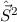 und
und 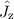 . Die entsprechenden Eigenfunktionen
. Die entsprechenden Eigenfunktionen 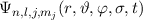 mit den Eigenwerten
mit den Eigenwerten 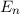 ,
, 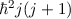 ,
, 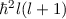 ,
, 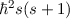 und
und
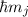 lassen sich als Linearkombination der Produktwellenfunktionen
lassen sich als Linearkombination der Produktwellenfunktionen
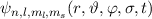 schreiben. Die neuen Quantenzahlen
schreiben. Die neuen Quantenzahlen 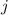 und
und 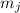 können dabei die Werte
können dabei die Werte 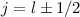 , wobei
, wobei 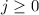 bzw.
bzw. 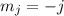 ,
, 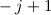 ,
...,
,
..., 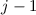 ,
, 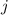 annehmen.
annehmen.
 des Wasserstoffatoms unter
Berücksichtigung der Spin-Bahn-Kopplung
des Wasserstoffatoms unter
Berücksichtigung der Spin-Bahn-Kopplung
D.h. für feste Quantenzahlen 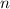 und
und 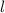 ergibt sich mit Ausnahme für die
ergibt sich mit Ausnahme für die
 -Zustände (
-Zustände (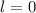 ) eine Aufspaltung in zwei Energiewerte.
) eine Aufspaltung in zwei Energiewerte.
 , Bahndrehimpulsquantenzahl
, Bahndrehimpulsquantenzahl 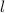 , Spinquantenzahl
, Spinquantenzahl  und
Gesamtdrehimpulsquantenzahl
und
Gesamtdrehimpulsquantenzahl 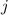 die Bezeichnung
die Bezeichnung 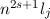 verwendet.
verwendet.
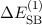 , bewirkt
durch die Spin-Bahn-Kopplung, noch zwei weitere Korrekturterme: Der
relativistische Korrekturterm und der Darwin-Term. Alle drei Korrekturen
werden unter dem Namen relativistische Korrekturen zusammengefasst und
bewirken die Feinstrukturaufspaltung. Für die Energiewerte
, bewirkt
durch die Spin-Bahn-Kopplung, noch zwei weitere Korrekturterme: Der
relativistische Korrekturterm und der Darwin-Term. Alle drei Korrekturen
werden unter dem Namen relativistische Korrekturen zusammengefasst und
bewirken die Feinstrukturaufspaltung. Für die Energiewerte 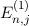 des
Wasserstoffatoms unter Berücksichtigung relativistischer Korrekturen ergibt
sich nach der Rayleigh-Schrödinger-Störungstheorie (1. Ordnung)
des
Wasserstoffatoms unter Berücksichtigung relativistischer Korrekturen ergibt
sich nach der Rayleigh-Schrödinger-Störungstheorie (1. Ordnung)
D.h. die Energiewerte 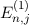 des Wasserstoffatoms hängen nur von den
Quantenzahlen
des Wasserstoffatoms hängen nur von den
Quantenzahlen 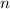 und
und 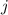 , aber nicht von der Bahndrehimpulsquantenzahl
, aber nicht von der Bahndrehimpulsquantenzahl
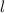 ab. Diese Aussage gilt nur für das Wasserstoffatom bzw. für
Einelektronenatome und nicht für Mehrelektronenatome. Dort haben Zustände
mit verschiedenen Werten für
ab. Diese Aussage gilt nur für das Wasserstoffatom bzw. für
Einelektronenatome und nicht für Mehrelektronenatome. Dort haben Zustände
mit verschiedenen Werten für 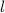 aber gleichem
aber gleichem 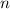 und
und 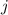 unterschiedliche
Energien.
unterschiedliche
Energien.
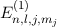 des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen im homogenen externen Magnetfeld
des Wasserstoffatoms unter Berücksichtigung
relativistischer Korrekturen im homogenen externen Magnetfeld 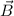 ergibt sich
nach der Rayleigh-Schrödinger-Störungstheorie (1. Ordnung)
ergibt sich
nach der Rayleigh-Schrödinger-Störungstheorie (1. Ordnung)
wobei der Landé-Faktor 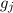 gegeben ist durch
gegeben ist durch
Das bedeutet, dass durch ein homogenes externes Magnetfeld 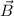 die
durch die Quantenzahl
die
durch die Quantenzahl 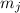 bewirkte Entartung der Energiewerte
bewirkte Entartung der Energiewerte
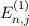 aufgehoben wird. Dieser Effekt wird anomaler Zeeman-Effekt
genannt.
aufgehoben wird. Dieser Effekt wird anomaler Zeeman-Effekt
genannt.