One important key characteristics of a non-classical physical system is entanglement. For a system containing three qubits two important classes of entangled states are GHZ- and W-states. The first class consists of superposition states between |000⟩ and |111⟩ and the second one arises when a single excitation is symmetrically shared between three qubits, i.e. in an equal superposition between |001⟩, |010⟩ and |100⟩. In our experiment [1] we have exploited the resonant interaction between three superconducting transmon-type qubits and a microwave transmission line resonator to show that a W-state can be generated with high efficiency in this system by harnessing its collective dynamics. Interestingly, our method also benefits from the √N-nonlinearity of the coupling strength between N qubits and a single field mode. Thus in contrast to many entangling gates our scheme is actually faster for a larger number of qubits and thus also is expected to be less affected by dephasing and relaxation.

To generate the W-state we first populate the resonator with a single photon by using a single qubit vacuum Rabi π-pulse. Then the two remaining qubits are also tuned into resonance. The single photon now has equal probability to be absorbed by each of the three qubits. Our lack of knowledge about which qubit the photon finally excites, naturally leads to a W-type entangled state.

We use full quantum state tomography to characterize the degree of entanglement generated (see figure 1). To better understand the limitations of our collective method we also employ a procedure, in which the excitation is distributed sequentially by tuning the qubits in and out of resonance one after another. In fact this method leads to a higher fidelity, which suggests that the main limitation in the collective approach is due to on-chip crosstalk among the flux lines, which are used for fast tuning of the qubit transition frequencies.

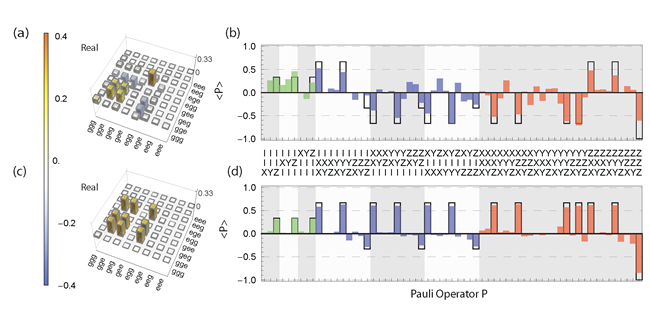
Figure 1: Real part of the density matrix of the W-state for (a) the collective approach and (c) the sequential approach. (b/d) are Pauli sets for the collective/sequential approach, respectively.

Full article:
http://pra.aps.org/abstract/PRA/v86/i5/e053838, also in arXiv:1202.5191