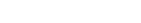When a quantum mechanical system evolves under a time-dependent Hamiltonian, it acquires not only the wellknown dynamic phase, which is the time-integral of the energy of the system, but also a geometric phase. As indicated by its name, it is of a purely geometric nature in that it solely depends on the trajectory of the quantum system in state space.
One way to measure geometric phases is to employ a superposition of ground and first excited state of a two-level system (a qubit). In previous studies [1], we have observed geometric phases in a Cooper pair box, a superconducting quantum system with large anharmonicity. In this system, the energy levels defining the qubit are well separated from higher energy levels. To explore the effects of higher energy levels, we make use of a superconducting transmontype qubit with low anharmonicity. We measure the contribution of the second excited state to the geometric phase (Fig. 1a) and find very good agreement with theory treating higher levels perturbatively [2]. Furthermore, we quantify non-adiabatic corrections to the geometric phase by decreasing the manipulation time in order to optimize our geometric gate. Geometric phases have also been shown to be resilient against adiabatic field fluctuations. We are currently investigating the resilience of the geometric phases against noise in view of potential applications for quantum information processing and quantum metrology.
We have also studied the adiabatic geometric phase in another simple quantum system – a harmonic oscillator, naturally represented in our circuit QED setup as one of the electromagnetic modes of an on-chip coplanar waveguide resonator [3]. Unlike the qubit case, the geometric phase of a harmonic oscillator is a global phase common to all energy eigenstates and, as a result, is not directly observable. Therefore, we make use of a transmon-type qubit dispersively coupled to the resonator mode as a probe. The coupling modifies the oscillator geometric phase depending on the qubit state, which allows us to read out the phase difference in a standard interferometric measurement (Fig. 1b). We have observed the key features of the geometric phase – its dependence on the shape of the quantum state path only and its insensitivity to the total evolution time. We have also identified non-adiabatic effects which cause undesirable qubit-oscillator entanglement, resulting in qubit dephasing. However, the measured qubit coherence exhibits revivals when the total evolution time is approximately divisible by the period of the non-adiabatic transients. This points towards future implementations of faster, non-adiabatic geometric quantum gates which benefit from the expected noise resilience of geometric phases but do not suffer from decoherence due to non-adiabaticity.
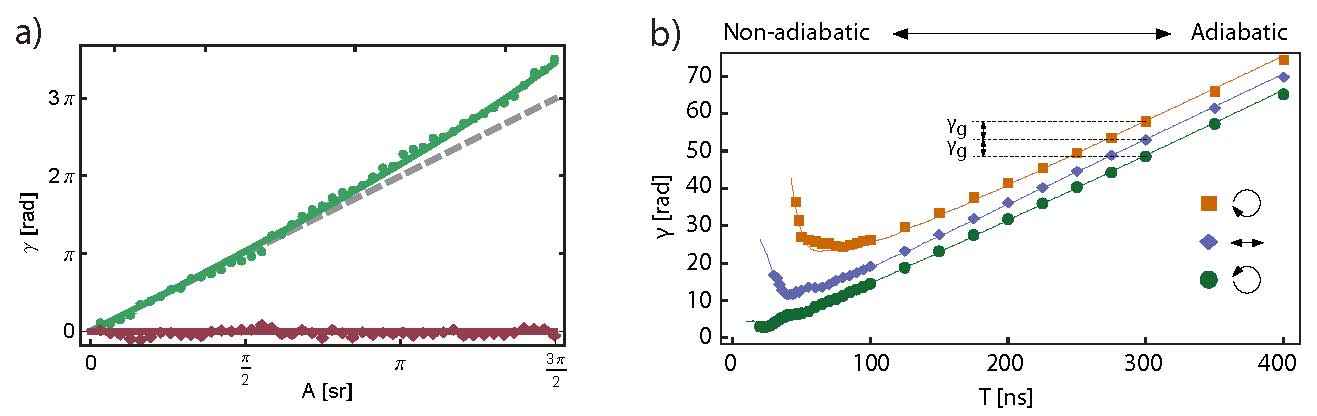
Figure 1(a) Experimentally determined geometric phase γ of a qubit as a function of the solid angle Α enclosed by the effective magnetic field applied to the qubit [2]. Shown is the data where geometric phase was acquired (green dots) as well as the zero phase measured in a control experiment (red diamonds). Theory curves obtained with secondorder perturbation theory (solid lines) and the prediction for a two-level system (dashed line) are also plotted. (b) The total measured phase γ accumulated by a harmonic oscillator as a function of the total evolution time T [3]. The geometric phase γg is determined by the difference between the trajectories encircling a positive (green), negative (orange) and zero (blue) area.
[1] Observation of Berry's Phase in a Solid-State Qubit Science 318, 1889 (2007)
[2] Geometric phases in superconducting qubits beyond the two-level-approximation, Physical Review B 85, 220502(R) (2012), also in arXiv:1204.1278
[3] Geometric Phase and Nonadiabatic Effects in an Electronic Harmonic Oscillator, Phys. Rev. Lett. 108, 170401 (2012), also in arXiv:1109.1157