Transferring the state of an information carrier between two parties is an essential primitive in both classical and quantum communication and information processing. Quantum teleportation describes the concept of transferring an unknown quantum state from a sender to a physically separated receiver without transmitting the physical carrier of information itself. Instead, teleportation makes use of the non-local correlations provided by an entangled pair shared between the sender and the receiver and the exchange of classical information. We have teleported information for the first time in a solid state system. In our chip-based superconducting circuit architecture we have realized the full deterministic quantum teleportation protocol using quantum-limited parametric amplifiers, a crossed quantum bus technology and flexible real-time digital electronics. The teleportation process succeeds with order unit probability for any input state, as we reliably prepare entangled states as a resource and are able to distinguish all four maximally entangled Bell states in a single measurement.

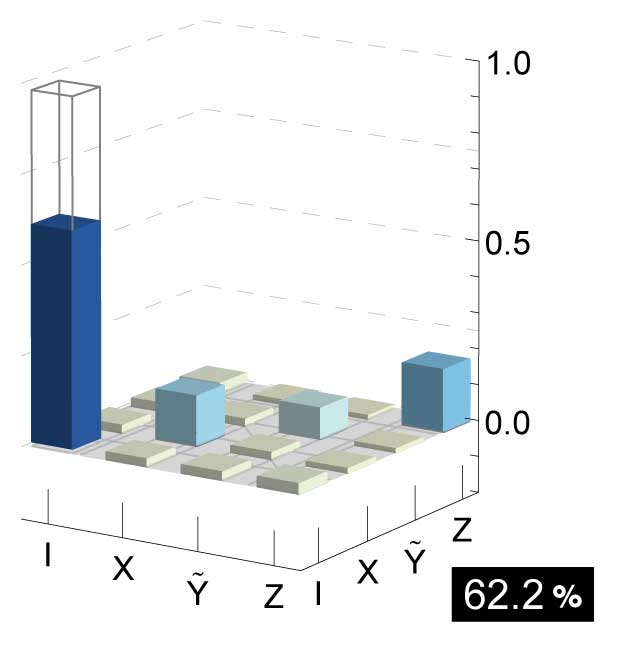Figure 2: The solid bars show the experimentally obtained process matrix describing the state transfer from the sender to the receiver. The ideal process matrix, which is the identity operation, is shown in wire frames. (large view)

The success of the teleportation protocol in every instance with unit fidelity is counterintuitive from a classical point of view. The receiver’s quantum bit (qubit) does not interact with any other qubit after it has been entangled with one of two qubits in the senders possession. The input state (|ψ_in⟩) is prepared afterwards at the other qubit of the sender. The classical information sent by the sender is not sufficient to recreate |ψ_in⟩ perfectly at the receiver. Indeed, assuming no entanglement between sender and receiver one can replicate the sender’s state at best with a process fidelity of 1/2. To always recover the original state |ψ_in⟩ the sender performs a measurement in the basis of the Bell states, which projects the two qubits in the sender’s possession randomly onto one of the four Bell states. As a consequence the receiver’s qubit is projected instantaneously into a state related to |ψ_in⟩ without ever having interacted with the senders qubit. The receiver’s qubit only differs from the input state by a single-qubit rotation which depends on the four possible measurement results. In the final step, the sender communicates the Bell measurement result as two bits of classical information via a classical channel and therefore the receiver can always obtain the original input state |ψ_in⟩. This final step is frequently referred to as feed-forward.

To identify simultaneously the four outcomes of the Bell-state measurement in a deterministic way we use two-qubit single-shot read-out for which we achieve a success probability of (81.8±0.5)%. In the teleportation protocol we analyze the Bell-state measurement in real time by using fast electronics based on a field programmable gate array (FPGA) and realize the feed-forward step in about 500 ns. We have achieved an average process fidelity of (62.2±0.3)% for the full quantum teleportation algorithm, which is clearly above the classical threshold (Fig. 2). We have demonstrated teleportation at a rate of 10,000 quantum bits per second between two macroscopic systems separated by 6 mm.

Full article:
http://www.nature.com/nature/journal/v500/n7462/full/nature12422.html?WT_ec_id=NATURE-20130815

ETH-Life article:
http://test-ethlife.ethz.ch/archive_articles/130815_teleportation_fb/index_EN

NZZ Campus video interview with Lars Steffen (in German):
http://campus.nzz.ch/video-casts/beam-me

More media articles and videos:
https://qudev.phys.ethz.ch/news
https://qudev.phys.ethz.ch/media